| 9. Ecuaciones diferenciales | 9.12. Soluciones de Fourier de ecuaciones diferenciales parciales | 9.12.1. La ecuación del calor |

Ejercicios propuestos para el Capítulo 9.12.1

1. Explique la Definición 9.12.1.2.
2. Explique la Definición 9.12.1.3.
3. Explique la Definición 9.12.1.4.

4. C Realizar experimentos numéricos con la solución formal obtenida en el Ejemplo 9.12.1.1.
5. C Realizar experimentos numéricos con la solución formal obtenida en el Ejemplo 9.12.1.2.
6. C Realizar experimentos numéricos con la solución formal obtenida en el Ejemplo 9.12.1.3.
7. C Realizar experimentos numéricos con la solución formal obtenida en el Ejemplo 9.12.1.4.

      En los ejercicios 8 a 42, resuelva el problema de valor inicial y de frontera. Donde esté indicado por C, realice experimentos numéricos. Para simplificar el cálculo de los coeficientes en algunos de estos problemas, compruebe primero si u(x, 0) es un polinomio que satisface las condiciones de contorno. Si lo hace, aplique el Teorema 9.11.3.5; también, vea los Ejercicios 9.11.3.35(b), 9.11.3.42(b), y 9.11.3.50(b).

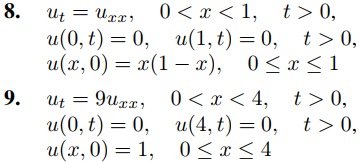
      En los ejercicios 43 a 46 resuelve el problema de valor inicial y de frontera. Realice experimentos numéricos para valores específicos de L y a.

47. Sea h continua en [0, L] y sean u₀, u_L y a constantes, con a > 0. Demuestre que siempre es posible encontrar una función q que satisfaga (a), (b) o ( c), pero que esto no es así para (d).

       

      En los Ejercicios 48 a 53 resuelva el problema de valor inicial y de frontera no homogéneo.

54. En este ejercicio se da por sentado que la serie infinita converge para todo p si q > 0, y, en su caso, utilizar la prueba de comparación para la convergencia absoluta de una serie infinita.

Sea

donde

y f es suave por tramos en [0, L].

      (a) Demuestre que u está definido para (x, t) tal que t > 0.

      (b) Para t > 0 fijo, utilice el Teorema 9.12.1.1 con z = x para demostrar que

       (c) Partiendo del resultado de (a), use el Teorema 9.12.1.1 con z = x para mostrar que, para un t > 0 fijo,

       (d) Para x fijo pero arbitrario, utilice el Teorema 9.12.1.1 con z = t para demostrar que

si t > t₀ > 0, donde t₀ es un número positivo arbitrario. Luego argumente que dado que t₀ es arbitrario, la conclusión se cumple para todo t > 0.

      (e) Concluya de (c) y (d) que

u_t = a2u_xx,  −∞ < x < ∞,  t > 0.

Al aplicar repetidamente los argumentos en (a) y (c), se puede demostrar que u puede diferenciarse término por término cualquier número de veces con respecto a x y/o t si t > 0.