| 11. Diferenciación de funciones de varias variables |

11.2 Límites y continuidad de una función multivariable

Objetivos de aprendizaje

• 9.2.1 Calcular el límite de una función de dos variables.
• 9.2.2 Aprender cómo una función de dos variables puede aproximarse a diferentes valores en un punto límite, dependiendo de la ruta de aproximación.
• 9.2.3 Enunciar las condiciones de continuidad de una función de dos variables.
• 9.2.4 Verificar la continuidad de una función de dos variables en un punto.
• 9.2.5 Calcular el límite de una función de tres o más variables y verificar la continuidad de la función en un punto.

      En la sección anterior hemos examinado funciones de más de una variable y hemos visto cómo graficarlas. En esta sección, vemos cómo tomar el límite de una función de más de una variable y qué significa que una función de más de una variable sea continua en un punto de su dominio. Resulta que estos conceptos tienen aspectos que simplemente no ocurren con funciones de una variable.

Límite de una función de dos variables

Recuerde de “El límite de una función“, la definición de un límite de una función de una variable:

Sea f (x) una función definida para todo x ≠ a en un intervalo abierto que contiene a. Sea L un número real. Entonces

si para todo ε > 0 existe un δ > 0, tal que si 0 < |x − a| < δ para todo x en el dominio de f, entonces

| f (x) − L| > ε.

Antes de que podamos adaptar esta definición para definir un límite de una función de dos variables, primero debemos ver cómo extender la idea de un intervalo abierto en una variable a un intervalo abierto en dos variables.

Definición. Disco abierto

Considere un punto (a, b) ∈ R². Un disco δ centrado en el punto (a, b) se define como un disco abierto de radio δ centrado en el punto (a, b), es decir,

{(x, y) ∈ R²∣(x − a)² + (y − b)² < δ²} 

como se muestra en el siguiente gráfico. ♦

La idea de un disco δ aparece en la definición del límite de una función de dos variables. Si δ es pequeño, entonces todos los puntos (x, y) en el disco δ están cerca de (a, b). Esto es completamente análogo a que x esté cerca de a en la definición de un límite de una función de una variable. En una dimensión, expresamos esta restricción como

a − δ < x < a + δ.

Definición. Límite de una función de dos variables

Sea f una función de dos variables, x e y. El límite de f (x, y) cuando (x, y) tiende a (a, b) es L, escrito

si para cada ε > 0 existe un δ > 0 suficientemente pequeño tal que para todos los puntos (x, y) en un disco δ alrededor de (a, b), excepto posiblemente para (a, b) mismo, el valor de f (x,y) no está a más de ε de L (Figura 11.2_2 ). Usando símbolos, escribimos lo siguiente: Para cualquier ε > 0, existe un número δ > 0 tal que

♦

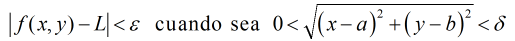Demostrar que existe un límite usando la definición de un límite de una función de dos variables puede ser un desafío. En cambio, usamos el siguiente teorema, que nos brinda atajos para encontrar límites. Las fórmulas de este teorema son una extensión de las fórmulas del teorema de las leyes de los límites en “Las leyes de los límites“.

Teorema 11.2.1: Leyes de límites para funciones de dos variables

Sean f (x, y) y g(x, y) dos funciones definidas para todo (x, y) ≠ (a, b) en una vecindad alrededor de (a, b), y supongamos que la vecindad está contenida completamente dentro del dominio de f . Suponga que L y M son números reales tales que lím_{(x, y)→(a, b)} f (x, y) = L  y  lím_{(x, y)→(a, b)}g(x, y) = M, y sea c una constante. Entonces cada una de las siguientes afirmaciones se cumple:

Propiedad de la constante:

lím_{(x, y)→(a, b)} c = c         (11.2.2)

Propiedades de identidad:

lím_{(x, y)→(a, b)} x = a                    (11.2.3)

lím_{(x, y)→(a, b)} y = b                    (11.2.4)

Propiedad de la suma:

lím_{(x, y)→(a, b)} (f (x,y) + g(x,y)) = L + M                   (11.2.5)

Propiedad de la diferencia:

lím_{(x, y)→(a, b)} (f (x,y) − g(x,y)) = L − M                   (11.2.6)

Propiedad del múltiplo constante:

lím_{(x, y)→(a, b)} (cf (x,y)) = cL                   (11.2.7)

Propiedad del producto:

lím_{(x, y)→(a, b)} (f (x,y) ⋅ g(x,y)) = L ⋅ M                   (11.2.8)

Propiedad del cociente:

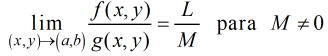                     (11.2.9)

Propiedad de la potencia:

lím_{(x, y)→(a, b)} (f (x,y))ⁿ = Lⁿ                  (11.2.10)

para cualquier entero positivo n.

Propiedad de la raíz:

                 (11.2.11)

para todo L si n es impar y positivo, y para  L ≥ 0 si n es par y positivo.  ♦

Las demostraciones de estas propiedades son similares a las de los límites de funciones de una variable. Podemos aplicar estas leyes para encontrar los límites de varias funciones.

Ejemplo ilustrativo 11.2.1  Encontrar el límite de una función de dos variables

Encuentre cada uno de los siguientes límites:

1. lím_{(x, y)→(2, −1)} (x² − 2xy + 3y² − 4x + 3y − 6)
2. lím_{(x, y)→(2, −1) (2x+3y)/(4x−3y)}

Solución:

a. Primero usa las leyes de la suma y la diferencia para separar los términos:

A continuación, utilice la ley del múltiplo constante en los límites segundo, tercero, cuarto y quinto:

Ahora, use la ley de potencia en el primer y tercer límite, y la ley del producto en el segundo límite:

Por último, use las leyes de identidad en los primeros seis límites y la ley constante en el último límite:

b. Antes de aplicar la ley del cociente, debemos verificar que el límite del denominador sea distinto de cero. Usando la ley de la diferencia, la ley del múltiplo constante y la ley de la identidad,

Como el límite del denominador es distinto de cero, se aplica la ley del cociente. Ahora calculamos el límite del numerador usando la ley de la diferencia, la ley del múltiplo constante y la ley de la identidad:

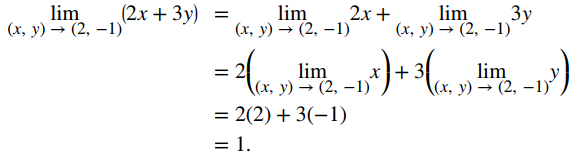
Por tanto, según la ley del cociente tenemos

♦

Ejercicio de control 11.2_1

Evalúe el siguiente límite:  ♦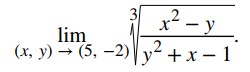

       Como estamos tomando el límite de una función de dos variables, el punto (a, b) está en R², y es posible acercarse a este punto desde un número infinito de direcciones. A veces, al calcular un límite, la respuesta varía según el camino que se tome hacia (a, b). Si este es el caso, entonces el límite no existe. En otras palabras, el límite debe ser único, independientemente del camino tomado.

Ejemplo ilustrativo 11.2.2 Límites que no existen

Demuestre que no existe ninguno de los siguientes límites:

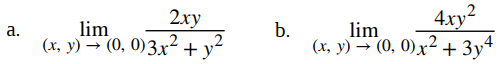
Solución:

a. El dominio de la función f (x, y) = 2xy/(3x² + y²) consta de todos los puntos en el plano xy excepto el punto (0,0) (Figura 11.2.3). Para mostrar que el límite no existe cuando (x, y) tiende a (0,0), notamos que es imposible satisfacer la definición de límite de una función de dos variables debido al hecho de que la función toma valores diferentes a lo largo de diferentes rectas que pasan por el punto (0,0). Primero, considere la recta y = 0 en el plano xy. Sustituyendo y = 0 en f (x, y) da

para cualquier valor de x. Por tanto, el valor de f permanece constante para cualquier punto del eje x, y cuando y tiende a cero, la función permanece fija en cero.

A continuación, considere la recta y = x. Sustituyendo y = x en f (x, y) da

Esto es cierto para cualquier punto de la recta y = x. Si dejamos que x se acerque a cero mientras permanecemos en esta recta, el valor de la función permanece fijo en 1/2, independientemente de cuán pequeño sea x.

Elija un valor para ε que sea menor que 1/2, por ejemplo, 1/4. Entonces, no importa cuán pequeño sea el disco δ que dibujemos alrededor de (0,0), los valores de f (x, y) para los puntos dentro de ese disco δ incluirán tanto 0 como 1/2. Por lo tanto, la definición de límite en un punto es nunca satisfecho y el límite no existe.

b. De manera similar que en el apartado a., podemos acercarnos al origen a lo largo de cualquier línea recta que pase por el origen. Si probamos el eje x (es decir, y = 0), entonces la función permanece fija en cero. Lo mismo es cierto para el eje y. Supongamos que nos acercamos al origen a lo largo de una línea recta de pendiente k. La ecuación de esta recta es y = kx. Entonces el límite se convierte en

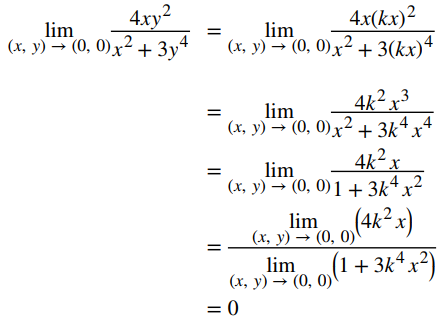
independientemente del valor de k. Parecería que el límite es igual a cero. ¿Qué pasa si en su lugar elegimos una curva que pasa por el origen? Por ejemplo, podemos considerar la parábola dada por la ecuación x = y². Sustituyendo y² en lugar de x en f (x, y) da

Por la misma lógica que en el aparatado a., es imposible encontrar un disco δ alrededor del origen que satisfaga la definición del límite para cualquier valor de ε < 1. Por lo tanto, 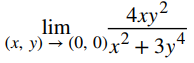no existe.  ♦

Ejercicio de control 11.2_2

Muestre que no existe.  ♦