| 11. Diferenciación de funciones de varias variables | 11.2 Límites y continuidad de una función multivariable |

Puntos interiores y puntos de contorno de un subconjunto de R²

Para estudiar la continuidad y diferenciabilidad de una función de dos o más variables, primero debemos aprender alguna terminología nueva.

Definición. Punto interior y punto de frontera de un subconjunto de R²

Sea S un subconjunto de R² (Figura 11.2_4).

1. Un punto P₀ se llama punto interior de S si hay un disco δ centrado alrededor de P₀ contenido completamente en S.
2. Un punto P₀ se llama punto de frontera (o punto de contorno) de S si cada disco δ centrado alrededor de P₀ contiene puntos tanto dentro como fuera de S.

Definición. Conjunto abierto y conjunto cerrado

Sea S un subconjunto de R² (Figura 11.2_4).

1. S se llama conjunto abierto si todo punto de S es un punto interior.
2. S se llama conjunto cerrado si contiene todos sus puntos límite.

Un ejemplo de un conjunto abierto es un disco δ. Si incluimos la frontera del disco, entonces se convierte en un conjunto cerrado. Un conjunto que contiene algunos de sus puntos de contorno, pero no todos, no es ni abierto ni cerrado. Por ejemplo, si incluimos la mitad de la frontera de un disco δ pero no la otra mitad, entonces el conjunto no es ni abierto ni cerrado.

Definición. Conjunto conexo y región

Sea S un subconjunto de R² (Figura 11.2_4).

1. Un conjunto abierto S es un conjunto conexo si no puede representarse como la unión de dos o más subconjuntos abiertos disjuntos y no vacíos.
2. Un conjunto S es una región si es abierto, conexo y no vacío.

La definición de límite de una función de dos variables requiere que el disco δ esté contenido dentro del dominio de la función. Sin embargo, si deseamos encontrar el límite de una función en un punto límite del dominio, el disco δ no está contenido dentro del dominio. Por definición, algunos de los puntos del disco δ están dentro del dominio y otros están fuera. Por lo tanto, solo necesitamos considerar los puntos que están dentro del disco δ y del dominio de la función. Esto conduce a la definición del límite de una función en un punto límite.

DEFINICIÓN:  Límite de una función en un punto límite.

Sea f una función de dos variables, x e y, y supongamos que (a, b) está en la frontera del dominio de f. Entonces, el límite de f (x, y) cuando (x, y) tiende a (a, b) es L, escrito

si para cualquier ε > 0, existe un número δ > 0 tal que para cualquier punto (x, y) dentro del dominio de f y dentro de una distancia adecuadamente pequeña positiva δ de (a, b), el valor de f (x, y) no está a más de ε de L (Figura 11.2.2). Usando símbolos, podemos escribir: Para cualquier ε > 0, existe un número δ > 0 tal que

♦

Ejemplo ilustrativo 11.2.3  Límite de una función en un punto de frontera

Pruebe que

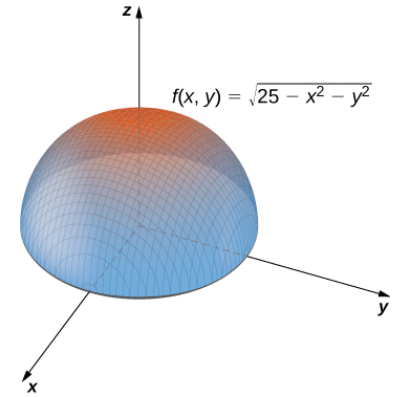
Solución:  Figura 11.2_5 Dominio de la función f (x, y) = √(25 − x² − y²).

El dominio de la función   es que es una circunferencia de radio 5 con centro en el origen, junto con su interior como se muestra en la siguiente gráfica.

Podemos usar las leyes de los límites, que se aplican a los límites en la frontera de los dominios así como a los puntos interiores:

Vea el siguiente gráfico.

Ejercicio de control 11.2_3

Evalúe el siguiente límite:

Continuidad de funciones de dos variables

En “Continuidad“, definimos la continuidad de una función de una variable y vimos cómo dependía del límite de una función de una variable. En particular, son necesarias tres condiciones para que f (x) sea continua en el punto x = a:

Estas tres condiciones también son necesarias para la continuidad de una función de dos variables.

DEFINICIÓN

Una función f (x, y) es continua en un punto (a, b) de su dominio si se cumplen las siguientes condiciones:

♦

Ejemplo ilustrativo 11.2.4 Demostración de la continuidad de una función de dos variables