| Álgebra lineal con aplicaciones | 3. Determinantes y Diagonalización |

3.1 La expansión del cofactor

       En la Sección 2.4 definimos el determinante de una matriz de 2×2 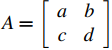como sigue (Los determinantes se escriben comúnmente |A| = det A usando barras verticales. Usaremos ambas notaciones.):

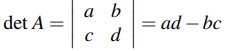
y mostró (en el ejemplo 2.4.4) que A tiene una inversa si y solo si det A ≠ 0. Un objetivo de este capítulo es hacer esto para cualquier matriz cuadrada A. No hay dificultad para matrices 1 × 1: Si A = [a], definimos det A = det [a] = a y observe que A es invertible si y solo si a ≠ 0.

      Si A es 3×3 e invertible, buscamos una definición adecuada de det A tratando de llevar A a la matriz identidad mediante operaciones de fila. La primera columna no es cero (A es invertible); supongamos que la entrada a ≠ 0. Entonces las operaciones de fila dan

donde u = ae − bd  y  v = ah − bg. Como A es invertible, uno de u y v es distinto de cero (por el ejemplo 2.4.11); supongamos que u ≠ 0. Entonces procede la reducción