| 2. Límites y continuidad | 2.1 Una vista previa del cálculo |

Ejercicios resueltos del capítulo 2.1

    En los problemas 1-14, trace la gráfica de la función para encontrar el límite dado, o concluya que no existe.

Zill 2.1_3   lím_x→0(1 + 1/x)

Solución – Juan Beltrán:

Sea la función f (x) = 1 + 1/x, dom f =  R − {0}

♦  f (0) no existe: No hay cortes con el eje y

♦  1 + 1/x = 0 ⇒ (x + 1)/x = 0 ⇒ x = –1: Corte con el eje x

♦  Cuando x toma valores cada vez más grandes (o cada vez más pequeños), 1/x → 0 y f (x) = 1 + 1/x → 1; y = 1: Asíntota horizontal. Observa la siguiente tabla.

x	–10	–100	–1000	–10000	10	100	1000	10000
f (x)	0.900000	0.990000	0.999000	0.999900	1.100000	1.010000	1.001000	1.000100

♦  Cuando x toma valores cada vez más cercanos a 0 pero menores que 0, 1/x tiende a −∞  y  f (x) = 1 + 1/x → −∞. Lo mismo, Cuando x toma valores cada vez más cercanos a 0 pero mayores que 0, 1/x tiende a +∞  y  f (x) = 1 + 1/x → +∞. x = 0: Asíntota vertical.Observa la siguiente tabla.

x	−0.1	−0.01	−0.001	−0.0001	0.0001	0.001	0.01	0.1
f (x)	−9	-99	-999	-99999	10001	1001	101	11

Teniendo presente los datos anteriores es posible trazar de una manera precisa la gráfica de la función f (x) = 1 + 1/x

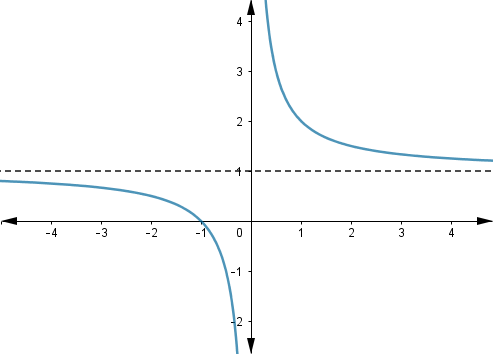
Como lim_x→0⁻ f (x) = −∞  y  lim_x→0⁺ f (x) = ∞, se concluye que lim_x→0 f (x) No existe.

Zill 2.1_6   lím_x→0(x² − 3x)/x

Solución – Juan Beltrán:

Sea la función f (x) = (x² − 3x)/x, dom f =  R − {0}

Como (x² − 3x)/x = x(x − 3)/x = x − 3, x ≠ 0; podemos reescribir la función como:

f (x) = x − 3, dom f =  R − {0}

La gráfica de esta función lineal, con forma canónica y = mx + b, es una recta con:

    •  m = 1 > 0: Pendiente positiva (creciente).

    •  b = −3 : Ordenada al origen.

    •  x − 3 = 0 ⇒ x = 3: corte con el eje x.

    •  La gráfica presenta un “hueco” en el punto (0, −3).

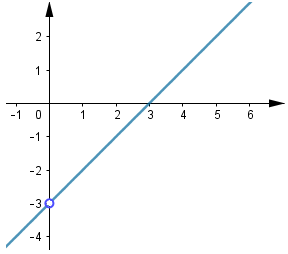
En la gráfica se observa que lim_x→0⁻ f (x) = −3  y  lim_x→0⁺ f (x) = −3, por lo que se infiere gráficamente que lim_x→0 f (x) = −3.

Zill 2.1_10   lím_x→1(x⁴ − 1)/(x² − 1)

Solución – Juan Beltrán:

Sea la función f (x) = (x⁴ − 1)/(x² − 1), dom f =  R − {-1, 1}

Debido a que (x² − 1)(x² + 1)/(x² − 1) = (x² + 1), x ≠ ±1; podemos reescribir la función como:

f (x) = x² + 1, dom f =  R − {-1, 1}

La gráfica de esta función cuadrática, con forma general y = ax² + bx + c, es una parábola con:

    •  a = 1 > 0: Abre hacia arriba.

    •  b = 0; −b/2a = 0: Abscisa del vértice y f (0) = 1: Ordenada del vértice.

    •  c = 1: Corte con el eje y.

    •  x² + 1 ≠ 0 ∀x∈R : No hay cortes con el eje x.

    •  f tiene dos huecos en los puntos (1, 2) y (−1, 2).

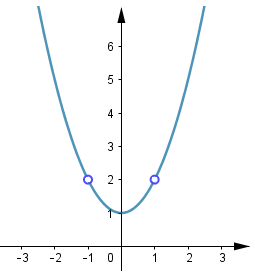
En la gráfica se observa que lim_x→1⁻ f (x) = 2  y  lim_x→1⁺ f (x) = 2, por lo que se infiere gráficamente que lim_x→1 f (x) = 2.