| 10. Cálculo vectorial – Vectores en el espacio | 10.6 Superficies cuadráticas |

Ejercicios propuestos para el Capítulo 10.6

Para los siguientes ejercicios, trace y describa la superficie cilíndrica de la ecuación dada.

303. [T] $x^2 + z^2 = 1$

304. [T] $x^2 + y^2 = 9$

305. [T] $z = \cos \left( \frac{\pi}{2} + x \right)$

306. [T] $z = e^x$

307. [T] $z = 9 – y^2$

308. [T] $z = \ln (x)$

Para los siguientes ejercicios, se da la gráfica de una superficie cuádrica.

1. Especifique el nombre de la superficie cuádrica.
2. Determine el eje de la superficie cuádrica.

309.

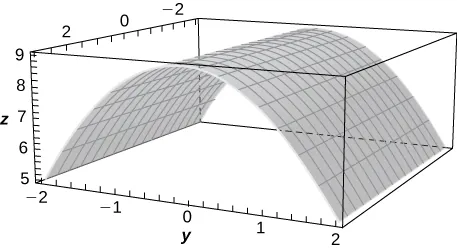
310.

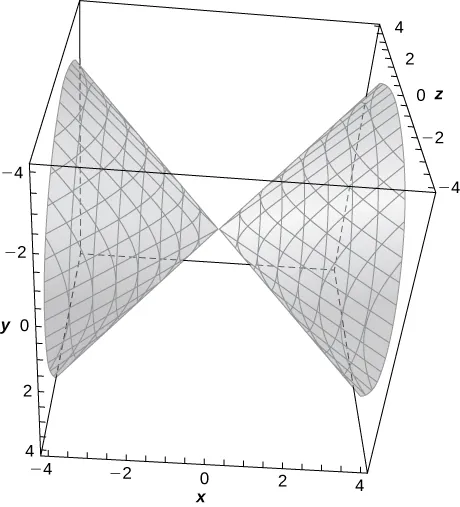
311.

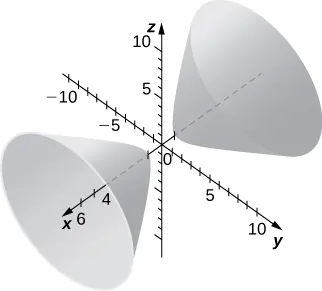
312.

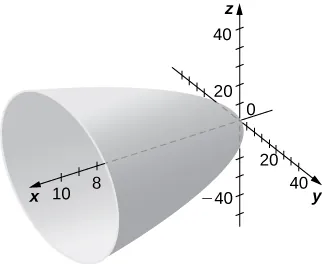
Para los siguientes ejercicios, relacione la superficie cuádrica dada con su ecuación correspondiente en forma estándar.

313. Hiperboloide de dos hojas

314. Elipsoide

315. Paraboloide elíptico

316. Paraboloide hiperbólico

317. Hiperboloide de una hoja

318. Cono elíptico

Para los siguientes ejercicios, reescriba la ecuación dada de la superficie cuádrica en su forma estándar e identifique la superficie.

319. $-x^2 + 36y^2 + 36z^2 = 9$

320. $-4x^2 + 25y^2 + z^2 = 100$

321. $-3x^2 + 5y^2 – z^2 = 10$

322. $3x^2 – y^2 – 6z^2 = 18$

323. $5y = x^2 – z^2$

324. $8x^2 – 5y^2 – 10z = 0$

325. $x^2 + 5y^2 + 3z^2 – 15 = 0$

326. $63x^2 + 7y^2 + 9z^2 – 63 = 0$

327. $x^2 + 5y^2 – 8z^2 = 0$

328. $5x^2 – 4y^2 + 20z^2 = 0$

329. $6x = 3y^2 + 2z^2$

330. $49y = x^2 + 7z^2$

Para los siguientes ejercicios, encuentre la traza de la superficie cuádrica dada en el plano de coordenadas especificado y trácela.

331. [T] $x^2 + z^2 + 4y = 0, z = 0$

332. [T] $x^2 + z^2 + 4y = 0, x = 0$

333. [T] $-4x^2 + 25y^2 + z^2 = 100, x = 0$

334. [T] $-4x^2 + 25y^2 + z^2 = 100, y = 0$

335. [T] $x^2 + \frac{y^2}{4} + \frac{z^2}{100} = 1, x = 0$

336. [T] $x^2 – y – z^2 = 1, y = 0$

337. Utilice la gráfica de la superficie cuádrica dada para responder a las preguntas.

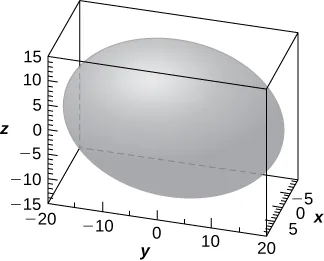
1. Especifique el nombre de la superficie cuádrica.
2. ¿Cuál de las ecuaciones $-16x^2 + 9y^2 + 36z^2 = 3600$, $9x^2 + 36y^2 + 16z^2 = 3600$, o $36x^2 + 9y^2 + 16z^2 = 3600$ corresponde a la gráfica?
3. Utilice el inciso b. para escribir la ecuación de la superficie cuádrica en su forma estándar.

338. Utiliza la gráfica de la superficie cuádrica dada para responder las preguntas.

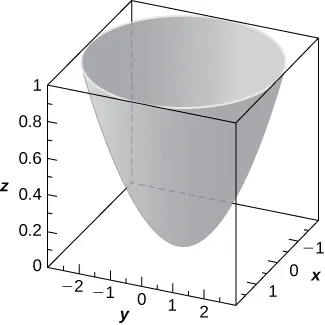
1. Especifique el nombre de la superficie cuádrica.
2. ¿Cuál de las ecuaciones $-36z = 9x^2 + y^2$, $9x^2 + 4y^2 = 36z$, o $-36z = -81x^2 + 4y^2$ corresponde a la gráfica de arriba?
3. Utilice el inciso b. para escribir la ecuación de la superficie cuádrica en su forma estándar.

Para los siguientes ejercicios, se da la ecuación de una superficie cuádrica.

1. Utilice el método de completar el cuadrado para escribir la ecuación en su forma estándar.
2. Identifique la superficie.

339. $x^2 + 2z^2 + 6x – 8z + 1 = 0$

340. $4x^2 – y^2 + z^2 – 8x + 2y + 2z + 3 = 0$

341. $x^2 + 4y^2 – 4z^2 – 6x – 16y – 16z + 5 = 0$

342. $x^2 + z^2 – 4y + 4 = 0$

343. $x^2 + \frac{y^2}{4} – \frac{z^2}{3} + 6x + 9 = 0$

344. $x^2 – y^2 + z^2 – 12z + 2x + 37 = 0$

345. Escriba la forma estándar de la ecuación del elipsoide centrado en el origen que pasa por los puntos $A(2,0,0)$, $B(0,0,1)$ y $C\left( \frac{1}{2}, \sqrt{11}, \frac{1}{2} \right)$.

346. Escriba la forma estándar de la ecuación del elipsoide centrado en el punto $P(1,1,0)$ que pasa por los puntos $A(6,1,0)$, $B(4,2,0)$ y $C(1,2,1)$.

347. Determine los puntos de intersección del cono elíptico $x^2 – y^2 – z^2 = 0$ con la recta de ecuaciones simétricas $\frac{x-1}{2} = \frac{y+1}{3} = z$.

348. Determine los puntos de intersección del paraboloide hiperbólico $z = 3x^2 – 2y^2$ con la recta de ecuaciones paramétricas $x = 3t, y = 2t, z = 19t$, donde $t \in \mathbb{R}$.

349. Encuentre la ecuación de la superficie cuádrica con puntos $P(x,y,z)$ que son equidistantes del punto $Q(0,-1,0)$ y del plano de ecuación $y = 1$. Identifique la superficie.

350. Encuentre la ecuación de la superficie cuádrica con puntos $P(x,y,z)$ que son equidistantes del punto $Q(0,2,0)$ y del plano de ecuación $y = -2$. Identifique la superficie.

351. Si la superficie de un reflector parabólico se describe mediante la ecuación $400z = x^2 + y^2$, encuentre el punto focal del reflector.

352. Considere el reflector parabólico descrito por la ecuación $z = 20x^2 + 20y^2$. Encuentre su punto focal.

353. Demuestre que la superficie cuádrica $x^2 + y^2 + z^2 + 2xy + 2xz + 2yz + x + y + z = 0$ se reduce a dos planos paralelos.

354. Demuestre que la superficie cuádrica $x^2 + y^2 + z^2 – 2xy – 2xz + 2yz – 1 = 0$ se reduce a dos planos paralelos que pasan.

355. [T] La intersección entre el cilindro $(x-1)^2 + y^2 = 1$ y la esfera $x^2 + y^2 + z^2 = 4$ se llama

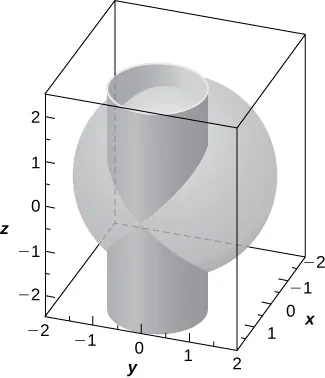
1. Resuelva el sistema conformado por las ecuaciones de las superficies para encontrar las ecuaciones de la curva de intersección. (Sugerencia: Encuentre $x$ e $y$ en términos de $z$.)
2. Utilice un sistema de álgebra computacional (CAS) para visualizar la curva de intersección en la esfera $x^2 + y^2 + z^2 = 4$.

356. Un hiperboloide de una hoja $25x^2 + 25y^2 – z^2 = 25$ y un cono elíptico $-25x^2 + 75y^2 + z^2 = 0$ se representan en la siguiente figura junto con sus curvas de intersección. Identifique las curvas de intersección y encuentre sus ecuaciones (Sugerencia: Encuentre $y$ a partir del sistema conformado por las ecuaciones de las superficies).

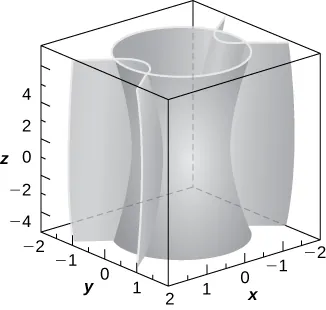
357. [T] Utilice un CAS para crear la intersección entre el cilindro $9x^2 + 4y^2 = 18$ y el elipsoide $36x^2 + 16y^2 + 9z^2 = 144$, y encuentre las ecuaciones de las curvas de intersección.

358. [T] Un esferoide es un elipsoide con dos semiejes iguales. Por ejemplo, la ecuación de un esferoide con el eje $z$ como su eje de simetría viene dada por $\frac{x^2}{a^2} + \frac{y^2}{a^2} + \frac{z^2}{c^2} = 1$, donde $a$ y $c$ son números reales positivos. El esferoide se llama oblate (achatado) si $c < a$, y prolate (alargado) para $c > a$.

359. [T] En cartografía, la Tierra se aproxima mediante un esferoide achatado en lugar de una esfera. Los radios en el ecuador y los polos son aproximadamente $3963 \text{ mi}$ y $3950 \text{ mi}$, respectivamente.

360. [T] Un juego de imanes acrobáticos zumbadores (o “huevos de cascabel”) incluye dos imanes brillantes, pulidos y superfuertes con forma de esferoide, muy conocidos para el entretenimiento infantil. Cada imán mide $1.625 \text{ pulg.}$ de largo y $0.5 \text{ pulg.}$ de ancho en el centro. Mientras se lanzan al aire, crean un sonido de zumbido mientras se atraen entre sí.

361. [T] Una superficie con forma de corazón está dada por la ecuación $\left(x^2 + \frac{9}{4}y^2 + z^2 – 1\right)^3 – x^2z^3 – \frac{9}{80}y^2z^3 = 0$.

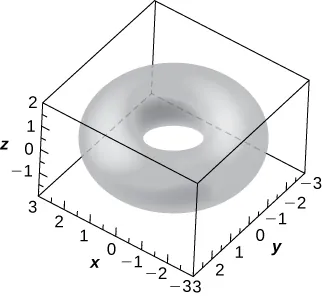
362. [T] El toro circular simétrico respecto al eje $z$ es un tipo especial de superficie en topología y su ecuación viene dada por $\left(x^2 + y^2 + z^2 + R^2 – r^2\right)^2 = 4R^2(x^2 + y^2)$, donde $R > r > 0$. Los números $R$ y $r$ se llaman los radios mayor y menor, respectivamente, de la superficie. La siguiente figura muestra un toro circular para el cual $R = 2$ y $r = 1$.