| 7. Sucesiones y series infinitas | 7.1 Sucesiones |

Ejercicios propuestos para el Capítulo 7.1

       Encuentre los primeros seis términos de cada una de las siguientes secuencias (1 a 4), comenzando con n = 1:

1. a_n = 1 + (−1)ⁿ  para  n ≥ 1

Ver la solución

2. a_n = n² − 1  para  n ≥ 1

3. a₁ = 1  y  a_n = a_{n − 1} + n  para  n ≥ 2

4. a₁ = 1, a₂ = 1  y  a_{n + 2} = a_n + a_{n + 1}  para  n ≥ 1.

Ver la solución

5. Encuentre una fórmula explícita para a_n donde a₁ = 1  y  a_{n − 1} + n  para  n ≥ 2.

Ver la solución

6. Encuentre una fórmula a_n para el enésimo término de la secuencia aritmética cuyo primer término es a₁ = 1 tal que a_{n + 1} − a_n = 17 para n ≥ 1.

7. Encuentre una fórmula a_n para el enésimo término de la secuencia aritmética cuyo primer término es a₁ = −3 tal que a_{n + 1} − a_n = 4 para n ≥ 1.

Ver la solución

8. Encuentre una fórmula a_n para el enésimo término de la secuencia geométrica cuyo primer término es a₁ = 1 tal que a_{n + 1}/a_n = 10 para n ≥ 1.

Ver la solución

9. Encuentre una fórmula a_n para el enésimo término de la secuencia geométrica cuyo primer término es a₁ = 3 tal que a_{n + 1}/a_n = 1/10 para n ≥ 1.

10. Encuentre una fórmula explícita para el enésimo término de la secuencia cuyos primeros términos son {0, 3, 8, 15, 24, 35, 48, 63, 80, 99,…}. (Sugerencia: primero agregue uno a cada término).

Ver la solución

11. Encuentre una fórmula explícita para el enésimo término de la secuencia que satisfaga a₁ = 0  y a_n= 2a_{n − 1}  + 1 para n ≥ 2.

 

      Encuentre una fórmula para el término general a_n de cada una de las siguientes secuencias:

12. {1, 0, −1, 0, 1, 0, −1, 0,…} (Sugerencia: encuentre dónde senx toma estos valores)

13. {1, −1/3, 1/5, −1/7, …}.

Ver la solución

 

      Encuentre una función f (n) que identifique el enésimo término a_n de las siguientes secuencias definidas recursivamente, como a_n = f (n): 

14. a₁ = 1 y a_{n + 1} = −a_n para n ≥ 1

Ver la solución

15. a₁ = 2 y a_{n + 1} = 2a_n para n ≥ 1

16. a₁ = 1 y a_{n + 1} = (n + 1)a_n para n ≥ 1

17. a₁ = 2 y a_{n + 1} = (n + 1)a_n/2 para n ≥ 1

18. a₁ = 1 y a_{n + 1} = a_n/2ⁿ para n ≥ 1.

Ver la solución

 

      Grafique los primeros N términos de cada secuencia. Indique si la evidencia gráfica sugiere que la secuencia converge o diverge:

19. [T]  a₁ = 1, a₂ = 2, y para n ≥ 2, a_n = (a_{n − 1} + a_{n − 2})/2; N = 30

20. [T]  a₁ = 1, a₂ = 2, a₃ = 3 y para n ≥ 4, a_n = (a_{n − 1} + a_{n − 2}  + a_{n − 3})/3, N = 30

21. [T]  a₁ = 1, a₂ = 2, y para n ≥ 3, a_n = √(a_{n − 1} a_{n − 2}); N = 30

22. [T]  a₁ = 1, a₂ = 2, a₃ = 3, y para n ≥ 4, a_n = √(a_{n − 1} a_{n − 2} a_{n − 3}); N = 30.

 

Suponga que lim_{n → ∞} a_n = 1, lim_{n → ∞} b_n = −1 y 0 <−b_n < a_n para todo n. Evalúe cada uno de los siguientes límites, o indique que el límite no existe, o indique que no hay suficiente información para determinar si el límite existe:

23. lim_{n → ∞} (3a_n − 4b_n)

24. lim_{n → ∞} ((1/2)b_n − (1/2)a_n)

25. lim_{n → ∞} (a_n + b_n)/(a_n − b_n)

Ver la solución

26. lim_{n → ∞} (a_n − b_n)/(a_n + b_n).

Encuentre el límite de cada una de las siguientes secuencias, usando la regla de L’Hôpital cuando sea apropiado.

Ver la solución

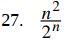
   Pista: 

Ver la solución

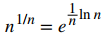
       Para cada una de las siguientes secuencias, cuyos términos enésimos están dados, indique si la secuencia está acotada y si eventualmente es monótona, creciente o decreciente.

Ver la solución

33.  senn

34.  cosn²

35.  n^1/n,  n ≥ 3

36.  n^−1/n,  n ≥ 3

37.  tann

38.  Determine si la secuencia definida a continuación tiene un límite. Si es así, encuentre el límite.

39.  Determine si la secuencia definida a continuación tiene un límite. Si es así, encuentre el límite.

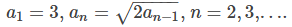
Usa el teorema de compresión para encontrar el límite de cada una de las siguientes secuencias.

40.  n sen(1/n)

43.  a_n = senn sen(1/n)

Para las siguientes sucesiones, grafique los primeros 25 términos de la secuencia e indique si la evidencia gráfica sugiere que la sucesión converge o diverge.

44. [T]  a_n = senn

45. [T]  a_n = cosn

Determine el límite de la secuencia o demuestre que la sucesión diverge. Si converge, encuentra su límite.

46.  a_n = tan⁻¹(n²)

47.  a_n = (2n)^1/n − n^1/n

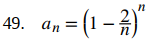
El método de Newton busca aproximar una solución f (x) = 0 que comienza con una aproximación inicial x₀ y define sucesivamente una secuencia Para la elección dada de  f  y x₀, describe la fórmula para x_{n + 1}. Si la secuencia parece converger, dé una fórmula exacta para la solución x, luego identifique el límite x con una precisión de cuatro lugares decimales y el n más pequeño de manera que x_n concuerde con x hasta cuatro lugares decimales.

54. [T]  f (x) = x² − 2, x₀ = 1

55. [T]  f (x) = (x − 1)² − 2, x₀ = 2

56. [T]  f (x) = e^x − 2, x₀ = 1

57. [T]  f (x) = ln x − 1, x₀ = 2

58. [T]  Suponga que comienza con un litro de vinagre y extrae repetidamente 0.1L, reemplaza con agua, mezcla y repite.
a. Encuentre una fórmula para la concentración después de n pasos.
b. ¿Después de cuántos pasos la mezcla contiene menos del 10% de vinagre?

59. [T] Un lago contiene inicialmente 2000 peces. Suponga que en ausencia de depredadores u otras causas de eliminación, la población de peces aumenta en un 6% cada mes. Sin embargo, teniendo en cuenta todas las causas adversas, se pierden 150 peces cada mes.
a. Explique por qué la población de peces después de n meses se modela con Pn = 1.06P_{n − 1} − 150 con P₀ = 2000.
b. ¿Cuántos peces habrá en el estanque después de un año?

60. [T]  Una cuenta bancaria gana 5% de interés compuesto mensualmente. Suponga que inicialmente se depositan $1000enlacuenta,peroqueseretiran$
$1000 en la cuenta, pero que se retiran$
10 cada mes.
a. Muestre que la cantidad en la cuenta después de n meses es A_n = (1 + .05/12) A_{n − 1} − 10; A₀ = 1000.
b. ¿Cuánto dinero habrá en la cuenta después de 1 año?
c. ¿La cantidad de dinero aumenta o disminuye?
d. Suponga que en lugar de $10, se retira una cantidad d fija de dólares cada mes. Encuentre un valor de d tal que la cantidad en la cuenta después de cada mes siga siendo $1000.
e. ¿Qué sucede si d es mayor que esta cantidad?

61. [T]  Un estudiante obtiene un préstamo universitario de $10,000aunatasadeinterésanualdel6$
$10,000 a una tasa de interés anual del 6%, compuesto mensualmente. a. Si el estudiante hace pagos de$
100 por mes, ¿cuánto debe el estudiante después de 12 meses?
b. ¿Después de cuántos meses se cancelará el préstamo?

62. [T]  Considere una serie que combina crecimiento geométrico y disminución aritmética. Sea a₁ = 1. Tome a > 1 y 0 < b < a. Establezca a_{n + 1} = a⋅a_n − b. Encuentre una fórmula para a_{n + 1} en términos de a_n, a y b y una relación entre a y b tal que a converja.

63. [T]  La representación binaria x = 0.b₁b₂b₃ … de un número x entre 0 y 1 se puede definir de la siguiente manera. Sea b₁ = 0 si x < 1/2 y b₁ = 1 si 1/2 ≤ x < 1. Sea x₁ = 2x − b₁. Sea b₂ = 0 si x₁ < 1/2 y b₂ = 1 si 1/2 ≤ x < 1. Sea x₂ = 2x₁ − b₂ y, en general, x_n = 2x_{n − 1} − b_n y b_{n − 1} = 0 si x_n <1/2 y b_{n − 1} = 1 si 1/2 ≤ x_n < 1. Encuentra la expansión binaria de 1/3.

64. [T]  Para encontrar una aproximación para π, establezca a₀ = √(2 + 1), a₁ = √(2 + a₀) y, en general, a_{n + 1} = √(2 + a_n). Finalmente, establezca p_n = √(3.2n² − a_n). Encuentre los primeros diez términos de p_n y compare los valores con π.

       Para los siguientes dos ejercicios, suponga que tiene acceso a un programa de computadora o fuente de Internet que puede generar una lista de ceros y unos de cualquier longitud deseada. Los generadores de números pseudoaleatorios (PRNG) juegan un papel importante en la simulación de ruido aleatorio en sistemas físicos al crear secuencias de ceros y unos que parecen el resultado de lanzar una moneda al aire repetidamente. Uno de los tipos más simples de PRNG define recursivamente una secuencia de N números enteros a₁, a₂, …, a_N de apariencia aleatoria fijando dos enteros especiales K y M y dejando que a_{n + 1} sea el resto después de dividir K.a_n en M, luego crea una secuencia de bits de ceros y unos cuyo enésimo término b_n es igual a uno si a_n es impar e igual a cero si a_n es par. Si los bits b_n son pseudoaleatorios, entonces el comportamiento de su promedio (b₁ + b₂ + ⋯ + b_N) / N debería ser similar al comportamiento de los promedios de bits generados verdaderamente al azar.

65. [T]  Comenzando con K = 16.807 y M = 2.147.483.647, usando diez valores iniciales diferentes de a1, calcule secuencias de bits b_n hasta n = 1000 y compare sus promedios con diez de tales secuencias generadas por un generador de bits aleatorio.

66. [T]  Encuentra los primeros 1000 dígitos de π usando un programa de computadora o un recurso de Internet. Cree una secuencia de bits b_n dejando b_n = 1 si el n-ésimo dígito de π es impar y b_n = 0 si el n-ésimo dígito de π es par. Calcule el valor promedio de b_n y el valor promedio de d_n = |b_{n + 1} − b_n|, n = 1, …, 999. ¿La secuencia b_n parece aleatoria? ¿Las diferencias entre los elementos sucesivos de b_n parecen aleatorias?