| 7. Sucesiones y series infinitas | Ejercicios propuestos para el Capítulo 7.1 |
7.1 SUCESIONES
Objetivos de aprendizaje:
7.1.1. Encontrar la fórmula para el término general de una sucesión.
7.1.2. Calcular el límite de una sucesión si existe.
7.1.3. Determinar la convergencia o divergencia de una sucesión dada.
En esta sección, presentamos sucesiones (secuencias) y definimos lo que significa que una secuencia converja o diverja. Mostramos cómo encontrar límites de secuencias que convergen, a menudo utilizando las propiedades de límites para las funciones de variable real discutidas anteriormente. Cerramos esta sección con el Teorema de la convergencia monótona, una herramienta que podemos usar para demostrar que ciertos tipos de sucesiones convergen.
Terminología de sucesiones
Para comenzar a trabajar con este nuevo tema, necesitamos algunos conceptos y definiciones. Primero, una sucesión infinita es una lista ordenada de números de la forma

Cada uno de los números en la sucesión se denomina término. El símbolo n se llama índice variable para la sucesión. Usamos la notación

para denotar esta sucesión. Se utiliza una notación similar para los conjuntos, pero una sucesión es una lista ordenada, mientras que un conjunto no necesariamente está ordenado. Debido a que existe un número particular a para cada entero positivo n, también podemos definir una sucesión como una función cuyo dominio es el conjunto de enteros positivos.
Consideremos la lista ordenada infinita
2, 4, 8, 16, 32, …
Esta es una sucesión en la que los términos primero, segundo y tercero están dados por a1 = 2, a2 = 4 y a3 = 8. Probablemente pueda ver que los términos en la sucesión tienen el siguiente patrón:
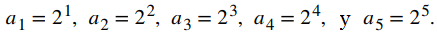
Suponiendo que este patrón continúa, podemos escribir el enésimo término en la sucesión mediante la fórmula explícita
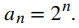
Usando la fórmula anterior, escribimos la secuencia como
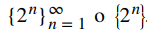
Alternativamente, se puede describir esta sucesión de una manera diferente. Como cada término es dos veces el término anterior, la sucesión se puede definir de forma recursiva expresando el enésimo término an en función del término anterior an − 1. En particular, podemos definir esta secuencia como la sucesión { an } donde a1 = 2 y para todo n ≥ 2, cada término an está definido por la relación de recurrencia an = 2an − 1.
Definición 7.1.1. Sucesión infinita
|
Una sucesión infinita {an} es una lista ordenada de números de la forma a1, a2, a3, … , an, … El subíndice n se denomina índice variable de la sucesión. Cada número an es un término de la sucesión. A veces, las sucesiones se definen mediante fórmulas explícitas, en cuyo caso an = f (n) para alguna función f (n) definida sobre los enteros positivos. En otros casos, las sucesiones se definen mediante el uso de una relación de recurrencia. En una relación de recurrencia, un término (o más) de la secuencia se da explícitamente, y los términos posteriores se definen a partir de términos anteriores de la sucesión |
Tenga en cuenta que el índice no tiene que comenzar en n = 1, podría comenzar con otro entero. Por ejemplo, una sucesión dada por la fórmula explícita an = f (n) podría comenzar en n = 0, en cuyo caso la secuencia sería a0, a1, a2, …
De manera similar, para una secuencia definida por una relación de recurrencia, el término a₀ puede darse explícitamente, y los términos an para n ≥ 1 pueden definirse en términos de an − 1. Como una secuencia {an} tiene exactamente un valor para cada entero positivo n, puede describirse como una función cuyo dominio es el conjunto de enteros positivos. Como resultado, tiene sentido discutir acerca de la gráfica de una sucesión. La gráfica de una secuencia {an} consiste en los puntos (n, an) para todos los enteros positivos n. La figura 7.1_1 muestra la gráfica de {2n}.

(Figura 7.1_1 Los puntos trazados representan una gráfica de la sucesión {2ⁿ}.)
Sucesiones aritméticas y geométricas
Dos tipos de sucesiones ocurren con frecuencia y reciben nombres especiales: sucesiones aritméticas y sucesiones geométricas.
♣ En una sucesión aritmética, la diferencia entre cada par de términos consecutivos es la misma. Por ejemplo, considere la sucesión
3, 7, 11, 15, 19,….
Puede ver que la diferencia entre cada par de términos consecutivos es 4. Suponiendo que este patrón continúe, se trata de una sucesión aritmética. Se puede describir esta sucesión utilizando la relación de recurrencia

Tenga en cuenta que

Por lo tanto, el enésimo término de la secuencia también se puede describir utilizando la fórmula explícita
![]()
En general, una sucesión aritmética es cualquier secuencia con término enésimo de la forma
donde:
- es el primer término de la sucesión,
- d es la diferencia común entre los términos consecutivos,
- es la posición del término en la sucesión.
♣ En una sucesión geométrica, la razón de cada par de términos consecutivos es la misma. Por ejemplo, considere la secuencia
![]()
Vemos que la razón de cualquier término al término precedente es −1/3. Suponiendo que este patrón continúa, esta secuencia es una sucesión geométrica. Se puede definir recursivamente como

Alternativamente, dado que

la secuencia se puede describir usando la fórmula explícita

La secuencia {2n} que discutimos anteriormente es una sucesión geométrica, donde la razón de cualquier término al término anterior es 2.
En general, una sucesión geométrica es cualquier secuencia cuyo término enésimo tiene la forma
![]()
Donde c es el primer término de la sucesión y r es razón de cada par de términos consecutivos.
EJEMPLO ILUSTRATIVO 7.1_1. Encontrar fórmulas explícitas para dos sucesiones
Para cada una de las siguientes sucesiones, encuentre una fórmula explícita para el enésimo término.

Solución:
a. Primero, tenga en cuenta que los términos de la sucesión se alternan de negativos a positivos. Los términos impares en la secuencia son negativos y los términos pares son positivos. Por lo tanto, el enésimo término incluye el factor (−1)n. Luego, considere la secuencia de numeradores {1, 2, 3, …} y la secuencia de denominadores {2, 3, 4, …}. Podemos ver que ambas secuencias son secuencias aritméticas. El enésimo término en la secuencia de numeradores es n, y el enésimo término en la secuencia de denominadores es n + 1. Por lo tanto, la sucesión se puede describir mediante la fórmula explícita

b. La sucesión de numeradores 3, 9, 27, 81, 243, … es una secuencia geométrica. El numerador del enésimo término es 3n. La secuencia de denominadores 4, 7, 10, 13, 16, … es una secuencia aritmética. El denominador del enésimo término es 4 + 3 (n − 1) = 3n + 1. Por lo tanto, podemos describir la sucesión mediante la fórmula explícita

Ejercicio de control 7.1_1
Encuentre una fórmula explícita para el enésimo término de la secuencia {1/5, −1/7, 1/9, −1/11, …}. ♦
EJEMPLO ILUSTRATIVO 7.1_2. Sucesión definida por relaciones de recurrencia
Para cada una de las siguientes secuencias definidas recursivamente, encuentre una fórmula explícita para la sucesión.
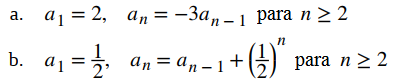
Solución:
a. Escribiendo los primeros términos, tenemos

En general,![]() b. Escribimos los primeros términos:
b. Escribimos los primeros términos:

De este patrón, deducimos la fórmula explícita

Ejercicio de control 7.1_2
Encuentre una fórmula explícita para la secuencia definida recursivamente tal que a1 = −4 y an = an − 1 + 6. ♦
Límite de una sucesión
Una pregunta fundamental que surge con respecto a las secuencias infinitas es el comportamiento de los términos a medida que n aumenta. Dado que una secuencia es una función definida en los enteros positivos, tiene sentido discutir el límite de los términos cuando n → ∞. Por ejemplo, considere las siguientes cuatro secuencias y sus diferentes comportamientos cuando n → ∞ (consulte la Figura 7.1_2):
a. {1 + 3n} = {4, 7, 10, 13, …}. Los términos 1 + 3n se vuelven arbitrariamente grandes cuando n → ∞. En este caso, decimos que 1 + 3n → ∞ cuando n → ∞.
b. {1− (1/2)n} = {1/2, 3/4, 7/8, 15/16, …}. Los términos 1 − (1/2)n → 1 cuando n → ∞.
c. {(−1)n} = {−1, 1, −1, 1 , …}. Los términos se alternan pero no se acercan a un solo valor cuando n → ∞.
d. {(−1)n/n} = {−1, 1/2, −1/3, 1/4, …}. Los términos también se alternan para esta secuencia, pero (−1)n/n → 0 cuando n → ∞.
 |  |
 |  |
A partir de estos ejemplos, vemos varias posibilidades para el comportamiento de los términos de una secuencia cuando n → ∞. En dos de las sucesiones, los términos se acercan a un número finito cuando n → ∞. En las otras dos secuencias, los términos no se acercan a un número finito cuando n → ∞. Si los términos de una secuencia se acercan a un número finito L cuando n → ∞, decimos que la secuencia es una secuencia convergente y el número real L es el límite de la secuencia. Podemos dar una definición informal aquí.
Definición 7.1.2. Límite de una sucesión (definición informal)
|
Dada una secuencia {an}, si los términos an se acercan arbitrariamente a un número finito L cuando n se vuelve lo suficientemente grande, decimos que {an} es una sucesión convergente y L es el límite de la sucesión. En este caso, escribimos limn → ∞ an = L. Si una secuencia {an} no es convergente, decimos que es una secuencia divergente. |
En la figura 7.1_2 (b), vemos que los términos de la secuencia {1− (1/2)n} se acercan arbitrariamente a 1 a medida que n se vuelve muy grande. Concluimos que {1− (1/2)n} es una secuencia convergente y su límite es 1. En contraste, en la Figura 7.1_2 (a), vemos que los términos en la secuencia 1 + 3n no se acercan a un número finito cuando n se hace más grande. Decimos que {1 + 3n} es una secuencia divergente.
En la definición informal del límite de una secuencia, usamos los términos “arbitrariamente cerca” y “suficientemente grande”. Aunque estas frases ayudan a ilustrar el significado de una secuencia convergente, son algo vagas. Para ser más precisos, ahora presentamos la definición formal de límite para una secuencia e ilustramos estas ideas gráficamente en la Figura 7.1_3.
Definición 7.1.3. Límite de una sucesión (definición formal)
|
Una secuencia {an} converge a un número real L si para todo ε > 0, existe un entero N tal que | an − L | < ε si n ≥ N. El número L es el límite de la secuencia y escribimos limn → ∞ an = L o an → L. En este caso, decimos que la secuencia {an} es una secuencia convergente. Si una secuencia no converge, es una secuencia divergente y decimos que el límite no existe. |
Observamos que la convergencia o divergencia de una secuencia {an} depende solo de lo que sucede con los términos an cuando n → ∞. Por lo tanto, si un número finito de términos b1, b2,…, bN se colocan antes de a1 para crear una nueva secuencia
b1, b2,…, bN, a1, a2,…,
esta nueva secuencia convergerá si {an} converge y divergirá si {an} diverge. Además, si la secuencia {an} converge a L, esta nueva secuencia también convergerá a L.

Como se definió anteriormente, si una secuencia no converge, se dice que es una secuencia divergente. Por ejemplo, las secuencias {1 + 3n} y {(−1)n} que se muestran en la Figura 7.1_2 divergen. Sin embargo, diferentes secuencias pueden divergir de maneras distintas. La secuencia {(−1)n} diverge porque los términos alternan entre 1 y −1, pero no se acercan a un valor cuando n → ∞. Por otro lado, la secuencia {1 + 3n} diverge porque los términos 1 + 3n → ∞ cuando n → ∞. Decimos que la secuencia {1 + 3n} diverge hasta el infinito y escribimos limn → ∞ (1 + 3n) = ∞. Es importante reconocer que esta notación no implica que exista el límite de la secuencia {1 + 3n}. De hecho, la secuencia es divergente. Escribir que el límite es infinito solo tiene la intención de proporcionar más información sobre por qué la secuencia es divergente. Una secuencia también puede divergir hasta el infinito negativo. Por ejemplo, la secuencia {−5n + 2} diverge al infinito negativo porque −5n + 2 → −∞ cuando n → ∞. Escribimos esto como limn → ∞ (−5n + 2) = −∞.
Debido a que una secuencia es una función cuyo dominio es el conjunto de números enteros positivos, podemos usar las propiedades de los límites de funciones para determinar si una secuencia converge. Por ejemplo, considere una secuencia {an} y una función relacionada f definida en todos los números reales positivos tal que f (n) = an para todos los enteros n ≥ 1. Dado que el dominio de la secuencia es un subconjunto del dominio de f, si limx → ∞ f (x) existe, entonces la secuencia converge y tiene el mismo límite. Por ejemplo, considere la secuencia {1/n} y la función relacionada f (x) = 1/x. Dado que la función f definida en todos los números reales x > 0 satisface f (x) = 1/x → 0 cuando x → ∞, la secuencia {1/n} debe satisfacer 1/n → 0 cuando n → ∞.
TEOREMA 7.1.1 Límite de una secuencia definida por una función
Considere una secuencia {an} tal que an = f (n) para todo n ≥ 1. Si existe un número real L tal que
limx → ∞ f (x) = L,
entonces {an} converge y
limn → ∞ an = L. ♦
Podemos usar este teorema y evaluar el limn → ∞ r n para 0 ≤ r ≤ 1. Por ejemplo, considere la secuencia {(1/2)n} y la función exponencial relacionada f (x) = (1/2)x. Como limx → ∞ (1/2)x = 0, concluimos que la secuencia {(1/2)n} converge y su límite es 0. De manera similar, para cualquier número real r tal que 0 ≤ r < 1, limx → ∞ r x = 0, y por lo tanto la secuencia {r n} converge a 0. Por otro lado, si r = 1, entonces limx → ∞ r x = 1, y por ende el límite de la secuencia {1n} es 1. Si r > 1, limx → ∞ r x = ∞, y por lo tanto no podemos aplicar el teorema. Sin embargo, en este caso, al igual que la función r x crece sin límite cuando n → ∞, los términos r n en la secuencia se vuelven arbitrariamente grandes cuando n → ∞, y concluimos que la secuencia {r n} diverge hasta el infinito si r > 1.
Resumimos estos resultados con respecto a la secuencia geométrica {r n}:
r n → 0 si 0 < r < 1
r n → 1 si r = 1
r n → ∞ si r > 1.
Más adelante en esta sección analizamos el caso cuando r < 0.
Ahora consideramos secuencias un poco más complicadas. Por ejemplo, considere la secuencia {(2/3)n + (1/4)n}. Los términos en esta secuencia son más complicados que otras secuencias que hemos discutido, pero afortunadamente el límite de esta secuencia está determinado por los límites de las dos secuencias (2/3)n y (1/4)n. Como describimos en las siguientes leyes de límites algebraicos, dado que (2/3)n y (1/4)n ambos convergen a 0, la secuencia {(2/3)n + (1/4)n} converge a 0 + 0 = 0. Así como pudimos evaluar un límite que involucra una combinación algebraica de funciones f y g al observar los límites de f y g (ver Introducción a los límites), podemos evaluar el límite de una secuencia cuyos términos son combinaciones algebraicas de an y bn evaluando los límites de {an} y {bn}.
TEOREMA 7.1.2 Leyes de límites algebraicos
|
Dadas las secuencias {an} y {bn} y cualquier número real c, si existen constantes A y B tales que limn →∞ an = A y limn → ∞ bn = B, entonces
|
Prueba
Probamos la parte iii.
Sea ϵ > 0. Como limn→ ∞ an = A, existe un entero positivo constante N1 tal que ∣an − A∣ < ε / 2 para todos los n ≥ N1.
Como limn→∞ bn = B, existe una constante N2 tal que | bn − B | < ε / 2 para todos los n ≥ N2. Sea N el mayor de N1 y N2.
Por lo tanto, para todos los n ≥ N, | (an + bn) − (A + B) | ≤ | an − A | + | bn − B | < ε / 2 + ε / 2 = ε.
Las leyes algebraicas de límites nos permiten evaluar los límites de muchas sucesiones. Por ejemplo, considere la secuencia {1/n²}. Como se mostró anteriormente, limn→∞ 1/n = 0. Del mismo modo, para cualquier entero positivo k, podemos concluir que En el siguiente ejemplo, hacemos uso de este hecho junto con las leyes de límites para evaluar los límites de otras secuencias.
En el siguiente ejemplo, hacemos uso de este hecho junto con las leyes de límites para evaluar los límites de otras secuencias.
EJEMPLO ILUSTRATIVO 7.1_3. Determinación de la convergencia y búsqueda de límites
Para cada una de las siguientes sucesiones, determine si la secuencia converge o no. Si converge, encuentre su límite.


Solución:
a. Sabemos que 1/n → 0. Usando este hecho, concluimos que
![]()
Por lo tanto,

La secuencia converge y su límite es 5.
b. Al factorizar n4 fuera del numerador y el denominador y usar las leyes de límites anteriores, tenemos

La secuencia converge y su límite es −3/4.
c. Considere la función relacionada f (x) = 2x/x² definida en todos los números reales x > 0. Dado que 2x → ∞ y x² → ∞ cuando x → ∞, aplique la regla de L’Hôpital dos veces seguidas (derivando tanto el numerador como el denominador cada vez) y escriba

Concluimos que la secuencia diverge a más infinito.
d. Considere la función f (x) = (1 + 4/x)x definida en todos los números reales x > 0. Esta función tiene la forma indeterminada 1∞ cuando x → ∞. Sea

Ahora tomando el logaritmo natural de ambos lados de la ecuación, obtenemos

Como la función f (x) = lnx es continua en su dominio, podemos intercambiar el límite y el logaritmo natural. Por lo tanto,

Usando propiedades de logaritmos, escribimos

Como el lado derecho de esta ecuación tiene la forma indeterminada ∞⋅0, escríbala como una fracción para aplicar la regla de L’Hôpital. Se tiene
![]()
Como el lado derecho ahora está en forma indeterminada 0/0, podemos aplicar la regla de L’Hôpital. Concluimos que

Por lo tanto, ln(y) = 4 e y = e⁴. Por lo tanto, dado que limx → ∞ (1 + 4/x)x = e⁴, podemos concluir que la secuencia {(1 + 4/n)n} converge a e⁴. ♦
Ejercicio de control 7.1_3
Recuerde que si f es una función continua en un valor L, entonces f (x) → f (L) cuando x → L. Esta idea también se aplica a las sucesiones. Suponga que una sucesión an → L, y que f es una función de valores reales continua en L, entonces f (an) → f (L). Esta propiedad a menudo nos permite encontrar límites para sucesiones complicadas.
Por ejemplo, considere la sucesión con fórmula para el término enésimo

Como la sucesión 5 − 3/n² → 5 cuando n → ∞ y como √x es una función continua en x = 5, entonces

Teorema 7.1.3. Funciones continuas definidas en sucesiones convergentes
Considere una sucesión {an} y suponga que existe un número real L tal que la sucesión {an} converge a L. Suponga además que f es una función continua en L. Entonces existe un número entero N tal que f está definida en todos los valores an para n ≥ N, y la sucesión {f (an)} converge a f (L) (Figura 7.1_4).

(Figura 7.1_4 Debido a que f es una función continua y dado que las entradas a1, a2, a3, … se acercan a L, las salidas f (a1), f (a2), f (a3), … se acercan a f (L).) ♦
Prueba
Sea ϵ > 0. Dado que f es continua en L, existe δ > 0 tal que | f (x) − f (L) | < ε si |x − L| < δ. Dado que la sucesión {an} converge a L, existe un N tal que |an − L| < δ para todos los n ≥ N. Por lo tanto, para todos los n ≥ N, |an − L| < δ, lo que implica | f (an) − f (L) | < ε. Concluimos que la secuencia {f (an)} converge en f (L).
EJEMPLO ILUSTRATIVO 7.1_4. Límites que implican funciones continuas definidas en secuencias convergentes
Determine si la secuencia {cos (3/n²)} converge. Si converge, encuentre su límite.
Solución:
Como la secuencia {3/n²} converge a 0 y cosx es continua en x = 0, podemos concluir que la secuencia {cos (3/n²)} converge y

Ejercicio de control 7.1_4
Otro teorema que involucra límites de sucesiones es una extensión del Teorema de compresión para límites discutido en Introducción a los límites.
Teorema 7.1.4. Teorema de compresión para secuencias
|
Considere las secuencias {an}, {bn} y {cn}. Suponga que existe un entero N tal que an ≤ bn ≤ cn para todos los n ≥ N. Si existe un número real L tal que limn → ∞ an = L = limn → ∞ cn, entonces {bn} converge y limn → ∞ bn = L (Figura 7.1_5).
Figura 7.1_5 Cada término bn satisface an ≤ bn ≤ cn y las secuencias {an} y {cn} convergen al mismo límite, por lo que la secuencia {bn} debe converger también a este mismo límite. ♦ |
Prueba
Sea ε > 0. Dado que la secuencia {an} converge a L, existe un número entero N1 tal que | an − L | < ε para todos los n ≥ N1. De manera similar, dado que {cn} converge a L, existe un número entero N2 tal que | cn − L | < ε para todos los n ≥ N2. Por supuesto, existe un número entero N tal que an ≤ bn ≤ cn para todos los n ≥ N. Sea M el mayor de N1, N2 y N. Debemos demostrar que | bn − L | < ε para todos los n ≥ M.
Para todos los n ≥ M,
EJEMPLO ILUSTRATIVO 7.1_5. Usando el teorema de compresión
Usa el teorema de compresión para encontrar el límite de cada una de las siguientes secuencias.
a. {cosn/n2}
b. {(−1/2)n}
Solución:
a. Dado que −1 ≤ cosn ≤ 1 para todos los enteros n, tenemos

Como −1/n2 → 0 y 1/n2 → 0, concluimos que cosn/n2 → 0 también.
b. Debido a que

para todos los enteros positivos n, −1/2n → 0 y 1/2n → 0, podemos concluir que (−1/2)n → 0.
Ejercicio de control 7.1_5
Encuentre limn → ∞ (2n − senn)/n. ♦
Usando la idea del ejemplo 7.1_5 b. concluimos que r n → 0 para cualquier número real r tal que −1 < r < 0. Si r < −1, la secuencia {r n} diverge porque los términos oscilan y se vuelven arbitrariamente grandes en magnitud. Si r = −1, la secuencia {r n} = {(−1)n} diverge, como se discutió anteriormente. A continuación se muestra un resumen de las propiedades de las secuencias geométricas.
r n → 0 si | r | < 1
r n → 1 si r = 1
r n → ∞ si r > 1
{r n} diverge si r ≤ − 1
Sucesiones acotadas
Ahora dirigimos nuestra atención a uno de los teoremas más importantes que involucran sucesiones: el Teorema de la convergencia monótona. Antes de establecer el teorema, necesitamos introducir algo de terminología y motivación. Comenzamos definiendo lo que significa que una sucesión esté acotada.
Definición 7.1.4. Sucesión acotada
|
Una sucesión {an} se dice que está acotada por arriba si existe un número real M tal que an ≤ M para todos los enteros positivos n. Una sucesión {an} se dice que está acotada por abajo si existe un número real M tal que M ≤ an para todos los enteros positivos n. Una sucesión {an} es una sucesión acotada si está acotada por arriba y acotada por abajo. Si una secuencia no está acotada, se dice que es una sucesión no acotada. |
Por ejemplo, la sucesión {1/n} está acotada superiormente porque 1/n ≤ 1 para todos los enteros positivos n. También se dice que está acotada inferiormente porque 1/n ≥ 0 para todos los enteros positivos n. Por lo tanto, {1 /n} es una sucesión acotada.
Por otro lado, considere la secuencia {2n}. Debido a que 2n ≥ 2 para todos los n ≥ 1, la sucesión está acotada inferiormente. Sin embargo, la sucesión no está acotada superiormente. Por lo tanto, {2n} es una sucesión no acotada.
Ahora discutimos la relación entre la acotación y la convergencia. Supongamos que una sucesión {an} no está acotada. Entonces no está acotada por arriba, o no está acotada por abajo, o ambos. En cualquier caso, hay términos an que son arbitrariamente grandes en magnitud (o en valor absoluto) a medida que n se hace más grande. Como resultado, la sucesión {an} no puede converger. Por lo tanto, estar acotada es una condición necesaria para que una sucesión converja.
Teorema 7.1.5. Las sucesiones convergentes están acotadas
Si una secuencia {an} converge, entonces está acotada. ♦
Tenga en cuenta que ser acotada no es una condición suficiente para que una sucesión converja.
Por ejemplo, la sucesión {(−1) n} está acotada, pero diverge porque oscila entre 1 y −1 y nunca se acerca a un número finito. Ahora discutimos una condición suficiente (pero no necesaria) para que una sucesión acotada converja.
Considere una sucesión acotada {an}. Supongamos que la sucesión {an} está creciendo. Es decir, a1 ≤ a2 ≤ a3 . . . Como la sucesión está aumentando, los términos no son oscilantes. Por lo tanto, hay dos posibilidades. La sucesión podría divergir hasta el infinito, o podría converger. Sin embargo, dado que la sucesión está acotada, está acotada superiormente y la sucesión no puede divergir hasta el infinito. Concluimos que {an} converge. Por ejemplo, considere la sucesión
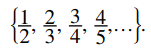
Dado que esta sucesión está creciendo y está acotada superiormente, converge. Ahora, considere la sucesión
![]()
Aunque la sucesión no está creciendo para todos los valores de n, vemos que −1/2 < −1/3 < −1/4 < … . Por lo tanto, comenzando con el octavo término, a8 = −1/2, la sucesión está creciendo. En este caso, decimos que la sucesión eventualmente crece. Como la sucesión está acotada superiormente, converge. También es cierto que si una sucesión está decreciendo (o eventualmente decrece) y acotada a continuación, también converge.
Definición 7.1.5. Sucesiones crecientes y decrecientes
|
Una secuencia {an} es creciente para todo n ≥ n0 si an ≤ an + 1 para todo n ≥ n0. Una secuencia {an} es decreciente para todo n ≥ n0 si an ≥ an + 1 para todo n ≥ n0. Una secuencia {an} es una secuencia monótona para todos los n ≥ n0 si crece para todos los n ≥ n0 o decrece para todos los n ≥ n0. |
Ahora tenemos las definiciones necesarias para enunciar el Teorema de convergencia monótona, que da una condición suficiente para la convergencia de una secuencia.
Teorema 7.1.6. Teorema de convergencia monótona
| Si {an} es una secuencia acotada y existe un entero positivo n0 tal que {an} es monótona para todos los n ≥ n0, entonces {an} converge. |
La demostración de este teorema está más allá del alcance de este texto. En cambio, proporcionamos un gráfico para mostrar intuitivamente por qué este teorema tiene sentido (figura 7.1_6).

En el siguiente ejemplo, mostramos cómo se puede utilizar el Teorema de convergencia monótona para demostrar la convergencia de una secuencia.
EJEMPLO ILUSTRATIVO 7.1_6. Uso del teorema de convergencia monótona
Para cada una de las siguientes secuencias, use el Teorema de convergencia monótona para mostrar que la secuencia converge y encuentre su límite.
a. {4n/n!}
b. {an} definido de forma recursiva de modo que
a1 = 2 y an + 1 = an/2 + 1/2an para todo n ≥ 2.
Solución:
a. Al escribir los primeros términos, vemos que

Al principio, los términos crecen. Sin embargo, después del tercer término, los términos decrecen. De hecho, los términos decrecen para todos los n ≥ 3. Podemos mostrar esto de la siguiente manera.

Por lo tanto, la secuencia es decreciente para todos los n ≥ 3. Además, la secuencia está acotada por abajo por 0 porque 4n/n! ≥ 0 para todos los enteros positivos n. Por lo tanto, según el Teorema de convergencia monótona, la secuencia converge.
Para encontrar el límite, usamos el hecho de que la secuencia converge y sea L = limn → ∞ an. Ahora considere la siguiente observación. Examine limn → ∞ an + 1. Teniendo presente que

la única diferencia entre las secuencias {an + 1} y {an} es que {an + 1} omite el primer término. Dado que un número finito de términos no afecta la convergencia de una secuencia,

Combinando este hecho con la ecuación

y tomando el límite de ambos lados de la ecuación

podemos concluir que
L = 0⋅L = 0.
b. Escribiendo los primeros términos,
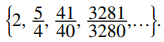
podemos conjeturar que la sucesión es decreciente y está limitada por debajo por 1. Para establecer que la sucesión está acotada inferiormente por 1, basta demostrar que

Primero, se reescribe

Dado que a1 > 0 y a2 se define como una suma de términos positivos, a2 > 0. De manera similar, todos los términos an > 0. Por lo tanto,
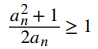
si y solo si
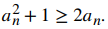
Reescribiendo la desigualdad an2 + 1 ≥ 2an como an2 − 2an + 1 ≥ 0, y usando el hecho de que
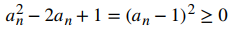
debido a que el cuadrado de cualquier número real es no negativo, podemos concluir que
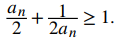
Para establecer que la secuencia es decreciente, debemos probar que an+1 ≤ an para todo n ≥ 1. Dado que 1 ≤ an2, se deduce que
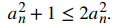
Dividiendo ambos lados por 2an, obtenemos

Usando la definición de an + 1, llegamos a la conclusión de que

Dado que {an} está acotada por abajo y es decreciente, según el Teorema de convergencia monótona, converge.
Para encontrar el límite, sea L = limn → ∞ an. Luego, usando la relación de recurrencia y el hecho de que limn → ∞ an = limn → ∞ an + 1, tenemos
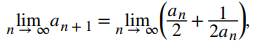
y por lo tanto

Multiplicando ambos lados de esta ecuación por 2L, llegamos a la ecuación

Resolviendo esta ecuación para L, llegamos a la conclusión de que L2 = 1, lo que implica L = ± 1. Dado que todos los términos son
positivo, el límite es L = 1. ♦
Ejercicio de control 7.1_6
Considere la secuencia {an} definida recursivamente tal que a1 = 1, an = an − 1/2. Utilice el Teorema de convergencia monótona para demostrar que esta secuencia converge y encuentre su límite. ♦


Gracias por compartir sus conocimientos sobre este tema clave. Saludos mi profe |