| 7. Sucesiones y series infinitas | 7.2 Series infinitas |

Ejercicios propuestos para el Capítulo 7.2

       Usando la notación sigma, escribe las siguientes expresiones como series infinitas.

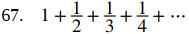
68. 1 − 1 + 1 − 1 + ⋯

70. sen1 + sen1/2 + sen1/3 + sen1/4 + ⋯

       Calcule las primeras cuatro sumas parciales S₁,…, S₄ para la serie que tiene un término a_n y comienza con n = 1 de la siguiente manera.

71.  a_n = n
72.  a_n = 1/n
73.  a_n = sen(nπ/2)
74.  a_n = (−1)ⁿ

       En los siguientes ejercicios, calcule el término general a_n de la serie con la suma parcial S_n dada. Si la secuencia de sumas parciales converge, encuentre su límite S.

75.  S_n = 1 − 1/n, n ≥ 2
76.  S_n = n(n + 1)/2, n ≥ 1
77.  S_n = √n, n ≥ 2
78.  S_n = 2 − (n + 2)/2ⁿ, n ≥ 1

       Para cada una de las siguientes series, use la secuencia de sumas parciales para determinar si la serie converge o diverge.

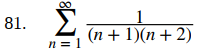  Sugerencia: use una descomposición de fracciones parciales como esa para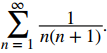

  Sugerencia: siga el razonamiento para

       Suponga qu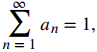e que que a₁ = 2 y b₁ = −3. Encuentra la suma de la serie indicada.

       Indique si la serie dada converge y explique por qué.

  Sugerencia: vuelva a escribir usando un cambio de índice.

  Sugerencia: Reescriba la serie usando un cambio de índice.

      Para a_n de la siguiente manera, escriba la suma como una serie geométrica de la forma  Indique si la serie converge y, si lo hace, encuentre el valor de ∑a_n.

93.  a₁ = −1  y  a_n/a_{n + 1} = −5  para  n ≥ 1.
94.  a₁ = 2  y  a_n/a_{n + 1} = 1/2  para  n ≥ 1.
95.  a₁ = 10  y  a_n/a_{n + 1} = 10  para  n ≥ 1.
96.  a₁ = 1/10  y  a_n/a_{n + 1} = −10  para  n ≥ 1.

       Usa la identidad para expresar la función como una serie geométrica en el término indicado.

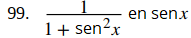
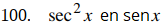
       Evalúe la siguiente serie telescópica o indique si la serie diverge.

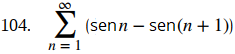
      Exprese la siguiente serie como una suma telescópica y evalúe su enésima suma parcial.

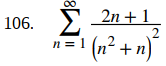  (Sugerencia: factoriza el denominador y usa fracciones parciales).

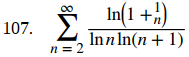
  (Sugerencia: mire 1/(n2ⁿ).)

      Una serie telescópica general es aquella en la que todos los términos, excepto los primeros, se cancelan después de sumar un número determinado de términos sucesivos.

109.  Sea a_n = f (n) − 2 f (n + 1) + f (n + 2), en la cual f (n) → 0 cuando n → ∞. Encontrar

110.  Sea a_n = f (n) −  f (n + 1) −  f (n + 2) + f (n + 3), en la cual f (n) → 0 cuando n → ∞. Encontrar

111. Suponga que a_n = c₀ f (n) + c₁ f (n + 1) + c₂ f (n + 2) + c₃ f (n + 3) + c₄ f (n + 4), donde f (n) → 0 cuando n → ∞. Encuentre una condición en los coeficientes c₀,…, c₄ que hagan de esta una serie telescópica general.

112.  Evalúe 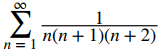.   Sugerencia: .

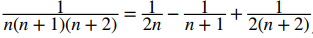113.  Evaluar

114.  Encuentra una fórmula para donde N es un número entero positivo.

Proyecto estudiantil. Constante de Euler.

Hemos demostrado que la serie armónica \[ \sum_{n=1}^{\infty}\frac{1}{\mathit{n}} \] diverge. Aquí investigamos el comportamiento de las sumas parciales \( S_{\mathit{k}} \) cuando \( \mathit{k} \rightarrow \infty \). En particular, indicamos que se comportan como la función logaritmo natural mostrando que existe una constante \( \gamma \) tal que \[ \sum_{n=1}^{\mathit{k}}\frac{1}{\mathit{n}}~-~\ln\mathit{k} ~ \rightarrow \gamma ~ \quad \text{cuando} \quad \mathit{k} \rightarrow \infty. \] Esta constante \( \gamma \) se conoce como la constante de Euler.

1. Sea \[ T_{\mathit{k}} = \sum_{n=1}^{\mathit{k}}\frac{1}{\mathit{n}}~-~\ln\mathit{k}. \] Evalúe \( T_{\mathit{k}} \) para varios valores de \( \mathit{k} \).

2. Para \( T_{\mathit{k}} \) como se define en la parte 1, muestre que la secuencia \( \{T_{\mathit{k}}\} \) converge usando los siguientes pasos.

3. Ahora estime qué tan lejos está \( T_{\mathit{k}} \) de \( \gamma \) para un entero \( \mathit{k} \) dado. Demuestre que para \( \mathit{k} \geq 1, \, 0 < T_{\mathit{k}}~-~\gamma \leq \frac{1}{\mathit{k}} \) usando los siguientes pasos.