| 4.7 Problemas de optimización |
Ejercicios propuestos para el Capítulo 4.7
Para los siguientes ejercicios, responda por demostración, contraejemplo o explicación:
-
Cuando encuentra el máximo para un problema de optimización, ¿por qué necesita verificar el signo de la derivada alrededor de los puntos críticos?
-
¿Por qué necesita verificar los puntos extremos para los problemas de optimización?
-
Verdadero o Falso. Para cada función no lineal continua, puede encontrar el valor x que maximiza la función.
-
Verdadero o Falso. Para cada función no constante continua en un dominio cerrado y finito, existe al menos un x que minimiza o maximiza la función.
Para los siguientes ejercicios, plantee y evalúe cada problema de optimización:
315. Para llevar una maleta en un avión, la longitud + ancho + alto de la caja debe ser menor o igual a 62 pulgadas. Asumiendo que la base de la maleta es cuadrada, muestre que el volumen es \(V = h(31 – \frac{1}{2}h)^2\). ¿Qué altura permite tener el mayor volumen?
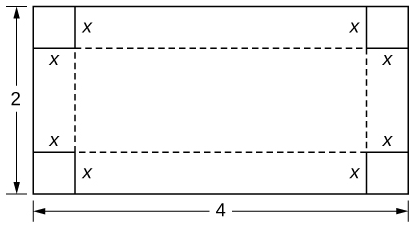
316. Estás construyendo una caja de cartón con las dimensiones de 2 m por 4 m. Luego cortas cuadrados del mismo tamaño en cada esquina para poder doblar los bordes. ¿Cuáles son las dimensiones de la caja con el mayor volumen?
317. Encuentra el entero positivo que minimiza la suma del número y su recíproco.
318. Encuentra dos enteros positivos tales que su suma sea 10, y minimiza y maximiza la suma de sus cuadrados.
Para los siguientes ejercicios, considere la construcción de un corral para encerrar un área:
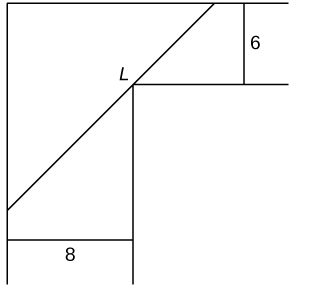
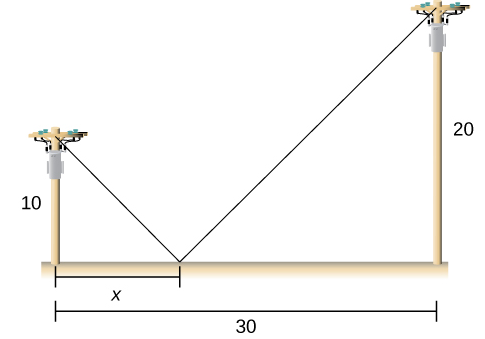
- [T] Te estás mudando a un nuevo apartamento y notas que hay una esquina donde el pasillo se estrecha de 8 pies a 6 pies. ¿Cuál es la longitud del objeto más largo que se puede transportar horizontalmente alrededor de la esquina?
324. El pulso de un paciente mide 70 lpm, 80 lpm y luego 120 lpm. Para determinar una medición precisa del pulso, el médico quiere saber qué valor minimiza la expresión \[(x-70)^2 + (x-80)^2 + (x-120)^2.\] ¿Qué valor lo minimiza?
325. En el problema anterior, asuma que el paciente estaba nervioso durante la tercera medición, por lo que solo ponderamos ese valor la mitad que los demás. ¿Cuál es el valor que minimiza \[(x-70)^2 + (x-80)^2 + \frac{1}{2}(x-120)^2?\]
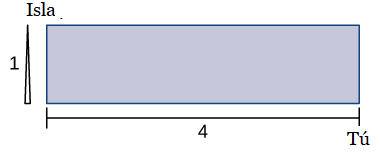
- Puedes correr a una velocidad de 6 mph y nadar a una velocidad de 3 mph. Te encuentras en la orilla, a 4 millas al este de una isla que está a 1 milla al norte de la costa. ¿Cuánto debes correr hacia el oeste para minimizar el tiempo necesario para llegar a la isla?
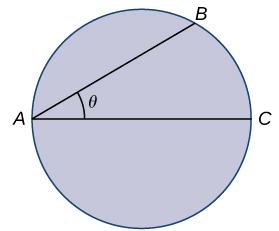
Para los siguientes problemas, considere a un salvavidas en una piscina circular con un diámetro de 40 m. Debe llegar a alguien que se está ahogando en el lado opuesto de la piscina, en la posición C. El salvavidas nada con una velocidad v y corre alrededor de la piscina a una velocidad w = 3v:
-
Encuentra una función que mida el tiempo total que toma llegar a la persona que se está ahogando en función del ángulo de nado θ.
-
Encuentra el ángulo θ al que el salvavidas debe nadar para llegar a la persona que se está ahogando en el menor tiempo posible.
- Un camión consume gasolina según la función g(v) = av + b/v, donde v representa la velocidad del camión y g representa los galones de combustible por milla. Suponiendo que a y b son positivos, ¿a qué velocidad se minimiza el consumo de combustible?
Para los siguientes ejercicios, considere una limusina que obtiene \( m(v) = \frac{120 – 2v}{5} \, \text{mi/gal} \) a una velocidad \( v \), el chófer cuesta \( 15 \, \text{\$}/\text{h} \), y la gasolina cuesta \( 3.5 \, \text{\$}/\text{gal}: \)
-
Encuentra el costo por milla a la velocidad v.
-
Encuentra la velocidad de conducción más económica.
Para los siguientes ejercicios, considere una pizzería que vende pizzas por un ingreso de R(x) = ax y costos de C(x) = b + cx + dx², donde x representa el número de pizzas; a > c:
332. Encuentre la función de ganancia para el número de pizzas. ¿Cuántas pizzas dan la mayor ganancia por pizza?
333. Asuma que \(R(x)=10x\) y \(C(x)=2x+x^{2}\). ¿Cuántas pizzas vendidas maximizan la ganancia?
334. Asuma que \(R(x)=15x\), y \(C(x)=60+3x+\frac{1}{2}x^{2}\). ¿Cuántas pizzas vendidas maximizan la ganancia?
Para los siguientes ejercicios, considere un alambre de 4 pies de largo cortado en dos pedazos. Un pedazo forma un círculo con radio r y el otro forma un cuadrado de lado x:
-
Elija x para maximizar la suma de sus áreas.
-
Elija x para minimizar la suma de sus áreas.
Para los siguientes ejercicios, considere dos números no negativos x e y tales que x + y = 10. Maximice y minimice las cantidades:
337. \(xy\)
338. \(x^{2}y^{2}\)
339. \(y-\frac{1}{x}\)
340. \(x^{2}-y\)
Para los siguientes ejercicios, dibuje el problema de optimización dado y resuelva:
-
Encuentra el volumen del cilindro circular recto más grande que cabe en una esfera de radio 1.
-
Encuentra el volumen del cono recto más grande que cabe en una esfera de radio 1.
-
Encuentra el área del rectángulo más grande que cabe en el triángulo con lados x = 0, y = 0 y x/4 + y/6 = 1.
-
Encuentra el mayor volumen de un cilindro que cabe dentro de un cono que tiene un radio de base R y altura h.
-
Encuentra las dimensiones del cilindro cerrado con volumen V = 16π que tiene la menor cantidad de área de superficie.
-
Encuentra las dimensiones de un cono recto con área de superficie S = 4π que tiene el mayor volumen.
Para los siguientes ejercicios, considere los puntos en las gráficas dadas. Utilice una calculadora para graficar las funciones:
-
[T] ¿Dónde está la línea y = 5 − 2x más cerca del origen?
-
[T] ¿Dónde está la línea y = 5 − 2x más cerca del punto (1, 1)?
-
[T] ¿Dónde está la parábola y = x² más cerca del punto (2, 0)?
-
[T] ¿Dónde está la parábola y = x² más cerca del punto (0, 3)?
Para los siguientes ejercicios, plantee, pero no evalúe, cada problema de optimización:
- Una ventana está compuesta por un semicírculo colocado encima de un rectángulo. Si tiene 20 pies de materiales para el marco exterior de la ventana, ¿cuál es el tamaño máximo de la ventana que puede crear? Use r para representar el radio del semicírculo.
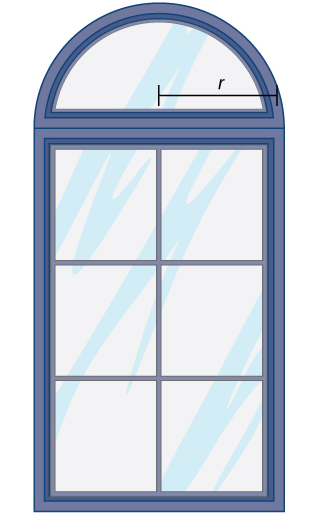
-
Tienes una hilera de jardín de 20 plantas de sandía que producen un promedio de 30 sandías cada una. Por cada planta de sandía adicional que se plante, la producción por planta de sandía disminuye en una sandía. ¿Cuántas plantas de sandía adicionales deberías plantar?
-
Estás construyendo una caja para que duerma tu gato. El material de felpa para la base cuadrada de la caja cuesta $5/pie²
 $2/pie². Necesitas una caja con un volumen de 4 pies³. Encuentra las dimensiones de la caja que minimicen el costo. Usa x para representar la longitud del lado de la caja.
$2/pie². Necesitas una caja con un volumen de 4 pies³. Encuentra las dimensiones de la caja que minimicen el costo. Usa x para representar la longitud del lado de la caja. -
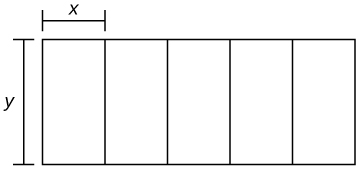
Estás construyendo cinco corrales idénticos adyacentes entre sí con un área total de 1000 m², como se muestra en la siguiente figura. ¿Qué dimensiones debes usar para minimizar la cantidad de valla?


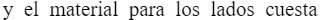 $2/pie². Necesitas una caja con un volumen de 4 pies³. Encuentra las dimensiones de la caja que minimicen el costo. Usa x para representar la longitud del lado de la caja.
$2/pie². Necesitas una caja con un volumen de 4 pies³. Encuentra las dimensiones de la caja que minimicen el costo. Usa x para representar la longitud del lado de la caja.
¡Hurra! Por fin encontré una página web desde donde soy capaz de obtener genuinamente datos útiles sobre mi estudio y así obtener más conocimiento.