| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.10 |

10.10 Longitud de arco y curvatura

Objetivos de aprendizaje:

10.10.1 Determine la longitud de la trayectoria de una partícula en el espacio utilizando la función de longitud de arco.
10.10.2 Explica el significado de la curvatura de una curva en el espacio y establece su fórmula.
10.10.3 Describa el significado de los vectores normales y binormales de una curva en el espacio.

En esta sección, estudiamos fórmulas relacionadas con curvas en dos y tres dimensiones, y vemos cómo están relacionadas con varias propiedades de la misma curva. Por ejemplo, supongamos que una función de valor vectorial describe el movimiento de una partícula en el espacio. Nos gustaría determinar qué tan lejos ha viajado la partícula en un intervalo de tiempo determinado, que puede describirse por la longitud del arco de la ruta que sigue. O suponga que la función de valor vectorial describe una carretera que estamos construyendo y queremos determinar qué tan bruscamente se curva la carretera en un punto dado. Esto se describe por la curvatura de la función en ese punto. Exploramos cada uno de estos conceptos en esta sección.

Longitud de arco para funciones vectoriales

Hemos visto cómo una función de valor vectorial describe una curva en dos o tres dimensiones. Recuerde las fórmulas alternativas para la curvatura, que establece que la fórmula para la longitud del arco de una curva definida por las funciones paramétricas x = x (t), y = y (t), t₁ ≤ t ≤ t₂ viene dada por

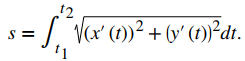
De manera similar, si definimos una curva suave usando una función de valor vectorial r (t) = f (t) i + g (t) j, donde a ≤ t ≤ b, la longitud del arco viene dada por la fórmula

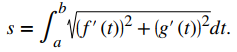
En tres dimensiones, si la función de valor vectorial se describe por r (t) = f (t) i + g (t) j + h (t) k durante el mismo intervalo a ≤ t ≤ b, se da la longitud del arco por

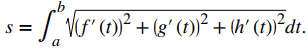
Teorema 10.10.1 Fórmulas de longitud de arco

1. Curva plana: Dada una curva suave C definida por la función \( \mathbf{r}(t) = f(t) \mathbf{i} + g(t) \mathbf{j} \), donde t se encuentra dentro del intervalo \( [a, b] \), la longitud del arco de C sobre el intervalo es \[ s = \displaystyle \int_a^b \sqrt{[f'(t)]^2 + [g'(t)]^2} \, dt = \displaystyle \int_a^b \|\mathbf{r}'(t)\| \, dt. \hspace{20pt} \text{(Ecuación 10.10.1)}\]
2. Curva espacial: Dada una curva suave C definida por la función \( \mathbf{r}(t) = f(t) \mathbf{i} + g(t) \mathbf{j} + h(t) \mathbf{k} \), donde t se encuentra dentro del intervalo \( [a, b] \), la longitud del arco de C sobre el intervalo es \[ s = \displaystyle \int_a^b \sqrt{[f'(t)]^2 + [g'(t)]^2 + [h'(t)]^2} \, dt = \displaystyle \int_a^b \|\mathbf{r}'(t)\| \, dt. \hspace{20pt} \text{(Ecuación 10.10.2)}\]

♦

Las dos fórmulas son muy similares; solo difieren en el hecho de que una curva espacial tiene tres funciones componentes en lugar de dos. Tenga en cuenta que las fórmulas se definen para curvas suaves: curvas donde la función de valor vectorial r(t) es diferenciable con una derivada distinta de cero. La condición de suavidad garantiza que la curva no tenga cúspides (o esquinas) que puedan hacer que la fórmula sea problemática.

Ejemplo ilustrativo 10.10_1. Encontrar la longitud del arco

Calcula la longitud del arco para cada una de las siguientes funciones vectoriales:

1. \( \mathbf{r}(t) = (3t – 2) \mathbf{i} + (4t + 5) \mathbf{j} \), \( 1 \leq t \leq 5 \)
2. \( \mathbf{r}(t) = \langle t \cos t, t \sin t, 2t \rangle \), \( 0 \leq t \leq 2\pi \)

Solución:

1. Usando la primera ecuación del Teorema 10.10.1, r′(t) = 3i + 4j, entonces

b. Usando la segunda ecuación del Teorema 10.10.1, r ′ (t) = ⟨cost − tsent, sent + tcost, 2⟩, entonces

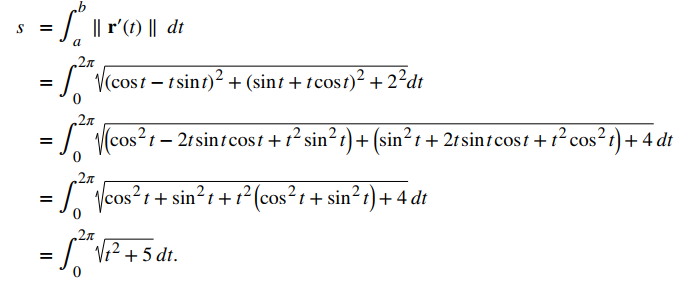
Aquí podemos usar una fórmula de integración de tablas

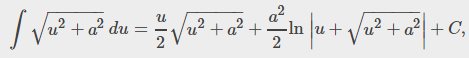
entonces obtenemos

♦

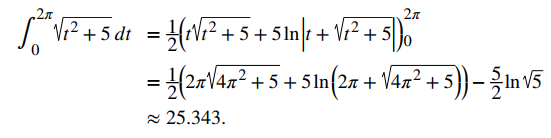
Ejercicio de control 10.10.1

Calcula la longitud del arco de la curva parametrizada \( \mathbf{r}(t) = \langle 2t^2 + 1, 2t^2 – 1, t^3 \rangle, 0 \leq t \leq 3. \) ♦

       Ahora volvemos a la hélice presentada anteriormente en este capítulo. Una función de valor vectorial que describe una hélice se puede escribir en la forma

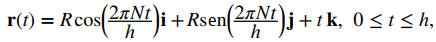
donde R representa el radio de la hélice, h representa la altura (distancia entre dos giros consecutivos) y la hélice completa N giros. Derivemos una fórmula para la longitud del arco de esta hélice usando la segunda ecuación del Teorema 10.10.1. Ante todo,

Por lo tanto,

Esto proporciona una fórmula para la longitud de un cable necesario para formar una hélice con N vueltas que tiene radio R y altura h.

Parametrización de longitud de arco

Ahora tenemos una fórmula para la longitud del arco de una curva definida por una función vectorial. Avancemos un paso más y examinemos qué es una función de longitud de arco.

Si una función de valor vectorial representa la posición de una partícula en el espacio como una función del tiempo, entonces la función de longitud de arco mide qué tan lejos viaja esa partícula en función del tiempo. La fórmula para la función de longitud de arco se sigue directamente de la fórmula para la longitud de arco:

\[ s(t) = \int_a^t \sqrt{(f'(u))^2 + (g'(u))^2 + (h'(u))^2} \, du. \hspace{20pt} \text{(Ecuación 10.10.3)}\]

Si la curva tiene dos dimensiones, solo aparecen dos términos debajo de la raíz cuadrada dentro de la integral. La razón para usar la variable independiente u es distinguir entre el tiempo y la variable de integración. Dado que s(t) mide la distancia recorrida en función del tiempo, s‘(t) mide la velocidad de la partícula en un momento dado. Como tenemos una fórmula para s(t) en la ecuación 10.10.3, podemos diferenciar ambos lados de la ecuación:

Si suponemos que r(t) define una curva suave, entonces la longitud del arco siempre aumenta, por lo que s ′(t) > 0 para t > a. Por último, si r(t) es una curva en la que ∥ r ′(t) ∥ = 1 para todo t, entonces

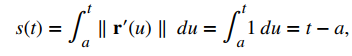
lo que significa que t representa la longitud del arco siempre que a = 0.

Teorema 10.10.2 Función de longitud de arco

Sea \( \mathbf{r}(t) \) describir una curva suave para \( t \geq a \). Entonces, la función longitud de arco está dada por

\[s(t) = \displaystyle \int_a^t \|\mathbf{r}'(u)\| \, du.\]

Además, \( \frac{ds}{dt} = \|\mathbf{r}'(t)\| > 0 \). Si \( \|\mathbf{r}'(t)\| = 1 \) para todo \( t \geq a \), entonces el parámetro t representa la longitud del arco desde el punto inicial en \( t = a \). ♦

Una aplicación útil de este teorema es encontrar una parametrización alternativa de una curva dada, llamada una parametrización de longitud de arco. Recuerda que cualquier función vectorial puede ser reparametrizada mediante un cambio de variables. Por ejemplo, si tenemos una función \( \mathbf{r}(t) = \langle 3\cos t, 3\sin t \rangle, 0 \leq t \leq 2\pi \) que parametriza un círculo de radio 3, podemos cambiar el parámetro de t a 4t, obteniendo una nueva parametrización \( \mathbf{r}(t) = \langle 3\cos 4t, 3\sin 4t \rangle \). La nueva parametrización sigue definiendo un círculo de radio 3, pero ahora solo necesitamos usar los valores \( 0 \leq t \leq \pi/2 \) para recorrer el círculo una vez.

Supongamos que encontramos la función de longitud de arco s(t) y somos capaces de resolver esta función para t como una función de s. Luego podemos volver a parametrizar la función original r(t) sustituyendo la expresión por t nuevamente en r(t). La función de valor vectorial ahora se escribe en términos del parámetro s. Como la variable s representa la longitud del arco, llamamos a esto una parametrización de la función original r(t). Una ventaja de encontrar la parametrización de longitud de arco es que la distancia recorrida a lo largo de la curva a partir de s = 0 ahora es igual al parámetro s. La parametrización de longitud de arco también aparece en el contexto de la curvatura (que examinaremos más adelante en esta sección) y las integrales de línea, que estudiamos en la Introducción al cálculo vectorial.

Ejemplo ilustrativo 10.10_2. Encontrar una parametrización de longitud de arco

Encuentra la parametrización de la longitud de arco para cada una de las siguientes curvas:

1. \( \mathbf{r}(t) = 4\cos t \mathbf{i} + 4\sin t \mathbf{j} \), \( t \geq 0 \)
2. \( \mathbf{r}(t) = \langle t + 3, 2t – 4, 2t \rangle \), \( t \geq 3 \)

Solución:
1. Primero encontramos la función de longitud de arco usando la Ecuación del Teorema 10.10.2:

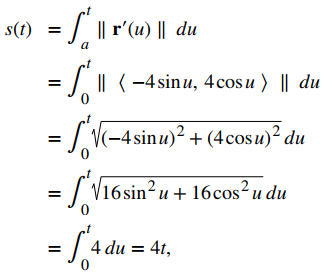
que da la relación entre la longitud del arco s y el parámetro t como s = 4t; entonces, t = s / 4. A continuación, reemplazamos la variable t en la función original r (t) = 4cost i + 4sent j con la expresión s / 4 para obtener

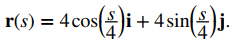
Esta es la parametrización de longitud de arco de r (t). Como la restricción original en t fue dada por t ≥ 0, la restricción en s se convierte en s / 4 ≥ 0, o s ≥ 0.

2. La función de longitud de arco viene dada por la ecuación dada en el Teorema 10.10.2:

Por lo tanto, la relación entre la longitud del arco s y el parámetro t es \( s = 3t – 9 \), así que \( t = \frac{s}{3} + 3 \). Sustituyendo esto en la función original \( \mathbf{r}(t) = \langle t + 3, 2t – 4, 2t \rangle \) se obtiene

\[ \mathbf{r}(s) = \left\langle \left(\frac{s}{3} + 3\right) + 3, 2\left(\frac{s}{3} + 3\right) – 4, 2\left(\frac{s}{3} + 3\right) \right\rangle = \left\langle \frac{s}{3} + 6, \frac{2s}{3} + 2, \frac{2s}{3} + 6 \right\rangle. \]

Esta es una parametrización de la longitud de arco de \( \mathbf{r}(t) \). La restricción original sobre el parámetro t era \( t \geq 3 \), así que la restricción sobre s es \( \frac{s}{3} + 3 \geq 3 \), o \( s \geq 0 \). ♦

Ejercicio de control 10.10.2

Encuentra la función de longitud de arco para la hélice

\[\mathbf{r}(t) = \langle 3\cos t, 3\sin t, 4t \rangle, t \geq 0.\]

Luego, usa la relación entre la longitud de arco y el parámetro t para encontrar una parametrización de longitud de arco de \( \mathbf{r}(t) \). ♦

Curvatura

Un tema importante relacionado con la longitud del arco es la curvatura. El concepto de curvatura proporciona una manera de medir cuán bruscamente gira una curva suave. Un círculo tiene una curvatura constante. Cuanto más pequeño es el radio del círculo, mayor es la curvatura.

Piensa en conducir por una carretera. Supongamos que el camino se encuentra en un arco de una gran circunferencia. En este caso, apenas tendría que girar la rueda para mantenerse en el camino. Ahora suponga que el radio es más pequeño. En este caso, deberá girar más bruscamente para mantenerse en el camino. En el caso de una curva que no sea una circunferencia, a menudo es útil primero inscribir una circunferencia en la curva en un punto dado para que sea tangente a la curva en ese punto y “abrace” la curva lo más cerca posible en un vecindad del punto (Figura 10.10_1). La curvatura del gráfico en ese punto se define entonces como la curvatura de la circunferencia inscrita.

Figura 10.10_1 El gráfico representa la curvatura de una función y = f (x). Cuanto más nítido es el giro en el gráfico, mayor es la curvatura y menor es el radio de la circunferencia inscrita.

Definición 10.10.1. Curvatura

Sea C una curva suave en el plano o en el espacio dada por \( \mathbf{r}(s) \), donde s es el parámetro de longitud de arco. La curvatura \( \kappa \) en s está dada por

\[\kappa = \left\| \frac{d\mathbf{T}}{ds} \right\| = \|\mathbf{T}'(s)\|.\]

♦

La fórmula en la definición de curvatura no es muy útil en términos de cálculo. En particular, recuerde que T(t) representa el vector unitario tangente a una función de valor vectorial dado r(t), y la fórmula para T(t) es

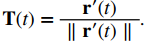
Para usar la fórmula de curvatura, primero es necesario expresar r(t) en términos del parámetro de longitud de arco s, luego encontrar el vector tangente unitario T(s) para la función r(s), luego tomar la derivada de T(s) con respecto a s. Este es un proceso tedioso. Afortunadamente, hay fórmulas equivalentes para la curvatura.

Teorema 10.10.3 Fórmulas alternativas para la curvatura

Si C es una curva suave dada por \( \mathbf{r}(t) \), entonces la curvatura \( \kappa \) de C en t está dada por

\[\kappa = \frac{\|\mathbf{T}'(t)\|}{\|\mathbf{r}'(t)\|}. \hspace{20pt} \text{(Ecuación 10.10.4)}\]

Si C es una curva tridimensional, entonces la curvatura puede estar dada por la fórmula

\[\kappa = \frac{\|\mathbf{r}'(t) \times \mathbf{r}”(t)\|}{\|\mathbf{r}'(t)\|^3}. \hspace{20pt} \text{(Ecuación 10.10.5)}\]

Si C es la gráfica de una función \( y = f(x) \) y existen \( y’ \) e \( y” \), entonces la curvatura \( \kappa \) en el punto \( (x, y) \) está dada por

\[\kappa = \frac{|y”|}{[1 + (y’)^2]^{3/2}}. \hspace{20pt} \text{(Ecuación 10.10.6)}\]

♦

Prueba:

La primera fórmula se sigue directamente de la regla de la cadena:

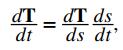
donde s es la longitud del arco a lo largo de la curva C. Dividiendo ambos lados por ds / dt, y tomando la magnitud de ambos lados da

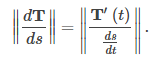
Como ds / dt = ∥ r ′ (t) ∥, esto proporciona la fórmula para la curvatura κ de una curva C en términos de cualquier parametrización de C:

En el caso de una curva tridimensional, comenzamos con las fórmulas T (t) = (r ′ (t)) / ∥ r ′ (t) ∥  y  ds / dt = ∥ r ′ (t) ∥. Por lo tanto, r ‘(t) = (ds / dt) T (t). Podemos tomar la derivada de esta función usando la fórmula del producto escalar:

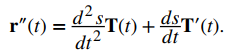
Usando estas dos últimas ecuaciones obtenemos

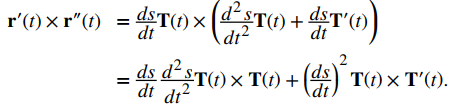
Como T (t) × T (t) = 0, esto se reduce a

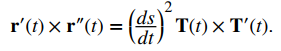
Como T ‘es paralelo a N y T es ortogonal a N, se deduce que T y T ‘ son ortogonales. Esto significa que ∥T × T ′∥ = ∥T∥∥T ′∥ sen (π / 2) = ∥T ′∥, entonces

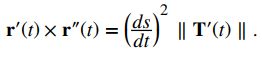
Ahora resolvemos esta ecuación para ∥T ′ (t) ∥ y usamos el hecho de que ds / dt = ∥ r ′ (t) ∥:

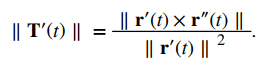
Luego, dividimos ambos lados entre ∥ r ′ (t) ∥. Esto da

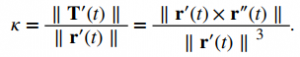
Esto prueba la primera ecuación del Teorema. Para probar la segunda ecuación, comenzamos con el supuesto de que la curva C está definida por la función y = f (x). Entonces, podemos definir r (t) = xi + f (x) j + 0k. Usando la fórmula anterior para la curvatura:

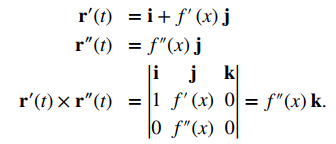
Por lo tanto,

♦

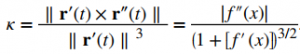
EJEMPLO ILUSTRATIVO 10.10_3. Encontrar una curvatura

Encuentre la curvatura para cada una de las siguientes curvas en el punto dado:

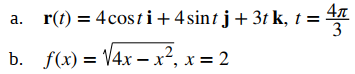
Solución:
a. Esta función describe una hélice.

La curvatura de la hélice en t = (4π) / 3 se puede encontrar usando la primera ecuación del Teorema 10.10.3. Primero, calcule T (t):

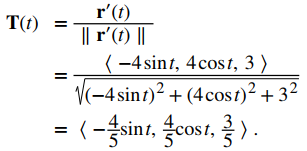
A continuación, calcule T ′ (t):

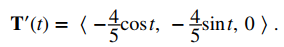
Por último, aplique la primera fórmula del teorema:

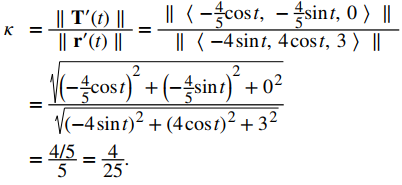
La curvatura de esta hélice es constante en todos los puntos de la hélice.

b. Esta función describe una semicircunferencia:

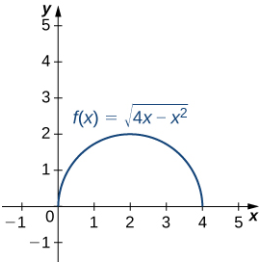
Para encontrar la curvatura de este gráfico, debemos usar la segunda ecuación del teorema 10.10.3. Primero, calculamos y′  e y″:

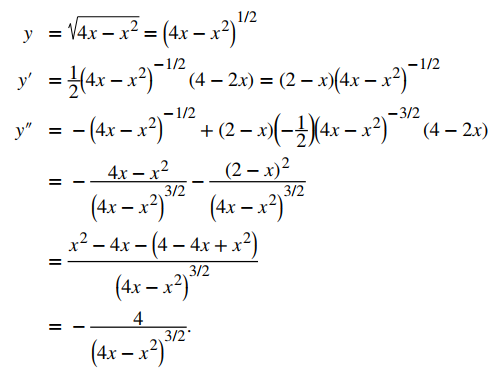
Luego, aplicamos la tercera ecuación del Teorema 10.140.3:

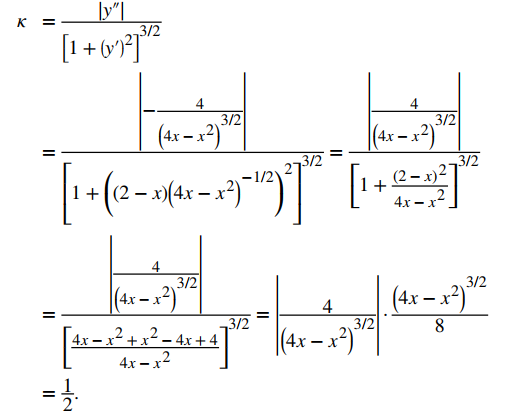
La curvatura de esta circunferencia es igual al recíproco de su radio. Hay un problema menor con el valor absoluto en la segunda ecuación del Teorema 10.10.3; sin embargo, una mirada más cercana al cálculo revela que el denominador es positivo para cualquier valor de x. ♦

Ejercicio de control 10.10.3

Encuentra la curvatura de la curva definida por la función

\[y = 3x^2 – 2x + 4\]

en el punto \( x = 2 \). ♦

Los vectores normales y binormales

Hemos visto que la derivada r′(t) de una función vectorial es un vector tangente a la curva definida por r(t), y la unidad de vector tangente T(t) puede calcularse dividiendo r′(t) por su magnitud. Al estudiar el movimiento en tres dimensiones, otros dos vectores son útiles para describir el movimiento de una partícula a lo largo de un camino en el espacio: el vector normal de la unidad principal y el vector binormal.

Definición 10.10.2. Vector normal y el vector binormal

Sea C una curva suave tridimensional representada por \( \mathbf{r} \) sobre un intervalo abierto I. Si \( \mathbf{T}'(t) \neq \mathbf{0} \), entonces el vector normal unitario principal en t se define como

\[ \mathbf{N}(t) = \frac{\mathbf{T}'(t)}{\|\mathbf{T}'(t)\|}. \hspace{20pt} \text{(Ecuación …)}\]

El vector binormal en t se define como

\[ \mathbf{B}(t) = \mathbf{T}(t) \times \mathbf{N}(t), \hspace{20pt} \text{(Ecuación …)}\]

donde \( \mathbf{T}(t) \) es el vector tangente unitario. ♦

Tenga en cuenta que, por definición, el vector binormal es ortogonal tanto al vector tangente unitario como al vector normal. Además, B(t) es siempre un vector unitario. Esto se puede mostrar usando la fórmula para la magnitud de un producto cruz

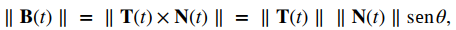
donde θ es el ángulo entre T(t) y N(t). Como N(t) es la derivada de un vector unitario, la propiedad (vii) de la derivada de una función con valor vectorial nos dice que T(t) y N(t) son ortogonales entre sí, por lo que θ = π / 2 . Además, ambos son vectores unitarios, por lo que su magnitud es 1. Por lo tanto, ∥T(t) ∥∥N(t) ∥senθ = (1) (1) sen(π / 2) = 1 y B(t) es un vector unitario.

 

El vector normal unitario principal puede ser difícil de calcular porque el vector tangente unitario implica un cociente, y este cociente a menudo tiene una raíz cuadrada en el denominador. En el caso tridimensional, encontrar el producto cruz del vector tangente unitario y el vector normal unitario puede ser aún más engorroso. Afortunadamente, tenemos fórmulas alternativas para encontrar estos dos vectores, y se presentan en el próximo capítulo “Movimiento en el espacio”.

EJEMPLO ILUSTRATIVO 10.10_4. Encontrar el vector normal unitario principal y el vector binormal

Para cada una de las siguientes funciones con valores vectoriales, encuentre el vector normal de la unidad principal. Luego, si es posible, encuentre el vector binormal.

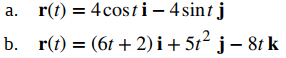
Solución:
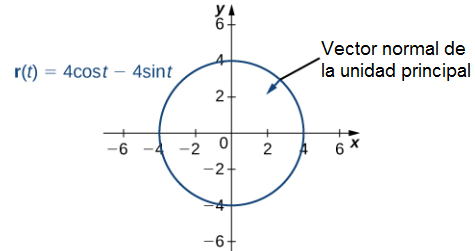
a. Esta función describe una circunferencia.

Para encontrar el vector normal de la unidad principal, primero debemos encontrar la unidad del vector tangente T (t):

A continuación, usamos la ecuación dada en la definición:

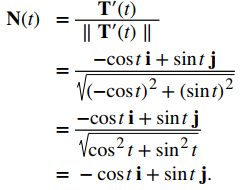
Observe que el vector tangente unitario y el vector normal unitario principal son ortogonales entre sí para todos los valores de t:

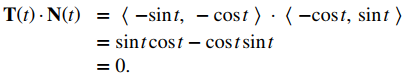
Además, el vector normal de la unidad principal apunta hacia el centro del círculo desde cada punto de la circunferencia. Dado que r (t) define una curva en dos dimensiones, no podemos calcular el vector binormal.

b. Esta función se ve así:

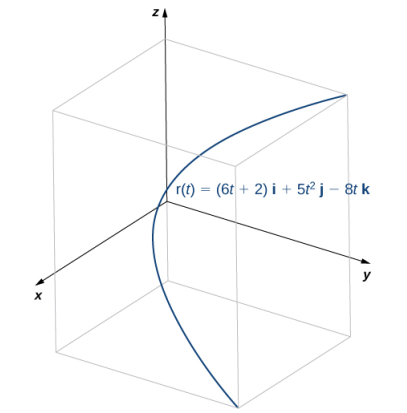
Para encontrar el vector normal de la unidad principal, primero encontramos el vector tangente unitario T (t):

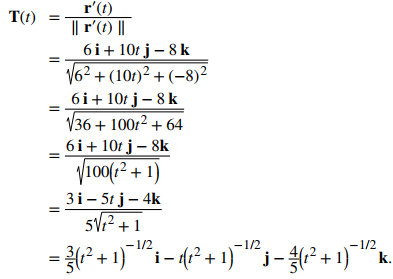
A continuación, calculamos T′(t)  y  ∥ T′(t) ∥:

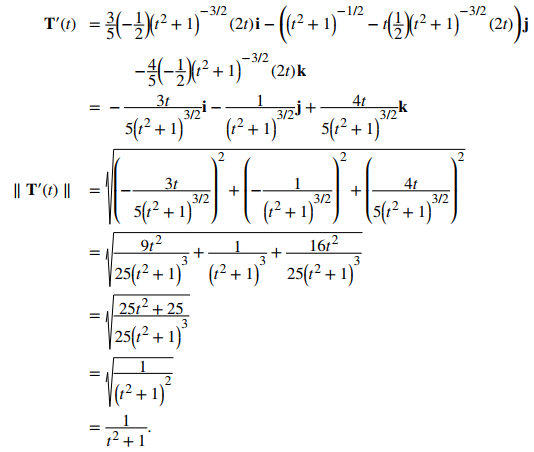
Por lo tanto, de acuerdo con la segunda ecuación en la definición:

Una vez más, el vector tangente unitario y el vector normal unitario principal son ortogonales entre sí para todos los valores de t:

Por último, dado que r (t) representa una curva tridimensional, podemos calcular el vector binormal utilizando la tercera ecuación dada en el Teorema 10.10.3:

♦

Ejercicio de control 10.10.4

Encuentra el vector normal unitario para la función vectorial \( \mathbf{r}(t) = (t^2 – 3t) \mathbf{i} + (4t + 1) \mathbf{j} \) y evalúalo en \( t = 2 \). ♦

       Para cualquier curva suave en tres dimensiones que esté definida por una función de valor vectorial, ahora tenemos fórmulas para el vector de tangente unitario T, el vector normal unitario N y el vector binormal B. El vector normal unitario y el vector binormal forman un plano que es perpendicular a la curva en cualquier punto de la curva, llamado plano normal. Además, estos tres vectores forman un marco de referencia en un espacio tridimensional llamado marco de referencia de Frenet (también llamado marco TNB) (Figura 10.10_2). El plano determinado por los vectores T y N forma el plano osculador de C en cualquier punto P de la curva.

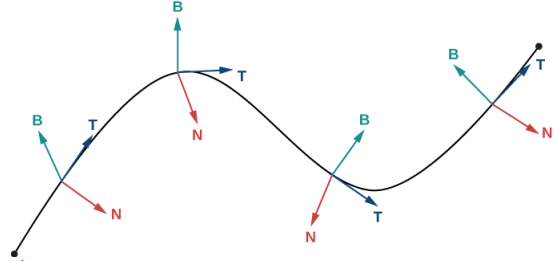
Figura 10.10_2 Esta figura representa un marco de referencia de Frenet. En cada punto P en una curva tridimensional, los vectores unidad tangente, unidad normal y binormal forman un marco de referencia tridimensional.

Supongamos que formamos un círculo en el plano osculador de C en el punto P de la curva. Suponga que el círculo tiene la misma curvatura que la curva en el punto P y deje que el círculo tenga un radio r. Luego, la curvatura del círculo viene dada por 1 / r. Llamamos r el radio de curvatura de la curva, y es igual al recíproco de la curvatura. Si este círculo se encuentra en el lado cóncavo de la curva y es tangente a la curva en el punto P, entonces este círculo se llama círculo osculador de C en P, como se muestra en la siguiente figura.

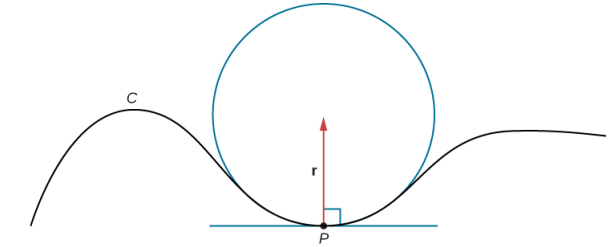
Figura 10.10_3 En este círculo osculador, el círculo es tangente a la curva C en el punto P y comparte la misma curvatura.

Para encontrar la ecuación de un círculo osculador en dos dimensiones, necesitamos encontrar solo el centro y el radio del círculo.

Ejemplo ilustrativo 10.10_5. Encontrar la ecuación de un círculo osculador

Encuentre la ecuación del círculo osculador de la hélice definida por la función y = x³ − 3x + 1 en x = 1.

Solución:
La figura 10.10_4 muestra la gráfica de y = x³ − 3x + 1.

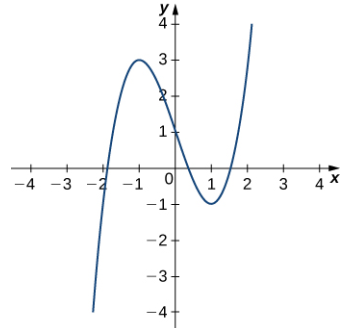
Figura 10.10_4 Queremos encontrar el círculo osculador de esta gráfica en el punto donde t = 1.

Primero, calculemos la curvatura en x = 1:

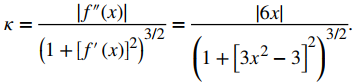
Esto da κ = 6. Por lo tanto, el radio del círculo osculador está dado por R = 1/κ = 1/6. Luego, calculamos las coordenadas del centro del círculo. Cuando x = 1, la pendiente de la recta tangente es cero. Por lo tanto, el centro del círculo osculador está directamente encima del punto en la gráfica con coordenadas (1, −1). El centro está ubicado en (1, −5/6). La fórmula para un círculo con radio r y centro (h, k) viene dada por (x − h)² + (y − k)² = r². Por lo tanto, la ecuación del círculo osculador es (x − 1)² + (y + 5/6)² = 1/36. La gráfica y su círculo osculador aparecen en la siguiente figura.

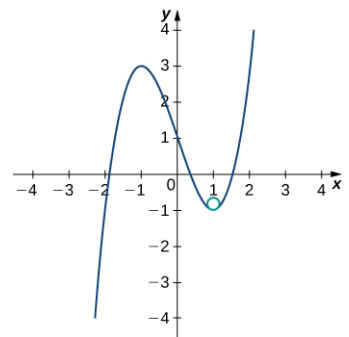
Figura 10.10_5 El círculo osculador tiene radio R = 1/6.

♦

Ejercicio de control 10.10.5

Encuentra la ecuación del círculo osculador de la curva definida por la función \( y = 3x^2 – 4x + 5 \) en \( x = 1 \). ♦