| 4. Aplicaciones de la derivada | Ejercicios propuestos para el Capítulo 4.8 |
4.8 LA REGLA DE L’HÔPITAL
Objetivos de aprendizaje:
4.8.1. Reconocer cuándo aplicar la regla de L′Hôpital.
4.8.2. Identificar formas indeterminadas producidas por cocientes, productos, sustracciones y potencias, y aplicar la regla de L’Hôpital en cada caso.
4.8.3. Describir las tasas de crecimiento relativo de las funciones.
En esta sección, examinamos una herramienta poderosa para evaluar límites. Esta herramienta, conocida como la regla de L’Hôpital, utiliza derivadas para calcular los límites. Con esta regla, podremos evaluar muchos límites que aún no hemos podido determinar. En lugar de confiar en la evidencia numérica para conjeturar que existe un límite, podremos demostrar definitivamente que existe un límite y determinar su valor exacto.
Aplicando la regla de L’Hôpital
La regla de L’Hôpital se puede utilizar para evaluar límites que involucran el cociente de dos funciones. Considere
\[\lim_{x\to a} \frac{f(x)}{g(x)}.\]
Si \(\lim_{x\to a} f(x) = L_1\) y \(\lim_{x\to a} g(x) = L_2 \ne 0\), entonces
\[\lim_{x\to a} \frac{f(x)}{g(x)} = \frac{L_1}{L_2}.\]
Sin embargo, ¿qué sucede si \(\lim_{x\to a} f(x) = 0\) y \(\lim_{x\to a} g(x) = 0\)? A esto lo llamamos una de las formas indeterminadas, de tipo \(\frac{0}{0}\). Esta se considera una forma indeterminada porque no podemos determinar el comportamiento exacto de \(\frac{f(x)}{g(x)}\) cuando \(x\) se acerca a \(a\) sin un análisis más profundo. Hemos visto ejemplos de esto anteriormente en el texto. Por ejemplo, considere
\[\lim_{x\to 2} \frac{x^2-4}{x-2} \quad \text{y} \quad \lim_{x\to 0} \frac{\sin x}{x}.\]
Para el primero de estos ejemplos, podemos evaluar el límite factorizando el numerador y escribiendo
\[\lim_{x\rightarrow2}\frac{x^{2}-4}{x-2}=\lim_{x\rightarrow2}\frac{(x+2)(x-2)}{x-2}=\lim_{x\rightarrow2}(x+2)=2+2=4.\]
Para \(\lim_{x\rightarrow0}\frac{\sin x}{x}\) pudimos demostrar, usando un argumento geométrico, que
\[\lim_{x\rightarrow0}\frac{\sin x}{x}=1.\]
Aquí usamos una técnica diferente para evaluar límites como estos. Esta técnica no solo proporciona una manera más fácil de evaluar estos límites, sino que también, y lo que es más importante, nos brinda una forma de evaluar muchos otros límites que no pudimos calcular previamente.
La idea detrás de la regla de L’Hôpital se puede explicar usando aproximaciones lineales locales. Considere dos funciones diferenciables \(f\) y \(g\) tales que \(\lim_{x\to a} f(x) = 0 = \lim_{x\to a} g(x)\) y tales que \(g'(a) \ne 0\). Para \(x\) cerca de \(a\), podemos escribir
\[f(x) \approx f(a) + f'(a)(x-a)\]
y
\[g(x) \approx g(a) + g'(a)(x-a).\]
Por lo tanto,
\[\frac{f(x)}{g(x)} \approx \frac{f(a) + f'(a)(x-a)}{g(a) + g'(a)(x-a)}.\]

Dado que \(f\) es diferenciable en \(a\), entonces \(f\) es continua en \(a\), y por lo tanto \(f(a) = \lim_{x\rightarrow a} f(x) = 0\). De manera similar, \(g(a) = \lim_{x\rightarrow a} g(x) = 0\). Si también asumimos que \(f’\) y \(g’\) son continuas en \(x = a\), entonces \(f'(a) = \lim_{x\rightarrow a} f'(x)\) y \(g'(a) = \lim_{x\rightarrow a} g'(x)\). Usando estas ideas, concluimos que
\[\lim_{x\rightarrow a} \frac{f(x)}{g(x)} = \lim_{x\rightarrow a} \frac{f'(x)(x-a)}{g'(x)(x-a)} = \lim_{x\rightarrow a} \frac{f'(x)}{g'(x)}.\]
Observe que la suposición de que \(f’\) y \(g’\) son continuas en \(a\) y \(g'(a) \ne 0\) se puede relajar. Enunciamos la regla de L’Hôpital formalmente para la forma indeterminada \(\frac{0}{0}\). También observe que la notación \(\frac{0}{0}\) no significa que realmente estemos dividiendo cero por cero. Más bien, estamos usando la notación \(\frac{0}{0}\) para representar un cociente de límites, cada uno de los cuales es cero.
Teorema 4..8.1. Regla de L’Hôpital (caso 0/0)
Suponga que \(f\) y \(g\) son funciones diferenciables en un intervalo abierto que contiene a \(a\), excepto posiblemente en \(a\). Si
\[\lim_{x\rightarrow a}f(x)=0 \quad \text{y} \quad \lim_{x\rightarrow a}g(x)=0,\]
entonces
\[\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f^{\prime}(x)}{g^{\prime}(x)}.\]
asumiendo que el límite de la derecha existe o es \(\infty\) o \(-\infty\). Este resultado también se cumple si estamos considerando límites laterales, o si \(a = \infty\) o \(-\infty\).
Prueba:
Proporcionamos una prueba de este teorema en el caso especial cuando \(f\), \(g\), \(f’\) y \(g’\) son todas continuas en un intervalo abierto que contiene a \(a\). En ese caso, dado que \(\lim_{x\to a} f(x) = 0 = \lim_{x\to a} g(x)\) y \(f\) y \(g\) son continuas en \(a\), se deduce que \(f(a) = 0 = g(a)\). Por lo tanto,
\[ \begin{aligned} \lim_{x\to a} \frac{f(x)}{g(x)} &= \lim_{x\to a} \frac{f(x) – f(a)}{g(x) – g(a)} & \text{ya que } f(a) = 0 = g(a) \\ &= \lim_{x\to a} \frac{\frac{f(x) – f(a)}{x-a}}{\frac{g(x) – g(a)}{x-a}} & \text{álgebra} \\ &= \frac{\lim_{x\to a} \frac{f(x) – f(a)}{x-a}}{\lim_{x\to a} \frac{g(x) – g(a)}{x-a}} & \text{límite de un cociente} \\ &= \frac{f'(a)}{g'(a)} & \text{definición de la derivada} \\ &= \frac{\lim_{x\to a} f'(x)}{\lim_{x\to a} g'(x)} & \text{continuidad de } f’ \text{ y } g’ \\ &= \lim_{x\to a} \frac{f'(x)}{g'(x)} & \text{límite de un cociente}. \end{aligned} \]
Observe que la regla de L’Hôpital establece que podemos calcular el límite de un cociente \(\frac{f}{g}\) considerando el límite del cociente de las derivadas \(\frac{f’}{g’}\). Es importante darse cuenta de que no estamos calculando la derivada del cociente \(\frac{f}{g}\).
Ejemplo ilustrativo 4.8.1: Aplicando la regla de L’Hôpital (caso 0/0)
Evalúe cada uno de los siguientes límites aplicando la regla de L’Hôpital.
a. \(\lim_{x\rightarrow0}\frac{1-\cos x}{x}\)
b. \(\lim_{x\rightarrow1}\frac{\sin(\pi x)}{\ln x}\)
c. \(\lim_{x\rightarrow\infty}\frac{e^{1/x}-1}{1/x}\)
d. \(\lim_{x\rightarrow0}\frac{\sin x-x}{x^{2}}\)
Solución:
Evalúe cada uno de los siguientes límites aplicando la regla de L’Hôpital.
a. Dado que el numerador \(1 – \cos x \rightarrow 0\) y el denominador \(x \rightarrow 0\), podemos aplicar la regla de L’Hôpital para evaluar este límite. Tenemos
\[ \begin{aligned} \lim_{x\rightarrow0}\frac{1-\cos x}{x} &= \lim_{x\rightarrow0}\frac{\frac{d}{dx}(1-\cos x)}{\frac{d}{dx}(x)} \\ &= \lim_{x\rightarrow0}\frac{\sin x}{1} \\ &= \frac{\lim_{x\rightarrow0}\sin x}{\lim_{x\rightarrow0}1} \\ &= \frac{0}{1} = 0. \end{aligned} \]
b. Cuando \(x \rightarrow 1\), el numerador \(\sin(\pi x) \rightarrow 0\) y el denominador \(\ln(x) \rightarrow 0\). Por lo tanto, podemos aplicar la regla de L’Hôpital. Obtenemos
\[ \begin{aligned} \lim_{x\rightarrow1}\frac{\sin(\pi x)}{\ln x} &= \lim_{x\rightarrow1}\frac{\pi\cos(\pi x)}{1/x} \\ &= \lim_{x\rightarrow1}x\pi\cos(\pi x) \\ &= (1 \cdot \pi) (-1) = -\pi. \end{aligned} \]
c. Cuando \(x \rightarrow \infty\), el numerador \(e^{1/x}-1 \rightarrow 0\) y el denominador \(\frac{1}{x} \rightarrow 0\). Por lo tanto, podemos aplicar la regla de L’Hôpital. Obtenemos
\[ \begin{aligned} \lim_{x\rightarrow\infty}\frac{e^{1/x}-1}{1/x} &= \lim_{x\rightarrow\infty}\frac{e^{1/x}\left(-\frac{1}{x^2}\right)}{\left(-\frac{1}{x^2}\right)} \\ &= \lim_{x\rightarrow\infty}e^{1/x} = e^0 = 1. \end{aligned} \]
d. Cuando \(x \rightarrow 0\), tanto el numerador como el denominador se acercan a cero. Por lo tanto, podemos aplicar la regla de L’Hôpital. Obtenemos
\[\lim_{x\rightarrow0}\frac{\sin x – x}{x^2} = \lim_{x\rightarrow0}\frac{\cos x – 1}{2x}.\]
Dado que el numerador y el denominador de este nuevo cociente se acercan a cero cuando \(x \rightarrow 0\), aplicamos la regla de L’Hôpital nuevamente. Al hacerlo, vemos que
\[\lim_{x\rightarrow0}\frac{\cos x – 1}{2x} = \lim_{x\rightarrow0}\frac{-\sin x}{2} = 0.\]
Por lo tanto, concluimos que
\[\lim_{x\rightarrow0}\frac{\sin x – x}{x^2} = 0.\]
♦
Ejercicio de control 4.8.1
Evalúe \(\lim_{x\rightarrow0}\frac{x}{\tan x}\). ♦
También podemos usar la regla de L’Hôpital para evaluar límites de cocientes \(\frac{f(x)}{g(x)}\) en los que \(f(x) \rightarrow \pm\infty\) y \(g(x) \rightarrow \pm\infty\). Los límites de esta forma se clasifican como formas indeterminadas de tipo \(\frac{\infty}{\infty}\). Nuevamente, observe que en realidad no estamos dividiendo \(\infty\) por \(\infty\). Dado que \(\frac{\infty}{\infty}\) no es un número real, eso es imposible; más bien, \(\frac{\infty}{\infty}\) se usa para representar un cociente de límites, cada uno de los cuales es \(\infty\) o \(-\infty\).
Teorema 4.8.2. Regla de L’Hôpital (caso ∞/∞)
Para el caso \( \frac{\infty}{\infty} \), supongamos que \( f(x) \) y \( g(x) \) son funciones diferenciables en un intervalo abierto que contiene a \( a \), excepto posiblemente en \( a \). Si se cumple que: \[ \lim_{x \to a} f(x) = \infty \quad \text{o} \quad \lim_{x \to a} f(x) = -\infty, \] y \[ \lim_{x \to a} g(x) = \infty \quad \text{o} \quad \lim_{x \to a} g(x) = -\infty, \] entonces, bajo la condición de que el límite de la razón de las derivadas exista, se tiene: \[ \lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)}. \] Si el límite en la derecha existe o tiende a \( \infty \) o \( -\infty \), se puede aplicar la regla de L’Hôpital. Esta regla también es válida cuando el límite es infinito o cuando se considera \( x \to \infty \) o \( x \to -\infty \), o cuando el límite es unilateral.♦
Ejemplo ilustrativo 4.8.2: Aplicando la regla de L’Hôpital (caso ∞/∞)
Evalúe cada uno de los siguientes límites aplicando la regla de L’Hôpital.
a. \(\lim_{x\rightarrow\infty}\frac{3x+5}{2x+1}\)
b. \(\lim_{x\rightarrow0^{+}}\frac{\ln x}{\cot x}\)
Solución:
a. Dado que \(3x+5\) y \(2x+1\) son polinomios de primer grado con coeficientes principales positivos, \(\lim_{x\rightarrow\infty}(3x+5)=\infty\) y \(\lim_{x\rightarrow\infty}(2x+1)=\infty\). Por lo tanto, aplicamos la regla de L’Hôpital y obtenemos
\[\lim_{x\rightarrow\infty}\frac{3x+5}{2x+1}=\lim_{x\rightarrow\infty}\frac{3}{2}=\frac{3}{2}.\]
Observe que este límite también se puede calcular sin invocar la regla de L’Hôpital. Anteriormente en el capítulo, mostramos cómo evaluar tal límite dividiendo el numerador y el denominador por la mayor potencia de x en el denominador. Al hacerlo, vimos que
\[\lim_{x\rightarrow\infty}\frac{3x+5}{2x+1}=\lim_{x\rightarrow\infty}\frac{3+5/x}{2+1/x}=\frac{3}{2}.\]
La regla de L’Hôpital nos proporciona un medio alternativo para evaluar este tipo de límite.
b. Aquí, \(\lim_{x\rightarrow0^{+}}\ln x=-\infty\) y \(\lim_{x\rightarrow0^{+}}\cot x=\infty\). Por lo tanto, podemos aplicar la regla de L’Hôpital y obtener
\[\lim_{x\rightarrow0^{+}}\frac{\ln x}{\cot x}=\lim_{x\rightarrow0^{+}}\frac{1/x}{-\csc^{2}x}=\lim_{x\rightarrow0^{+}}\frac{-\sin^{2}x}{x}.\]
Ahora, cuando \(x\rightarrow0^{+}\), \(\csc^{2}x\rightarrow\infty\). Por lo tanto, el primer término en el denominador se acerca a cero y el segundo término se hace muy grande. En tal caso, cualquier cosa puede suceder con el producto. Por lo tanto, no podemos sacar ninguna conclusión todavía. Para evaluar el límite, usamos la definición de csc para escribir
\[\lim_{x\rightarrow0^{+}}\frac{1}{-x\csc^{2}x}=\lim_{x\rightarrow0^{+}}\frac{\sin^{2}x}{-x}.\]
Ahora, \(\lim_{x\rightarrow0^{+}}\sin^{2}x=0\) y \(\lim_{x\rightarrow0^{+}}x=0\), así que aplicamos la regla de L’Hôpital nuevamente. Encontramos que
\[\lim_{x\rightarrow0^{+}}\frac{\sin^{2}x}{-x}=\lim_{x\rightarrow0^{+}}\frac{2\sin x\cos x}{-1}=\frac{0}{-1}=0.\]
Concluimos que
\[\lim_{x\rightarrow0^{+}}\frac{\ln x}{\cot x}=0.\]
♦
Ejercicio de control 4.8.2
Evalúe \(\lim_{x\rightarrow\infty}\frac{\ln x}{5x}\). ♦
Como se mencionó, la regla de L’Hôpital es una herramienta extremadamente útil para evaluar límites. Sin embargo, es importante recordar que para aplicar la regla de L’Hôpital a un cociente \(\frac{f(x)}{g(x)}\), es esencial que el límite de \(\frac{f(x)}{g(x)}\) sea de la forma \(\frac{0}{0}\) o \(\infty/\infty\). Considere el siguiente ejemplo.
Ejemplo ilustrativo 4.8.3: Cuándo no se puede aplicar la regla de L’Hôpital
Considere \(\lim_{x\rightarrow1}\frac{x^{2}+5}{3x+4}\). Muestre que el límite no se puede evaluar aplicando la regla de L’Hôpital.
Soluciòn:
Dado que los límites del numerador y el denominador no son ambos cero y no son ambos infinitos, no podemos aplicar la regla de L’Hôpital. Si intentamos hacerlo, obtenemos
\[\frac{d}{dx}(x^2+5)=2x\]
y
\[\frac{d}{dx}(3x+4)=3.\]
En cuyo punto concluiríamos erróneamente que
\[\lim_{x\rightarrow1}\frac{x^2+5}{3x+4}=\lim_{x\rightarrow1}\frac{2x}{3}=\frac{2}{3}.\]
Sin embargo, dado que \(\lim_{x\rightarrow1}(x^2+5)=6\) y \(\lim_{x\rightarrow1}(3x+4)=7\), en realidad tenemos
\[\lim_{x\rightarrow1}\frac{x^2+5}{3x+4}=\frac{6}{7}.\]
Podemos concluir que
\[\lim_{x\rightarrow1}\frac{x^2+5}{3x+4}\ne\lim_{x\rightarrow1}\frac{\frac{d}{dx}(x^2+5)}{\frac{d}{dx}(3x+4)}. \]
♦
Ejercicio de control 4.8.3
Explique por qué no podemos aplicar la regla de L’Hôpital para evaluar \(\lim_{x\rightarrow0^{+}}\frac{\cos x}{x}\). Evalúe \(\lim_{x\rightarrow0^{+}}\frac{\cos x}{x}\) por otros medios. ♦
Otras formas indeterminadas
La regla de L’Hôpital es muy útil para evaluar los límites que involucran las formas indeterminadas 0/0 y ∞/∞. Sin embargo, también podemos usar la regla de L’Hôpital para ayudar a evaluar los límites que involucran otras formas indeterminadas que surgen al evaluar los límites.
Las expresiones 0⋅∞, ∞ − ∞, 1∞, ∞0 y 00 se consideran formas indeterminadas. Estas expresiones no son números reales. Más bien, representan formas que surgen cuando se intenta evaluar ciertos límites. A continuación veremos por qué son formas indeterminadas y luego mostramos cómo usar la regla de L’Hôpital en estos casos. La idea clave es que debemos reescribir las formas indeterminadas de tal manera que lleguemos a la forma indeterminada 0/0 o ∞/∞.
Forma indeterminada de tipo 0⋅∞
Supongamos que queremos evaluar lim x → a (f (x) ⋅ g (x)), donde f (x) → 0 y g (x) → ∞ (o −∞) cuando x → a. Dado que un término en el producto se acerca a cero pero el otro término se está volviendo arbitrariamente grande (en magnitud), cualquier cosa puede pasarle al producto. Usamos la notación 0⋅∞ para denotar la forma que surge en esta situación. La expresión 0⋅∞ se considera indeterminada porque no podemos determinar sin un análisis más detallado el comportamiento exacto del producto f (x) ⋅ g (x) cuando x → a.
Por ejemplo, sea n un número entero positivo y considere
\( f(x) = \frac{1}{(x^n + 1)} \) y \( g(x) = 3x^2 \).
Cuando \( x \rightarrow \infty \), \( f(x) \rightarrow 0 \) y \( g(x) \rightarrow \infty \). Sin embargo, el límite cuando \( x \rightarrow \infty \) de \( f(x)g(x) = \frac{3x^2}{(x^n + 1)} \) varía, dependiendo de \( n \). Si \( n = 2 \), entonces \( \lim_{x \to \infty} f(x)g(x) = 3 \). Si \( n = 1 \), entonces \( \lim_{x \to \infty} f(x)g(x) = \infty \). Si \( n = 3 \), entonces \( \lim_{x \to \infty} f(x)g(x) = 0 \). Aquí consideramos otro límite que involucra la forma indeterminada \( 0 \cdot \infty \) y mostramos cómo reescribir la función como un cociente para usar la regla de L’Hôpital.
Ejemplo ilustrativo 4.8.4: Forma indeterminada del tipo 0 ⋅ ∞
Evaluar \( \lim_{x \to 0^+} x \ln x \).
Solución:
Primero, reescribimos la función \( x \ln x \) como un cociente para aplicar la regla de L’Hôpital. Si escribimos
\( x \ln x = \frac{\ln x}{1/x}, \)
vemos que \( \ln x \rightarrow -\infty \) cuando \( x \rightarrow 0^+ \) y \( \frac{1}{x} \rightarrow \infty \) cuando \( x \rightarrow 0^+ \). Por lo tanto, podemos aplicar la regla de L’Hôpital y obtener
\( \lim_{x \to 0^+} \frac{\ln x}{1/x} = \lim_{x \to 0^+} \frac{\frac{d}{dx}(\ln x)}{\frac{d}{dx}(1/x)} = \lim_{x \to 0^+} \frac{1/x}{-1/x^2} = \lim_{x \to 0^+} (-x) = 0. \)
Concluimos que
\( \lim_{x \to 0^+} x \ln x = 0. \)
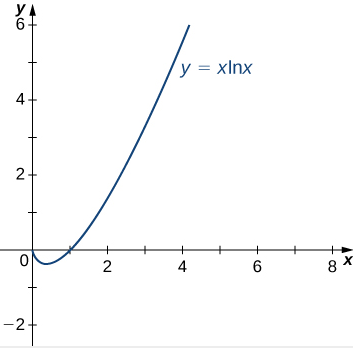
Figura 4.8.2 Encontrando el límite en x = 0 de la función f (x) = xlnx.
♦
Ejercicio de control 4.8.4
Evaluar \( \lim_{x \to 0} x \cot x \). ♦
Forma indeterminada de tipo ∞ − ∞
Otro tipo de forma indeterminada es ∞ − ∞. Considere el siguiente ejemplo. Sea n un número entero positivo y sea f (x) = 3xn y g (x) = 3x2 + 5. Cuando x → ∞, f (x) → ∞ y g (x) → ∞. Estamos interesados en lim x → ∞ (f (x) − g (x)). Dependiendo de si f (x) crece más rápido, g (x) crece más rápido o crecen a la misma velocidad, como vemos a continuación, cualquier cosa puede suceder en este límite. Dado que f (x) → ∞ y g (x) → ∞, escribimos ∞ − ∞ para denotar la forma de este límite. Al igual que con nuestras otras formas indeterminadas, ∞ − ∞ no tiene significado por sí solo y debemos hacer más análisis para determinar el valor del límite. Por ejemplo, suponga que el exponente n en la función f (x) = 3xn es n = 3, entonces

Por otro lado, si n = 2, entonces
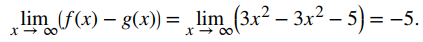
Sin embargo, si n = 1, entonces

Por lo tanto, el límite no puede determinarse considerando únicamente ∞ − ∞.
A continuación, veremos cómo reescribir una expresión que involucra la forma indeterminada ∞ − ∞ como una fracción para aplicar la regla de L’Hôpital.
Ejemplo ilustrativo 4.8.5: Forma indeterminada del tipo ∞ − ∞
Evaluar \( \lim_{x \to 0^+} \left( \frac{1}{x^2} – \frac{1}{\tan x} \right) \).
Solución:
Al combinar las fracciones, podemos escribir la función como un cociente. Dado que el mínimo común denominador es \(x^2 \tan x\), tenemos
\( \frac{1}{x^2} – \frac{1}{\tan x} = \frac{\tan x – x^2}{x^2 \tan x}. \)
Cuando \(x \to 0^+\), el numerador \( \tan x – x^2 \to 0 \) y el denominador \( x^2 \tan x \to 0 \). Por lo tanto, podemos aplicar la regla de L’Hôpital. Tomando las derivadas del numerador y el denominador, tenemos
\( \lim_{x \to 0^+} \frac{\tan x – x^2}{x^2 \tan x} = \lim_{x \to 0^+} \frac{\sec^2 x – 2x}{x^2 \sec^2 x + 2x \tan x}. \)
Cuando \(x \to 0^+\), \( (\sec^2 x) – 2x \to 1 \) y \( x^2 \sec^2 x + 2x \tan x \to 0 \). Dado que el denominador es positivo cuando \(x\) se acerca a cero desde la derecha, concluimos que
\( \lim_{x \to 0^+} \frac{\sec^2 x – 2x}{x^2 \sec^2 x + 2x \tan x} = \infty. \)
Por lo tanto,
\( \lim_{x \to 0^+} \left( \frac{1}{x^2} – \frac{1}{\tan x} \right) = \infty. \)
♦
Ejercicio de control 4.8.5
Evaluar \( \lim_{x \to 0^+} \left( \frac{1}{x} – \frac{1}{\sin x} \right) \). ♦
Otro tipo de forma indeterminada que surge al evaluar los límites involucra exponentes.
Formas indeterminadas 00, ∞0 y 1∞
Las expresiones 00, ∞0 y 1∞ son todas formas indeterminadas. Por sí solas, estas expresiones no tienen sentido porque en realidad no podemos evaluar estas expresiones como evaluaríamos una expresión que involucra números reales. Más bien, estas expresiones representan formas que surgen al encontrar límites. En los videos para los “Ejercicios resueltos” de esta sección examinamos cómo se puede usar la regla de L’Hôpital para evaluar los límites que involucran estas formas indeterminadas.
Dado que la regla de L’Hôpital se aplica a los cocientes, utilizamos la función de logaritmo natural y sus propiedades para reducir un problema al evaluar un límite que involucra exponentes a un problema relacionado que involucra un límite de un cociente.
Por ejemplo, supongamos que queremos evaluar lim x → a f (x) g (x) y llegamos a la forma indeterminada ∞0.
(Las formas indeterminadas 00 y 1∞ pueden manejarse de manera similar.)
Procedemos de la siguiente manera.
Sea

Entonces,

Por lo tanto

Como lim x → a f (x) = ∞, sabemos que lim x → a ln (f (x)) = ∞. Por lo tanto, lim x → a g (x) ln (f (x)) es de la forma indeterminada 0⋅∞, y podemos usar las técnicas discutidas anteriormente para reescribir la expresión g (x) ln (f (x)) en una forma para que podamos aplicar la regla de L’Hôpital.
Supongamos que lim x → a g (x) ln (f (x)) = L, donde L puede ser ∞ o −∞. Luego

Como la función de logaritmo natural es continua, concluimos que

lo que nos da

Ejemplo ilustrativo 4.8.6: Forma indeterminada del tipo ∞⁰
Evaluar \( \lim_{x \to \infty} x^{1/x} \).
Solución:
Sea \( y = x^{1/x} \). Entonces,
\( \ln(x^{1/x}) = \frac{1}{x} \ln x = \frac{\ln x}{x}. \)
Necesitamos evaluar \( \lim_{x \to \infty} \frac{\ln x}{x} \). Aplicando la regla de L’Hôpital, obtenemos
\( \lim_{x \to \infty} \ln y = \lim_{x \to \infty} \frac{\ln x}{x} = \lim_{x \to \infty} \frac{1/x}{1} = 0. \)
Por lo tanto, \( \lim_{x \to \infty} \ln y = 0 \). Dado que la función logaritmo natural es continua, concluimos que
\( \ln \left( \lim_{x \to \infty} y \right) = 0, \)
lo que lleva a
\( \lim_{x \to \infty} y = \lim_{x \to \infty} \frac{\ln x}{x} = e^0 = 1. \)
Por lo tanto,
\( \lim_{x \to \infty} x^{1/x} = 1. \)
♦
Ejercicio de control 4.8.6
Evaluar \( \lim_{x \to \infty} x^{1/\ln(x)} \). ♦
Ejemplo ilustrativo 4.8.7: Forma indeterminada del tipo 0⁰
Evaluar \( \lim_{x \to 0^+} x^{\sin x} \).
Solución:
Sea
\( y = x^{\sin x}. \)
Por lo tanto,
\( \ln y = \ln(x^{\sin x}) = \sin x \ln x. \)
Ahora evaluamos \( \lim_{x \to 0^+} \sin x \ln x \). Dado que \( \lim_{x \to 0^+} \sin x = 0 \) y \( \lim_{x \to 0^+} \ln x = -\infty \), tenemos la forma indeterminada \( 0 \cdot \infty \). Para aplicar la regla de L’Hôpital, necesitamos reescribir \( \sin x \ln x \) como una fracción. Podríamos escribir
\( \sin x \ln x = \frac{\sin x}{1/\ln x} \)
o
\( \sin x \ln x = \frac{\ln x}{1/\sin x} = \frac{\ln x}{\csc x}. \)
Consideremos la primera opción. En este caso, aplicando la regla de L’Hôpital, obtendríamos
\( \lim_{x \to 0^+} \sin x \ln x = \lim_{x \to 0^+} \frac{\sin x}{1/\ln x} = \lim_{x \to 0^+} \frac{\cos x}{-1/(x(\ln x)^2)} = \lim_{x \to 0^+} (-x(\ln x)^2 \cos x). \)
Desafortunadamente, no solo tenemos otra expresión que involucra la forma indeterminada \( 0 \cdot \infty \), sino que el nuevo límite es aún más complicado de evaluar que con el que empezamos. En cambio, probamos con la segunda opción. Escribiendo
\( \sin x \ln x = \frac{\ln x}{1/\sin x} = \frac{\ln x}{\csc x}, \)
y aplicando la regla de L’Hôpital, obtenemos
\( \lim_{x \to 0^+} \sin x \ln x = \lim_{x \to 0^+} \frac{\ln x}{\csc x} = \lim_{x \to 0^+} \frac{1/x}{-\csc x \cot x} = \lim_{x \to 0^+} \frac{-1}{x \csc x \cot x}. \)
Usando el hecho de que \( \csc x = \frac{1}{\sin x} \) y \( \cot x = \frac{\cos x}{\sin x} \), podemos reescribir la expresión del lado derecho como
\( \lim_{x \to 0^+} \frac{-\sin^2 x}{x \cos x} = \lim_{x \to 0^+} \left[ \frac{\sin x}{x} \cdot (-\tan x) \right] = \left( \lim_{x \to 0^+} \frac{\sin x}{x} \right) \cdot \left( \lim_{x \to 0^+} (-\tan x) \right) = 1 \cdot 0 = 0. \)
Concluimos que \( \lim_{x \to 0^+} \ln y = 0 \). Por lo tanto, \( \ln \left( \lim_{x \to 0^+} y \right) = 0 \) y tenemos
\( \lim_{x \to 0^+} y = \lim_{x \to 0^+} x^{\sin x} = e^0 = 1. \)
Por lo tanto,
\( \lim_{x \to 0^+} x^{\sin x} = 1. \)
♦
Ejercicio de control 4.8.7
Evaluar \( \lim_{x \to 0^+} x^x \). ♦
Tasas de crecimiento de funciones
Suponga que las funciones f y g se aproximan al infinito cuando x → ∞. Aunque los valores de ambas funciones se vuelven arbitrariamente grandes a medida que los valores de x se vuelven lo suficientemente grandes, a veces una función crece más rápidamente que la otra. Por ejemplo, las funciones polinomiales f (x) = x2 y g (x) = x3 ambas tienden al infinito cuando x → ∞. Sin embargo, como se muestra en la siguiente tabla, los valores de x3 están creciendo mucho más rápido que los valores de x2.
| x | 10 | 100 | 1000 | 10,000 |
| f (x) = x2 | 100 | 10,000 | 1,000,000 | 100,000,000 |
| g (x) = x3 | 1000 | 1,000,000 | 1,000,000,000 | 1,000,000,000,000 |
Tabla 4.8.1 Comparación de las tasas de crecimiento de x2 y x3
De hecho,

Como resultado, decimos que x3 está creciendo más rápidamente que x2 cuando x → ∞.
Por otro lado, para f (x) = x2 y g (x) = 3x2 + 4x + 1, aunque los valores de g (x) son siempre mayores que los valores de f (x) para x > 0, cada valor de g (x) es aproximadamente tres veces el valor correspondiente de f (x) cuando x → ∞, como se muestra en la siguiente tabla.
De hecho,

| x | 10 | 100 | 1000 | 10,000 |
| f (x) = x2 | 100 | 10,000 | 1,000,000 | 100,000,000 |
| g (x) = 3x2 + 4x + 1 | 341 | 30,401 | 3,004,001 | 300,040,001 |
Tabla 4.8.2 Comparación de las tasas de crecimiento de x2 y 3x2 + 4x + 1
En este caso, decimos que x2 y 3x2 + 4x + 1 están creciendo a la misma tasa cuando x → ∞.
Más generalmente, suponga que f y g son dos funciones que se aproximan al infinito cuando x → ∞. Decimos que g crece más rápidamente que f como x → ∞ si

Por otro lado, si existe una constante M ≠ 0 tal que

decimos que f y g crecen a la misma razón cuando x → ∞.
A continuación, veremos cómo usar la regla de L’Hôpital para comparar las tasas de crecimiento de las funciones potencia, exponencial y logarítmica.
Ejemplo ilustrativo 4.8.8: Comparando las tasas de crecimiento de ln(x), x² y eˣ
Para cada uno de los siguientes pares de funciones, usa la regla de L’Hôpital para evaluar \( \lim_{x \to \infty} \left( \frac{f(x)}{g(x)} \right) \).
- \( f(x) = x^2 \) y \( g(x) = e^x \)
- \( f(x) = \ln(x) \) y \( g(x) = x^2 \)
Solución:
a. Dado que \( \lim_{x \to \infty} x^2 = \infty \) y \( \lim_{x \to \infty} e^x = \infty \), podemos usar la regla de L’Hôpital para evaluar \( \lim_{x \to \infty} \left[ \frac{x^2}{e^x} \right] \). Obtenemos
\( \lim_{x \to \infty} \frac{x^2}{e^x} = \lim_{x \to \infty} \frac{2x}{e^x}. \)
Dado que \( \lim_{x \to \infty} 2x = \infty \) y \( \lim_{x \to \infty} e^x = \infty \), podemos aplicar la regla de L’Hôpital nuevamente. Dado que
\( \lim_{x \to \infty} \frac{2x}{e^x} = \lim_{x \to \infty} \frac{2}{e^x} = 0, \)
concluimos que
\( \lim_{x \to \infty} \frac{x^2}{e^x} = 0. \)
Por lo tanto, \( e^x \) crece más rápidamente que \( x^2 \) cuando \( x \to \infty. \)
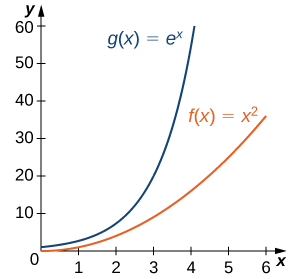
Figura 4.8.3 Una función exponencial crece a una tasa más rápida que una función potencia.
| \(x\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \(x^2\) | 25 | 100 | 225 | 400 |
| \(e^x\) | 148 | 22,026 | 3,269,017 | 485,165,195 |
Tabla 4.8.3 Tasas de crecimiento de una función potencia y una función exponencial.
b. Dado que \( \lim_{x \to \infty} \ln x = \infty \) y \( \lim_{x \to \infty} x^2 = \infty \), podemos usar la regla de L’Hôpital para evaluar \( \lim_{x \to \infty} \frac{\ln x}{x^2} \). Obtenemos
\( \lim_{x \to \infty} \frac{\ln x}{x^2} = \lim_{x \to \infty} \frac{1/x}{2x} = \lim_{x \to \infty} \frac{1}{2x^2} = 0. \)
Por lo tanto, \( x^2 \) crece más rápidamente que \( \ln x \) cuando \( x \to \infty. \)
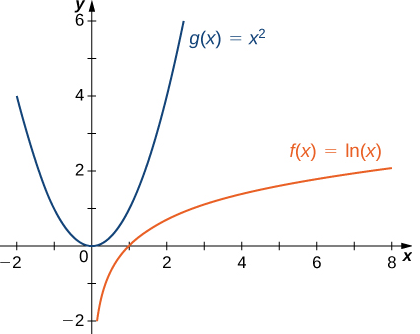
Figura 4.8.4. Una función potencia crece a una tasa más rápida que una función logarítmica.
| \(x\) | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| \( \ln(x) \) | 2.303 | 4.605 | 6.908 | 9.210 |
| \(x^2\) | 100 | 10,000 | 1,000,000 | 100,000,000 |
Tabla 4.8.4. Tasas de crecimiento de una función potencia y una función logarítmica. ♦
Ejercicio de control 4.8.8
Compare las tasas de crecimiento de \( x^{100} \) y \( 2^x \). ♦
Usando las mismas ideas que en el Ejemplo 4.8.8a, no es difícil demostrar que eˣ crece más rápidamente que xᵖ para cualquier p > 0. En la Figura 4.8.5 y la Tabla 4.8.5, comparamos eˣ con x³ y x⁴ cuando x → ∞.
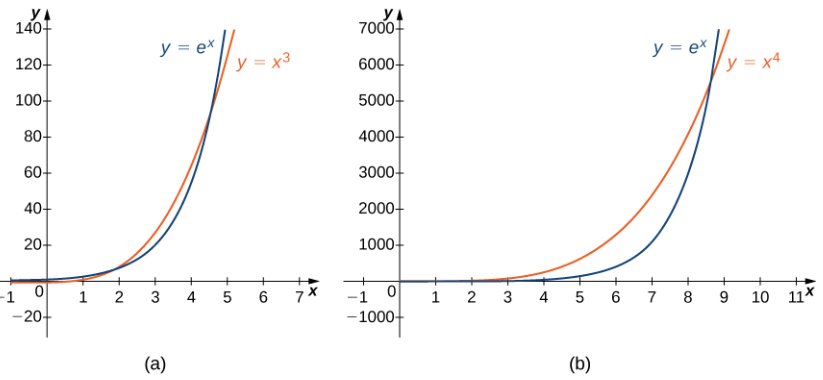
Figura 4.8.5. La función exponencial eˣ crece más rápido que xᵖ para cualquier p > 0.
(a) Comparación de eˣ con x³.
(b) Comparación de eˣ con x⁴.
| \(x\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \(x^3\) | 125 | 1000 | 3375 | 8000 |
| \(x^4\) | 625 | 10,000 | 50,625 | 160,000 |
| \(e^x\) | 148 | 22,026 | 3,269,017 | 485,165,195 |
Tabla 4.8.5. Una función exponencial crece a una tasa más rápida que cualquier función potencia.
De manera similar, no es difícil demostrar que \( x^p \) crece más rápidamente que \( \ln x \) para cualquier \( p > 0 \). En la Figura 4.8.6 y la Tabla 4.8.6, comparamos \( \ln x \) con \( \sqrt[3]{x} \) y \( \sqrt{x} \).
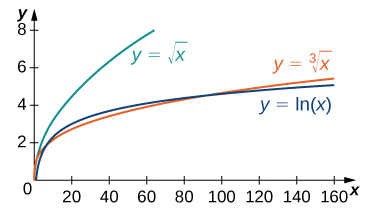
Figura 4.8.6. La función y = ln(x) crece más lentamente que xᵖ para cualquier p > 0 cuando x → ∞.
| \(x\) | 10 | 100 | 1000 | 10,000 |
|---|---|---|---|---|
| \( \ln(x) \) | 2.303 | 4.605 | 6.908 | 9.210 |
| \( \sqrt[3]{x} \) | 2.154 | 4.642 | 10 | 21.544 |
| \( \sqrt{x} \) | 3.162 | 10 | 31.623 | 100 |
Tabla 4.8.6. Una función logarítmica crece a una tasa más lenta que cualquier función raíz.

supongamos que sabemos que f'(x) es una función continua. Use la regla de Lhopital para mostrar que:
log_(x→0)〖(f(x+h)-f(x-h))/2h〗=f'(x)