| 10.3 El producto punto |

Ejercicios propuestos para el Capitulo 10.3

        Para los siguientes ejercicios, se dan los vectores u y v. Calcule el producto punto u⋅v:

123. \(\mathbf{u} = \langle 3, 0 \rangle\), \(\mathbf{v} = \langle 2, 2 \rangle\)
124. \(\mathbf{u} = \langle 3, -4 \rangle\), \(\mathbf{v} = \langle 4, 3 \rangle\)
125. \(\mathbf{u} = \langle 2, 2, -1 \rangle\), \(\mathbf{v} = \langle -1, 2, 2 \rangle\)
126. \(\mathbf{u} = \langle 4, 5, -6 \rangle\), \(\mathbf{v} = \langle 0, -2, -3 \rangle\)

      Para los siguientes ejercicios, se dan los vectores a, b, y c. Determine los vectores (a⋅b)c y (a⋅c)b. Exprese los vectores en forma de componentes:

127. \(\mathbf{a} = \langle 2, 0, -3 \rangle\), \(\mathbf{b} = \langle -4, -7, 1 \rangle\), \(\mathbf{c} = \langle 1, 1, -1 \rangle\)
128. \(\mathbf{a} = \langle 0, 1, 2 \rangle\), \(\mathbf{b} = \langle -1, 0, 1 \rangle\), \(\mathbf{c} = \langle 1, 0, -1 \rangle\)
129. \(\mathbf{a} = \mathbf{i} + \mathbf{j}\), \(\mathbf{b} = \mathbf{i} – \mathbf{k}\), \(\mathbf{c} = \mathbf{i} – 2\mathbf{k}\)
130. \(\mathbf{a} = \mathbf{i} – \mathbf{j} + \mathbf{k}\), \(\mathbf{b} = \mathbf{j} + 3\mathbf{k}\), \(\mathbf{c} = -\mathbf{i} + 2\mathbf{j} – 4\mathbf{k}\)

Para los siguientes ejercicios, se dan los vectores bidimensionales \(\mathbf{a}\) y \(\mathbf{b}\).

1. Encuentre la medida del ángulo \(\theta\) entre \(\mathbf{a}\) y \(\mathbf{b}\). Exprese la respuesta en radianes redondeado a dos decimales, si no es posible expresarlo exactamente.
2. ¿Es \(\theta\) un ángulo agudo?

131. \(\mathbf{a} = \langle 3, -1 \rangle\), \(\mathbf{b} = \langle -4, 0 \rangle\)
132. \(\mathbf{a} = \langle 2, 1 \rangle\), \(\mathbf{b} = \langle -1, 3 \rangle\)
133. \(\mathbf{u} = 3\mathbf{i}\), \(\mathbf{v} = 4\mathbf{i} + 4\mathbf{j}\)
134. \(\mathbf{u} = 5\mathbf{i}\), \(\mathbf{v} = -6\mathbf{i} + 6\mathbf{j}\)

Para los siguientes ejercicios, encuentre la medida del ángulo entre los vectores tridimensionales \(\mathbf{a}\) y \(\mathbf{b}\). Exprese la respuesta en radianes redondeado a dos decimales, si no es posible expresarla exactamente.

135. \(\mathbf{a} = \langle 3, -1, 2 \rangle\), \(\mathbf{b} = \langle 1, -1, -2 \rangle\)
136. \(\mathbf{a} = \langle 0, -1, -3 \rangle\), \(\mathbf{b} = \langle 2, 3, -1 \rangle\)
137. \(\mathbf{a} = \mathbf{i} + \mathbf{j}\), \(\mathbf{b} = \mathbf{j} – \mathbf{k}\)
138. \(\mathbf{a} = \mathbf{i} – 2\mathbf{j} + \mathbf{k}\), \(\mathbf{b} = \mathbf{i} + \mathbf{j} – 2\mathbf{k}\)
139. [T] \(\mathbf{a} = 3\mathbf{i} – \mathbf{j} – 2\mathbf{k}\), \(\mathbf{b} = \mathbf{v} + \mathbf{w}\), donde \(\mathbf{v} = -2\mathbf{i} – 3\mathbf{j} + 2\mathbf{k}\) y \(\mathbf{w} = \mathbf{i} + 2\mathbf{k}\)
140. [T] \(\mathbf{a} = 3\mathbf{i} – \mathbf{j} + 2\mathbf{k}\), \(\mathbf{b} = \mathbf{v} – \mathbf{w}\), donde \(\mathbf{v} = 2\mathbf{i} + \mathbf{j} + 4\mathbf{k}\) y \(\mathbf{w} = 6\mathbf{i} + \mathbf{j} + 2\mathbf{k}\)

Para los siguientes ejercicios, determine si los vectores dados son ortogonales.

141. \(\mathbf{a} = \langle x, y \rangle\), \(\mathbf{b} = \langle -y, x \rangle\), donde \(x\) y \(y\) son números reales no nulos
142. \(\mathbf{a} = \langle x, x \rangle\), \(\mathbf{b} = \langle -y, y \rangle\), donde \(x\) y \(y\) son números reales no nulos
143. \(\mathbf{a} = 3\mathbf{i} – \mathbf{j} – 2\mathbf{k}\), \(\mathbf{b} = -2\mathbf{i} – 3\mathbf{j} + \mathbf{k}\)
144. \(\mathbf{a} = \mathbf{i} – \mathbf{j}\), \(\mathbf{b} = 7\mathbf{i} + 2\mathbf{j} – \mathbf{k}\)

145. Encuentre todos los vectores bidimensionales \(\mathbf{a}\) ortogonales al vector \(\mathbf{b} = \langle 3, 4 \rangle\). Exprese la respuesta en forma de componentes.
146. Encuentre todos los vectores bidimensionales \(\mathbf{a}\) ortogonales al vector \(\mathbf{b} = \langle 5, -6 \rangle\). Exprese la respuesta usando vectores unitarios estándar.
147. Determine todos los vectores tridimensionales \(\mathbf{u}\) ortogonales al vector \(\mathbf{v} = \langle 1, 1, 0 \rangle\). Exprese la respuesta usando vectores unitarios estándar.
148. Determine todos los vectores tridimensionales \(\mathbf{u}\) ortogonales al vector \(\mathbf{v} = \mathbf{i} – \mathbf{j} – \mathbf{k}\). Exprese la respuesta en forma de componentes.
149. Determine el número real \(\alpha\) tal que los vectores \(\mathbf{a} = 2\mathbf{i} + 3\mathbf{j}\) y \(\mathbf{b} = 9\mathbf{i} + \alpha \mathbf{j}\) sean ortogonales.
150. Determine el número real \(\alpha\) tal que los vectores \(\mathbf{a} = -3\mathbf{i} + 2\mathbf{j}\) y \(\mathbf{b} = 2\mathbf{i} + \alpha \mathbf{j}\) sean ortogonales.

151. [T] Considere los puntos \(P(4, 5)\) y \(Q(5, -7)\).
     1. Determine los vectores \(\overrightarrow{OP}\) y \(\overrightarrow{OQ}\). Exprese la respuesta usando vectores unitarios estándar.
     2. Determine la medida del ángulo \(O\) en el triángulo \(OPQ\). Exprese la respuesta en grados redondeado a dos decimales.
152. [T] Considere los puntos \(A(1, 1)\), \(B(2, -7)\), y \(C(6, 3)\).
     1. Determine los vectores \(\overrightarrow{BA}\) y \(\overrightarrow{BC}\). Exprese la respuesta en forma de componentes.
     2. Determine la medida del ángulo \(B\) en el triángulo \(ABC\). Exprese la respuesta en grados redondeado a dos decimales.

153. Determine la medida del ángulo \(A\) en el triángulo \(ABC\), donde \(A(1, 1, 8)\), \(B(4, -3, -4)\), y \(C(-3, 1, 5)\). Exprese su respuesta en grados redondeado a dos decimales.
154. Considere los puntos \(P(3, 7, -2)\) y \(Q(1, 1, -3)\). Determine el ángulo entre los vectores \(\overrightarrow{OP}\) y \(\overrightarrow{OQ}\). Exprese la respuesta en grados redondeado a dos decimales.

Para los siguientes ejercicios, determine qué pares (si los hay) de los siguientes vectores son ortogonales.

155. \(\mathbf{u} = \langle 3, 7, -2 \rangle\), \(\mathbf{v} = \langle 5, -3, -3 \rangle\), \(\mathbf{w} = \langle 0, 1, -1 \rangle\)
156. \(\mathbf{u} = \mathbf{i} – \mathbf{k}\), \(\mathbf{v} = 5\mathbf{j} – 5\mathbf{k}\), \(\mathbf{w} = 10\mathbf{j}\)

157. Use vectores para mostrar que un paralelogramo con diagonales iguales es un rectángulo.
158. Use vectores para mostrar que las diagonales de un rombo son perpendiculares.
159. Muestre que \(\mathbf{u} \cdot (\mathbf{v} + \mathbf{w}) = \mathbf{u} \cdot \mathbf{v} + \mathbf{u} \cdot \mathbf{w}\) es cierto para cualesquiera vectores \(\mathbf{u}\), \(\mathbf{v}\), y \(\mathbf{w}\).
160. Verifique la identidad \(\mathbf{u} \cdot (\mathbf{v} + \mathbf{w}) = \mathbf{u} \cdot \mathbf{v} + \mathbf{u} \cdot \mathbf{w}\) para los vectores \(\mathbf{u} = \langle 1, 0, 4 \rangle\), \(\mathbf{v} = \langle -2, 3, 5 \rangle\), y \(\mathbf{w} = \langle 4, -2, 6 \rangle\).

Para los siguientes problemas, se da el vector \(\mathbf{u}\).

1. Encuentre los cosenos directores para el vector \(\mathbf{u}\).
2. Encuentre los ángulos directores para el vector \(\mathbf{u}\) expresados en grados. (Redondee la respuesta al entero más cercano).

161. \(\mathbf{u} = \langle 2, 2, 1 \rangle\)
162. \(\mathbf{u} = \mathbf{i} – 2\mathbf{j} + 2\mathbf{k}\)
163. \(\mathbf{u} = \langle -1, 5, 2 \rangle\)
164. \(\mathbf{u} = \langle 2, 3, 4 \rangle\)

165. Considere \(\mathbf{u} = \langle a, b, c \rangle\) un vector tridimensional no nulo. Sean \(\cos \alpha\), \(\cos \beta\), y \(\cos \gamma\) los cosenos directores de \(\mathbf{u}\). Muestre que \(\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma = 1\).
166. Determine los cosenos directores del vector \(\mathbf{u} = \mathbf{i} + 2\mathbf{j} + 2\mathbf{k}\) y muestre que satisfacen \(\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma = 1\).

Para los siguientes ejercicios, se dan los vectores \(\mathbf{u}\) y \(\mathbf{v}\).

1. Encuentre la proyección vectorial \(\mathbf{w} = \text{proj}_{\mathbf{u}} \mathbf{v}\) del vector \(\mathbf{v}\) sobre el vector \(\mathbf{u}\). Exprese su respuesta en forma de componentes.
2. Encuentre la proyección escalar \(\text{comp}_{\mathbf{u}} \mathbf{v}\) del vector \(\mathbf{v}\) sobre el vector \(\mathbf{u}\).

167. \(\mathbf{u} = 5\mathbf{i} + 2\mathbf{j}\), \(\mathbf{v} = 2\mathbf{i} + 3\mathbf{j}\)
168. \(\mathbf{u} = \langle -4, 7 \rangle\), \(\mathbf{v} = \langle 3, 5 \rangle\)
169. \(\mathbf{u} = 3\mathbf{i} + 2\mathbf{k}\), \(\mathbf{v} = 2\mathbf{j} + 4\mathbf{k}\)
170. \(\mathbf{u} = \langle 4, 4, 0 \rangle\), \(\mathbf{v} = \langle 0, 4, 1 \rangle\)

171. Considere los vectores \(\mathbf{u} = 4\mathbf{i} – 3\mathbf{j}\) y \(\mathbf{v} = 3\mathbf{i} + 2\mathbf{j}\).
     1. Encuentre la forma de componente del vector \(\mathbf{w} = \text{proj}_{\mathbf{u}} \mathbf{v}\) que representa la proyección de \(\mathbf{v}\) sobre \(\mathbf{u}\).
     2. Escriba la descomposición \(\mathbf{v} = \mathbf{w} + \mathbf{q}\) del vector \(\mathbf{v}\) en las componentes ortogonales \(\mathbf{w}\) y \(\mathbf{q}\), donde \(\mathbf{w}\) es la proyección de \(\mathbf{v}\) sobre \(\mathbf{u}\) y \(\mathbf{q}\) es un vector ortogonal a la dirección de \(\mathbf{u}\).
172. Considere los vectores \(\mathbf{u} = 2\mathbf{i} + 4\mathbf{j}\) y \(\mathbf{v} = 4\mathbf{j} + 2\mathbf{k}\).
     1. Encuentre la forma de componente del vector \(\mathbf{w} = \text{proj}_{\mathbf{u}} \mathbf{v}\) que representa la proyección de \(\mathbf{v}\) sobre \(\mathbf{u}\).
     2. Escriba la descomposición \(\mathbf{v} = \mathbf{w} + \mathbf{q}\) del vector \(\mathbf{v}\) en las componentes ortogonales \(\mathbf{w}\) y \(\mathbf{q}\), donde \(\mathbf{w}\) es la proyección de \(\mathbf{v}\) sobre \(\mathbf{u}\) y \(\mathbf{q}\) es un vector ortogonal a la dirección de \(\mathbf{u}\).
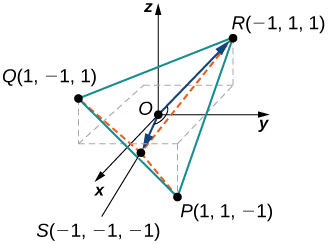
173. Una molécula de metano tiene un átomo de carbono situado en el origen y cuatro átomos de hidrógeno situados en los puntos \(P(1, 1, -1)\), \(Q(1, -1, 1)\), \(R(-1, 1, 1)\), y \(S(-1, -1, -1)\) (ver figura).
     1. Encuentre la distancia entre los átomos de hidrógeno situados en \(P\) y \(R\).
     2. Encuentre el ángulo entre los vectores \(\overrightarrow{OS}\) y \(\overrightarrow{OR}\) que conectan el átomo de carbono con los átomos de hidrógeno situados en \(S\) y \(R\), que también se llama el ángulo de enlace. Exprese la respuesta en grados redondeada a dos decimales.

174. [T] Encuentre los vectores que unen el centro de un reloj a las horas 1:00, 2:00 y 3:00. Suponga que el reloj es circular con un radio de 1 unidad.
175. Encuentre el trabajo realizado por la fuerza \(\mathbf{F} = \langle 5, 6, -2 \rangle\) (medido en Newtons) que mueve una partícula desde el punto \(P(3, -1, 0)\) al punto \(Q(2, 3, 1)\) a lo largo de una línea recta (la distancia se mide en metros).
176. [T] Un trineo es arrastrado ejerciendo una fuerza de 100 N en una cuerda que forma un ángulo de \(25^\circ\) con la horizontal. Encuentre el trabajo realizado al tirar del trineo 40 m. (Redondee la respuesta a un decimal).
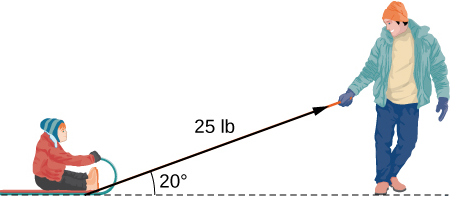
177. [T] Un padre está tirando de su hijo en un trineo en un ángulo de \(20^\circ\) con la horizontal con una fuerza de 25 lb (vea la siguiente imagen). Él tira del trineo en una trayectoria recta de 50 ft. ¿Cuánto trabajo realizó el hombre al tirar del trineo? (Redondee la respuesta al entero más cercano).

178. [T] Un automóvil es remolcado usando una fuerza de 1600 N. La cuerda usada para tirar del automóvil forma un ángulo de \(25^\circ\) con la horizontal. Encuentre el trabajo realizado al remolcar el automóvil 2 km. Exprese la respuesta en julios (\(1J = 1N \cdot m\)) redondeado al entero más cercano.
179. [T] Un barco navega hacia el norte ayudado por un viento que sopla en dirección N\(30^\circ\)E con una magnitud de 500 lb. ¿Cuánto trabajo realiza el viento mientras el barco se mueve 100 ft? (Redondee la respuesta a dos decimales).
180. El vector \(\mathbf{p} = \langle 150, 225, 375 \rangle\) representa el precio de ciertos modelos de bicicletas vendidas por una tienda de bicicletas. El vector \(\mathbf{n} = \langle 10, 7, 9 \rangle\) representa el número de bicicletas vendidas de cada modelo, respectivamente. Calcule el producto escalar \(\mathbf{p} \cdot \mathbf{n}\) y indique su significado.
181. [T] Dos fuerzas \(\mathbf{F}_1\) y \(\mathbf{F}_2\) están representadas por vectores con puntos iniciales que están en el origen. La primera fuerza tiene una magnitud de 20 lb y el punto terminal del vector es el punto \(P(1, 1, 0)\). La segunda fuerza tiene una magnitud de 40 lb y el punto terminal de su vector es el punto \(Q(0, 1, 1)\). Sea \(\mathbf{F}\) la fuerza resultante de las fuerzas \(\mathbf{F}_1\) y \(\mathbf{F}_2\).
     1. Encuentre la magnitud de \(\mathbf{F}\). (Redondee la respuesta a un decimal).
     2. Encuentre los ángulos directores de \(\mathbf{F}\). (Exprese la respuesta en grados redondeado a un decimal).

182. [T] Considere \(\mathbf{r}(t) = \langle \cos t, \sin t, 2t \rangle\) el vector de posición de una partícula en el tiempo \(t \in [0, 30]\), donde las componentes de \(\mathbf{r}\) se expresan en centímetros y el tiempo en segundos. Sea \(\overrightarrow{OP}\) el vector de posición de la partícula después de 1 segundo.
     1. Muestre que todos los vectores \(\overrightarrow{PQ}\), donde \(Q(x, y, z)\) es un punto arbitrario, son ortogonales al vector de velocidad instantánea \(\mathbf{v}(1)\) de la partícula después de 1 segundo, se puede expresar como \(\overrightarrow{PQ} = \langle x – \cos 1, y – \sin 1, z – 2 \rangle\), donde \(x \sin 1 – y \cos 1 – 2z + 4 = 0\). El conjunto de puntos \(Q\) describe un plano llamado el plano normal a la trayectoria de la partícula en el punto \(P\).
     2. Use un CAS para visualizar el vector de velocidad instantánea y el plano normal en el punto \(P\) junto con la trayectoria de la partícula.