| 8. Ecuaciones paramétricas y coordenadas polares | Ejercicios propuestos del Capítulo 8.3 |
8.3 Coordenadas polares
Objetivos de aprendizaje:
8.3.1. Ubique puntos en un plano usando coordenadas polares.
8.3.2. Convierte puntos entre coordenadas rectangulares y polares.
8.3.3. Dibuja curvas polares a partir de ecuaciones dadas.
8.3.4. Convierte ecuaciones entre coordenadas rectangulares y polares.
8.3.5. Identificar la simetría en curvas polares y ecuaciones.
El sistema de coordenadas rectangulares (o plano cartesiano) proporciona un medio para asignar puntos a pares ordenados y pares ordenados a puntos. Esto se llama mapeo uno a uno de puntos en el plano a pares ordenados. El sistema de coordenadas polares proporciona un método alternativo para asignar puntos a pares ordenados. En esta sección vemos que en algunas circunstancias, las coordenadas polares pueden ser más útiles que las coordenadas rectangulares.
Definición de coordenadas polares
Para encontrar las coordenadas de un punto en el sistema de coordenadas polares, considere la figura 8.3_1. El punto P tiene coordenadas cartesianas (x, y). El segmento de recta que conecta el origen con el punto P mide la distancia desde el origen hasta P y tiene una longitud r. El ángulo entre el eje x positivo y el segmento de recta mide θ. Esta observación sugiere una correspondencia natural entre el par de coordenadas (x, y) y los valores r y θ. Esta correspondencia es la base del sistema de coordenadas polares. Tenga en cuenta que cada punto en el plano cartesiano tiene dos valores (de ahí el término par ordenado) asociados. En el sistema de coordenadas polares, cada punto también tiene dos valores asociados: r y θ.
(Figura 8.3_1 Un punto arbitrario en el plano cartesiano.)
Usando trigonometría de triángulo rectángulo, las siguientes ecuaciones son verdaderas para el punto P:
cosθ = x/r entonces x = rcosθ
senθ = y/r entonces y = rsenθ.
Además,
r² = x² + y² y tanθ = y/x.
Por tanto, cada punto (x, y) del sistema de coordenadas cartesiano se puede representar como un par ordenado (r, θ) en el sistema de coordenadas polares. La primera coordenada se llama coordenada radial y la segunda coordenada se llama coordenada angular. Cada punto del plano se puede representar de esta forma.
Tenga en cuenta que la ecuación tanθ = y/x tiene un número infinito de soluciones para cualquier par ordenado (x, y). Sin embargo, si restringimos las soluciones a valores entre 0 y 2π, podemos asignar una solución única al cuadrante en el que se encuentra el punto original (x, y). Entonces el valor correspondiente de r es positivo, entonces r² = x² + y².
TEOREMA 8.3.1 Conversión de puntos entre sistemas de coordenadas
Dado un punto P en el plano con coordenadas cartesianas (x, y) y coordenadas polares (r, θ), las siguientes fórmulas de conversión son válidas:
x = rcosθ y y = rsenθ,
r² = x² + y² y tanθ = y/x.
Estas fórmulas se pueden utilizar para convertir de coordenadas rectangulares a polares o de polares a rectangulares. ♦
Ejemplo ilustrativo 8.3_1 Conversión entre coordenadas rectangulares y polares
Convierta cada uno de los siguientes puntos en coordenadas polares.
a. (1, 1)
b. (−3, 4)
c. (0, 3)
d. (5√3, −5)
Convierta cada uno de los siguientes puntos en coordenadas rectangulares.
e. (3, π/3)
f. (2, 3π/2)
g. (6, −5π/6)
Solución:
a. Utilice x = 1 y y = 1 en las ecuaciones r² = x² + y² y tanθ = y/x:
r² = 1² + 1² y tanθ = 1/1 = 1;
r = √2 y θ = π/4
Por lo tanto, este punto se puede representar como (√2, π/4) en coordenadas polares.
b. Utilice x = −3 y y = 4 en las ecuaciones r² = x² + y² y tanθ = y/x:
r² = (−3)² + 4² y tanθ = 4/(−3) = −4/3;
r = 5 y θ = −arctan(4/3) ≈ 2.21
Por lo tanto, este punto se puede representar como (5, 2.21) en coordenadas polares.
c. Utilice x = 0 y y = 3 en las ecuaciones r² = x² + y² y tanθ = y/x:
r² = 0² + 3² y tanθ = 3/0;
r = 3
La aplicación directa de la segunda ecuación conduce a la división por cero. Graficar el punto (0, 3) en el sistema de coordenadas rectangulares revela que el punto está ubicado en el eje y positivo. El ángulo entre el eje x positivo y el eje y positivo es π/2. Por lo tanto, este punto se puede representar como (3, π/2) en coordenadas polares.
d. Utilice x = 5√3 y y = −5 en las ecuaciones r² = x² + y² y tanθ = y/x:
r² = (5√3)² + (−5)² y tanθ = −5/5√3 = −√3/3,
r² = 75 + 25 y θ = arctan(−√3/3);
r = 10 y θ = −π/6.
Por lo tanto, este punto se puede representar como (10, −π/6) en coordenadas polares.
e. Utilice r = 3 y θ = π/3 en las ecuaciones x = rcosθ y y = rsenθ:
x = 3cos(π/3) y y = 3sen(π/3),
x = 3(1/2) = 3/2 y y = 3(√3/2) = 3√3/2
Por lo tanto, este punto se puede representar como (3/2, 3√3/2) en coordenadas rectangulares.
f. Utilice r = 2 y θ = 3π/2 en las ecuaciones x = rcosθ y y = rsenθ:
x = 2cos(3π/2) y y = 2sen(3π/2),
x = 2(0) = 0 y y = 2(−1) = −2
Por lo tanto, este punto se puede representar como (0, −2) en coordenadas rectangulares.
g. Utilice r = 6 y θ = −5π/6 en las ecuaciones x = rcosθ y y = rsenθ:
x = 6cos(−5π/6) y y = 6sen(−5π/6),
x = 6(−√3/2) = −3√3 y y = 6(−1/2) = −3
Por lo tanto, este punto se puede representar como (−3√3, −3) en coordenadas rectangulares. ♦
Ejercicio de control 8.3_1
Convierta (−8, −8) en coordenadas polares y (4, 2π/3) en coordenadas rectangulares. ♦
Representación de un punto en el plano polar
La representación polar de un punto no es única. Por ejemplo, las coordenadas polares (2, π/3) y (2, 7π/3) representan el punto (1, √3) en el sistema rectangular. Además, el valor de r puede ser negativo. Por lo tanto, el punto con coordenadas polares (−2, 4π/3) también representa el punto (1, √3) en el sistema rectangular, como podemos ver usando las ecuaciones x = rcosθ y y = rsenθ:

Cada punto del plano tiene un número infinito de representaciones en coordenadas polares. Sin embargo, cada punto del plano tiene solo una representación en el sistema de coordenadas rectangular.
Tenga en cuenta que la representación polar de un punto en el plano también tiene una interpretación visual. En particular, r es la distancia dirigida a la que se encuentra el punto desde el origen, y θ mide el ángulo que forma el segmento de recta desde el origen hasta un punto con el eje x positivo. Los ángulos positivos se miden en sentido antihorario y los ángulos negativos se miden en sentido horario. El sistema de coordenadas polares aparece en la siguiente figura.

El segmento de recta que comienza en el centro del gráfico y va hacia la derecha (llamado eje x positivo en el sistema cartesiano) es el eje polar. El punto central es el polo u origen del sistema de coordenadas y corresponde a r = 0. El círculo más interno que se muestra en la figura 8.3_2 contiene todos los puntos a una distancia de 1 unidad del polo y está representado por la ecuación r = 1. Entonces r = 2 es el conjunto de puntos a 2 unidades del polo, y así sucesivamente. Los segmentos de recta que emanan del polo corresponden a ángulos fijos. Para trazar un punto en el sistema de coordenadas polares, comience con el ángulo. Si el ángulo es positivo, mida el ángulo desde el eje polar en sentido antihorario. Si es negativo, mídelo en el sentido de las agujas del reloj. Si el valor de r es positivo, mueva esa distancia a lo largo del rayo terminal del ángulo. Si r es negativo, muévase a lo largo del rayo opuesto al rayo terminal del ángulo dado.
Ejemplo ilustrativo 8.3_2 Trazado de puntos en el plano polar
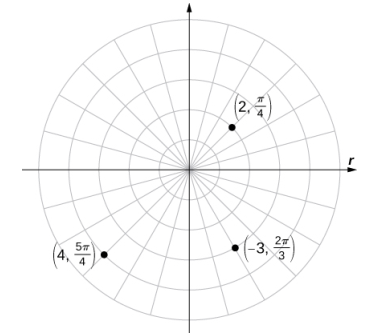
Trace cada uno de los siguientes puntos en el plano polar.
a. (2, π/4)
b. (−3, 2π/3)
c. (4, 5π/4)
Solución:
Los tres puntos se representan en la siguiente figura.
Ejercicio de control 8.3_2
Grafique (4, 5π/3) y (−3, −7π/2) en el plano polar. ♦
Curvas polares
Ahora que sabemos cómo trazar puntos en el sistema de coordenadas polares, podemos analizar cómo trazar curvas. En el sistema de coordenadas rectangulares, podemos graficar una función y = f (x) y crear una curva en el plano cartesiano. De manera similar, podemos graficar una curva que es generada por una función r = f (θ).
La idea general detrás de graficar una función en coordenadas polares es la misma que graficar una función en coordenadas rectangulares. Comience con una lista de valores para la variable independiente (θ en este caso) y calcule los valores correspondientes de la variable dependiente r. Este proceso genera una lista de pares ordenados, que se pueden trazar en el sistema de coordenadas polares. Por último, conecta los puntos y aprovecha los patrones que puedan aparecer. La función puede ser periódica, por ejemplo, lo que indica que solo se necesita un número limitado de valores para la variable independiente.
ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS: TRAZAR UNA CURVA EN COORDENADAS POLARES
| 1. Cree una tabla con dos columnas. La primera columna es para θ y la segunda columna es para r. 2. Cree una lista de valores para θ. 3. Calcule los valores r correspondientes para cada θ. 4. Grafique cada par ordenado (r, θ) en los ejes de coordenadas. 5. Conecta los puntos y busca un patrón. |
Ejemplo ilustrativo 8.3_3 Graficar una función en coordenadas polares
Grafique la curva definida por la función r = 4senθ. Identifica la curva y reescribe la ecuación en coordenadas rectangulares.
Solución:
Debido a que la función es un múltiplo de una función seno, es periódica con un período de 2π, así que use valores para θ entre 0 y 2π. El resultado de los pasos 1 a 3 aparece en la siguiente tabla. La Figura 8.3_4 muestra el gráfico basado en esta tabla.
| θ | r = 4senθ | θ | r = 4senθ | |
|---|---|---|---|---|
| 0 | 0 | π | 0 | |
| π/6 | 2 | 7π/6 | −2 | |
| π/4 | 2√2 ≈ 2.8 | 5π/4 | −2√2 ≈ −2.8 | |
| π/3 | 2√3 ≈ 3.4 | 4π/3 | −2√3 ≈ −3.4 | |
| π/2 | 4 | 3π/2 | −4 | |
| 2π/3 | 2√3 ≈ 3.4 | 5π/3 | 2√3 ≈ −3.4 | |
| 3π/4 | 2√2 ≈ 2.8 | 7π/4 | −2√2 ≈−2.8 | |
| 5π/6 | 2 | 11π/6 | −2 | |
| 2π | 0 |

Esta es la gráfica de una circunferencia. La ecuación r = 4senθ se puede convertir en coordenadas rectangulares multiplicando primero ambos lados por r. Esto da la ecuación r² = 4rsenθ. Luego use los hechos de que r² = x² + y² y y = rsenθ. Esto da x² + y² = 4y. Para poner esta ecuación en forma estándar, reste 4y de ambos lados de la ecuación y complete el cuadrado:
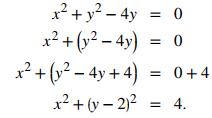
Ésta es la ecuación de una circunferencia con radio 2 y centro (0, 2) en el sistema de coordenadas rectangular.
Ejercicio de control 8.3_3
Cree una gráfica de la curva definida por la función r = 4 + 4cosθ.
La gráfica del ejemplo 8.3_3 era la de una circunferencia. La ecuación de la circunferencia se puede transformar en coordenadas rectangulares usando las fórmulas de transformación de coordenadas en la ecuación r² = x² + y² y tanθ = y/x. El Ejemplo ilustrativo 8.3_5 da algunos ejemplos más de funciones para la transformación de coordenadas polares a rectangulares.
Ejemplo ilustrativo 8.3_4 Transformación de ecuaciones polares en coordenadas rectangulares
Reescribe cada una de las siguientes ecuaciones en coordenadas rectangulares e identifica la gráfica.
a. θ = π/3
b. r = 3
c. r = 6cosθ − 8senθ
Solución:
c. Toma la tangente de ambos lados. Esto da tanθ = tan(π/3) = √3. Dado que tanθ = y/x podemos reemplazar el lado izquierdo de esta ecuación por y/x. Esto da y/x = √3, que se puede reescribir como y = x√3. Ésta es la ecuación de una línea recta que pasa por el origen con pendiente √3. En general, cualquier ecuación polar de la forma θ = K representa una línea recta a través del polo con pendiente igual a tanK.
b. Primero, eleve ambos lados de la ecuación al cuadrado. Esto da r² = 9. Luego reemplace r² con x² + y². Esto da la ecuación x² + y² = 9, que es la ecuación de una circunferencia centrada en el origen con radio 3. En general, cualquier ecuación polar de la forma r = k donde k es una constante positiva representa una circunferencia de radio k centrado Al origen. (Nota: al elevar al cuadrado ambos lados de una ecuación es posible introducir nuevos puntos sin querer. Esto siempre debe tenerse en cuenta. Sin embargo, en este caso no introducimos nuevos puntos. Por ejemplo, (−3, π/3) es el mismo punto que (3, 4π/3).)
c. Multiplica ambos lados de la ecuación por r. Esto conduce a r² = 6rcosθ − 8rsinθ. Luego usa las fórmulas
r² = x² + y², x = rcosθ, y = rsenθ.
Esto da
r² = 6(rcosθ) − 8(rsenθ),
x² + y² = 6x − 8y
Para poner esta ecuación en forma estándar, primero mueva las variables del lado derecho de la ecuación al lado izquierdo, luego complete el cuadrado:
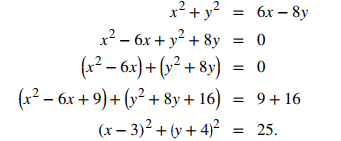
Esta es la ecuación de una circunferencia con centro en (3, −4) y radio 5. Note que la circunferencia pasa por el origen ya que el centro está a 5 unidades de distancia. ♦
Ejercicio de control 8.3_4
Reescriba la ecuación r = secθtanθ en coordenadas rectangulares e identifica su gráfica. ♦
Ya hemos visto varios ejemplos de cómo dibujar gráficas de curvas definidas por ecuaciones polares. En las tablas siguientes se ofrece un resumen de algunas curvas comunes. En cada ecuación, a y b son constantes arbitrarias.
| Nombre | Ecuación | Ejemplo |
| Recta pasando por el polo | θ = k |  |
| Circunferencia | r = acosθ + bsenθ |  |
| Espiral | r = a + bθ |  |
| Cardioide |
r = a(1 + cosθ) r = a(1 − cosθ) r = a(1 + senθ) r = a(1 − senθ) |
 |
| Caracol |
r = acosθ + b r = asenθ + b |
 |
| Rosa |
r = acos(bθ) r = asen(bθ) |
 |
Un cardioide es un caso especial de un caracol, en el que a = b o a = −b. La rosa es una curva muy interesante. Observe que la gráfica de r = 3sen2θ tiene cuatro pétalos. Sin embargo, la gráfica de r = 3sin3θ tiene tres pétalos como se muestra en la siguiente figura.
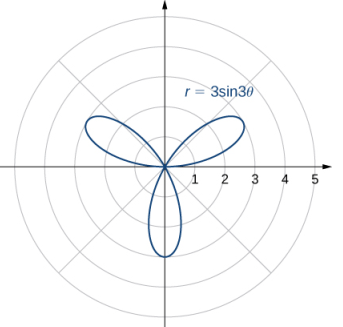
Si el coeficiente de θ es par, el gráfico tiene el doble de pétalos que el coeficiente. Si el coeficiente de θ es impar, entonces el número de pétalos es igual al coeficiente. Se le anima a explorar por qué sucede esto. Surgen gráficos aún más interesantes cuando el coeficiente de θ no es un número entero. Por ejemplo, si es racional, entonces la curva está cerrada; es decir, eventualmente termina donde comenzó (Figura 8.3_6 (a)). Sin embargo, si el coeficiente es irracional, la curva nunca se cierra (Figura 8.3_6 (b)). Aunque puede parecer que la curva está cerrada, un examen más detenido revela que los pétalos justo encima del eje x positivo son ligeramente más gruesos. Esto se debe a que el pétalo no coincide del todo con el punto de partida.


(Figura 8.3_6 Gráficos de rosas polares de funciones con (a) coeficiente racional y (b) coeficiente irracional. Tenga en cuenta que la rosa en la parte (b) en realidad llenaría todo el círculo si se trazara en su totalidad.)
Dado que la curva definida por el gráfico de r = 3sen(πθ) nunca se cierra, la curva representada en la Figura 8.3_6 (b) es solo una representación parcial. De hecho, este es un ejemplo de una curva que llena el espacio. Una curva que llena el espacio es aquella que de hecho ocupa un subconjunto bidimensional del plano real. En este caso, la curva ocupa el círculo de radio 3 centrado en el origen.
Ejemplo ilustrativo 8.3_5 Describiendo una espiral
Recuerde el nautilus en cámara presentado en el inicio del capítulo. Esta criatura muestra una espiral cuando se corta la mitad de la capa exterior. Es posible describir una espiral usando coordenadas rectangulares. La figura 8.3_7 muestra una espiral en coordenadas rectangulares. ¿Cómo describir matemáticamente esta curva?

Suponga que se describe una curva en el sistema de coordenadas polares mediante la función r = f (θ). Dado que tenemos fórmulas de conversión de coordenadas polares a rectangulares dadas por
x = rcosθ
y = rsenθ,
es posible reescribir estas fórmulas usando la función
x = f (θ) cosθ
y = f (θ) senθ.
Este paso proporciona una parametrización de la curva en coordenadas rectangulares utilizando θ como parámetro. Por ejemplo, la fórmula en espiral r = a + bθ se convierte en
x = (a + bθ) cosθ
y = (a + bθ) senθ.
Dejar que θ oscile entre −∞ y ∞ genera la espiral completa.
Simetría en coordenadas polares
Al estudiar la simetría de funciones en coordenadas rectangulares (es decir, en la forma y = f (x)), hablamos de simetría con respecto al eje y y simetría con respecto al origen. En particular, si f (−x) = f (x) para todo x en el dominio de f, entonces f es una función par y su gráfica es simétrica con respecto al eje y. Si f (−x) = −f (x) para todo x en el dominio de f, entonces f es una función impar y su gráfica es simétrica con respecto al origen. Al determinar qué tipos de simetría exhibe una gráfica, podemos aprender más sobre la forma y apariencia de la gráfica. La simetría también puede revelar otras propiedades de la función que genera el gráfico. La simetría en las curvas polares funciona de manera similar.
TEOREMA 7.5 Simetría en ecuaciones y curvas polares
Considere una curva generada por la función r = f (θ) en coordenadas polares.
i. La curva es simétrica con respecto al eje polar si para cada punto (r, θ) en el gráfico, el punto (r, −θ) también está en el gráfico. De manera similar, la ecuación r = f (θ) no cambia al reemplazar θ con −θ.
ii. La curva es simétrica con respecto al polo si para cada punto (r, θ) en el gráfico, el punto (r, π + θ) también está en el gráfico. De manera similar, la ecuación r = f (θ) no cambia cuando se reemplaza r con −r, o θ con π + θ.
iii. La curva es simétrica con respecto a la línea vertical θ = π/2 si para cada punto (r, θ) en el gráfico, el punto (r, π − θ) también está en el gráfico. De manera similar, la ecuación r = f (θ) no cambia cuando θ se reemplaza por π − θ. ♦
La siguiente tabla muestra ejemplos de cada tipo de simetría.
|
Simetría con respecto al eje polar: Para cada punto (r, θ) en la gráfica, también hay un punto reflejado directamente a través del eje horizontal (polar) |
 |
|
Simetría con respecto al polo: Para cada punto (r, θ) en la gráfica, también hay un punto en la gráfica reflejado a través del polo |
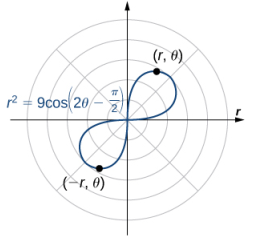 |
|
Simetría con respecto a la recta vertical θ = π/2: Para cada punto (r, θ) en la gráfica, también hay un punto en la gráfica reflejado a través del eje vertical |
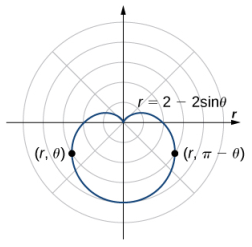 |
Ejemplo ilustrativo 8.3_6 Usar simetría para graficar una ecuación polar
Encuentra la simetría de la rosa definida por la ecuación r = 3sen(2θ) y crea una gráfica.
Solución:
Suponga que el punto (r, θ) está en la gráfica de r = 3sen(2θ).
i. Para probar la simetría con respecto al eje polar, primero intente reemplazar θ con −θ. Esto da r = 3sen(2(−θ)) = −3sen(2θ). Dado que esto cambia la ecuación original, esta prueba no se cumple. Sin embargo, volviendo a la ecuación original y reemplazando r con −r y θ con π − θ se obtiene
−r = 3sen(2(π − θ))
−r = 3sen(2π − 2θ)
−r = 3sen(−2θ)
−r = −3sen2θ.
Multiplicar ambos lados de esta ecuación por −1 da r = 3sen2θ, que es la ecuación original. Esto demuestra que la gráfica es simétrica con respecto al eje polar.
ii. Para probar la simetría con respecto al polo, primero reemplace r con −r, lo que produce −r = 3sen(2θ). Multiplicar ambos lados por −1 da r = −3sen(2θ), que no concuerda con la ecuación original. Por lo tanto, la ecuación no pasa la prueba de esta simetría. Sin embargo, volviendo a la ecuación original y reemplazando θ con θ + π da
r = 3sen(2 (θ + π))
= 3sen(2θ + 2π)
= 3 (sen2θcos2π + cos2θsen2π)
= 3sen2θ.
Dado que esto concuerda con la ecuación original, la gráfica es simétrica con respecto al polo.
iii. Para probar la simetría con respecto a la línea vertical θ = π/2, primero reemplace r con −r y θ con −θ.
−r = 3sen (2(−θ)) − r
= 3sen(−2θ) − r
= −3sen2θ.
Multiplicar ambos lados de esta ecuación por −1 da r = 3sen2θ, que es la ecuación original. Por lo tanto, la gráfica es simétrica con respecto a la línea vertical θ = π/2.
Esta gráfica tiene simetría con respecto al eje polar, el origen y la línea vertical que pasa por el polo. Para graficar la función, tabule los valores de θ entre 0 y π/2 y luego refleje el gráfico resultante.
| θ | r |
|---|---|
| 0 | 0 |
| π/6 | 3√3/2 ≈ 2.6 |
| π/4 | 3 |
| π/3 | 3√3/2 ≈ 2.6 |
| π/2 | 0 |
Esto da un pétalo de rosa, como se muestra en el siguiente gráfico.
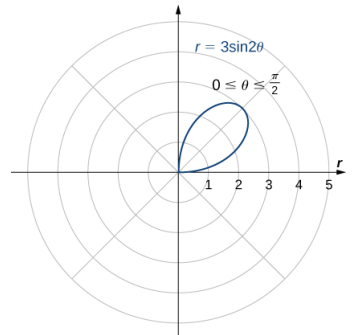
Al reflejar esta imagen en los otros tres cuadrantes se obtiene el gráfico completo como se muestra a continuación:.

Ejercicio de control 8.3_5
Determine la simetría de la gráfica determinada por la ecuación r = 2cos(3θ) y cree una gráfica. ♦

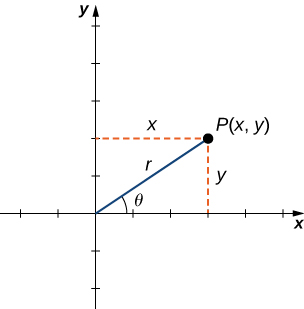
por que en la en la curva polar r=4senθ no se grafica la parte inferio que los angulos son mayores de 180, por ejemplo el punto (-4,3π/2). (-2,7π/6),etc???
¿Cómo luce un ejemplo de una ecuación polar que no es simétrica?
la espiral es una curva no simétrica por ejemplo