| 2. Límites y continuidad | 2.4 continuidad |
Ejercicios propuestos para el Capítulo 2.4
Para los siguientes ejercicios, determina el/los punto(s), si los hay, en los que cada función es discontinua. Clasifica cualquier discontinuidad como de salto, removible, infinita u otra:
- 131. \(f(x) = \frac{1}{\sqrt{x}}\)
- 132. \(f(x) = \frac{2}{x^2 + 1}\)
- 133. \(f(x) = \frac{x}{x^2 – x}\)
- 134. \(g(t) = t^{-1} + 1\)
- 135. \(f(x) = \frac{5}{e^x – 2}\)
- 136. \(f(x) = \frac{|x – 2|}{x – 2}\)
- 137. \(H(x) = \tan 2x\)
- 138. \(f(t) = \frac{t + 3}{t^2 + 5t + 6}\)
Para los siguientes ejercicios, decide si la función es continua en el punto dado. Si es discontinua, ¿qué tipo de discontinuidad es?:
- 139. \(f(x) = \frac{2x^2 – 5x + 3}{x – 1}\) en \(x = 1\)
- 140. \(h(\theta) = \frac{\sin \theta – \cos \theta}{\tan \theta}\) en \(\theta = \pi\)
- 141. \(g(u) = \begin{cases} \frac{6u^2 + u – 2}{2u – 1}, & \text{si } u \ne \frac{1}{2} \\ \frac{7}{2}, & \text{si } u = \frac{1}{2} \end{cases}\) en \(u = \frac{1}{2}\)
- 142. \(f(y) = \frac{\sin(\pi y)}{\tan(\pi y)}\) en \(y = 1\)
- 143. \(f(x) = \begin{cases} x^2 – e^x, & \text{si } x < 0 \\ x - 1, & \text{si } x \ge 0 \end{cases}\) en \(x = 0\)
- 144. \(f(x) = \begin{cases} x \sin(x), & \text{si } x \le \pi \\ x \tan(x), & \text{si } x > \pi \end{cases}\) en \(x = \pi\)
En los siguientes ejercicios, encuentra el/los valor(es) de kk que hacen que cada función sea continua en el intervalo dado:
- 145. \(f(x) = \begin{cases} 3x + 2, & x < k \\ 2x - 3, & k \le x \le 8 \end{cases}\)
- 146. \(f(\theta) = \begin{cases} \sin \theta, & 0 \le \theta < \frac{\pi}{2} \\ \cos(\theta + k), & \frac{\pi}{2} \le \theta \le \pi \end{cases}\)
- 147. \(f(x) = \begin{cases} \frac{x^2 + 3x + 2}{x + 2}, & x \ne -2 \\ k, & x = -2 \end{cases}\)
- 148. \(f(x) = \begin{cases} e^{kx}, & 0 \le x < 4 \\ x + 3, & 4 \le x \le 8 \end{cases}\)
- 149. \(f(x) = \begin{cases} \sqrt{kx}, & 0 \le x \le 3 \\ x + 1, & 3 < x \le 10 \end{cases}\)
En los siguientes ejercicios, usa el Teorema del Valor Intermedio (TVI):
150. Sea \(h(x) = \begin{cases} 3x^2 - 4, & x \le 2 \\ 5 + 4x, & x > 2 \end{cases}\). Sobre el intervalo \([0, 4]\), no hay valor de \(x\) tal que \(h(x) = 10\), aunque \(h(0) < 10\) y \(h(4) > 10\). Explique por qué esto no contradice el TVI.
151. Una partícula que se mueve a lo largo de una línea tiene en cada instante \(t\) una función de posición \(s(t)\), la cual es continua. Asuma que \(s(2) = 5\) y \(s(5) = 2\). Otra partícula se mueve de tal manera que su posición está dada por \(h(t) = s(t) - t\). Explique por qué debe existir un valor \(c\) para \(2 < c < 5\) tal que \(h(c) = 0\).
152. [T] Ten presente la afirmación "El coseno de \(t\) es igual a \(t\) al cubo".
a. Escribe una ecuación matemática de la afirmación.
b. Prueba que la ecuación en la parte a. tiene al menos una solución real.
c. Usa una calculadora para encontrar un intervalo de longitud 0.01 que contenga una solución.
153. Aplica el TVI para determinar si \(2^x = x^3\) tiene una solución en uno de los intervalos [1.25, 1.375] o [1.375, 1.5]. Explica brevemente tu respuesta para cada intervalo.
154. Considera la gráfica de la función \(y = f(x)\) mostrada en la siguiente gráfica.
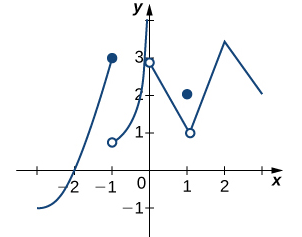
a.Encuentra todos los valores para los cuales la función es discontinua.
b. Para cada valor en la parte a., indica por qué no se aplica la definición formal de continuidad.
c. Clasifica cada discontinuidad como salto, removible o infinita.
155. Sea \(f(x) = \begin{cases} 3x, & x > 1 \\ x^3, & x < 1 \end{cases}\)
a. Dibuja la gráfica de \(f\).
b. ¿Es posible encontrar un valor \(k\) tal que \(f(1) = k\), lo cual hace que \(f(x)\) sea continua para todos los números reales? Explica brevemente.
156. Sea \(f(x) = \frac{x^4 - 1}{x^2 - 1}\) para \(x \ne -1, 1\).
a. Dibuja la gráfica de f.
b. ¿Es posible encontrar valores \(k_1\) y \(k_2\) tales que \(f(-1) = k_1\) y \(f(1) = k_2\), y que hagan que f(x) sea continua para todos los números reales? Explica brevemente.
157. Dibuja la gráfica de la función \(y = f(x)\) con las siguientes propiedades i. a vi.
i. El dominio de \(f\) es \((-\infty, +\infty)\).
ii. \(f\) tiene una discontinuidad infinita en \(x = -6\).
iii. \(f(-6) = 3\)
iv. \(\lim_{x \to -3^-} f(x) = \lim_{x \to -3^+} f(x) = 2\)
v. \(f(-3) = 3\)
vi. \(f\) es continua por la izquierda pero no continua por la derecha en \(x = 3\).
158. Dibuja la gráfica de la función \(y = f(x)\) con las siguientes propiedades i. a iv.
i. El dominio de \(f\) es \([0, 5]\).
ii. \(\lim_{x \to 1^+} f(x)\) y \(\lim_{x \to 1^-} f(x)\) existen y son iguales.
iii. \(f(2)\) es continua por la izquierda pero no continua en \(x = 2\) y continua por la derecha pero no continua en \(x = 3\).
iv. \(f(x)\) tiene una discontinuidad removible en \(x = 1\), una discontinuidad de salto en \(x = 2\), y los siguientes límites se cumplen: \(\lim_{x \to 3^-} f(x) = -\infty\) y \(\lim_{x \to 3^+} f(x) = 2\).
En los siguientes ejercicios, suponga que \(y = f(x)\) está definida para toda \(x\). Para cada descripción, dibuje una gráfica con la propiedad indicada:
159. Discontinua en \(x = 1\) con \(\lim_{x \to 1} f(x) = -1\) y \(\lim_{x \to 2} f(x) = 4\)
160. Discontinua en \(x = 2\) pero continua en cualquier otro punto con \(\lim_{x \to 0} f(x) = \frac{1}{2}\)
Determina si cada una de las afirmaciones dadas es verdadera. Justifica tu respuesta con una explicación o un contraejemplo:
161. \(f(t)=\frac{2}{e^{t}-e^{-t}}\) es continua en todas partes.
162. Si los límites laterales de \(f(x)\) cuando \(x \to a\) existen y son iguales, entonces \(f\) no puede ser discontinua en \(x = a\).
163. Si una función no es continua en un punto, entonces no está definida en ese punto.
164. De acuerdo con el TVI, \(\cos~x-\sin~x-x=2\) tiene una solución en el intervalo [-1,1].
165. Si \(f(x)\) es continua tal que \(f(a)\) y \(f(b)\) tienen signos opuestos, entonces \(f(x)=0\) tiene exactamente una solución en [a, b].
166. La función \(f(x)=\frac{x^{2}-4x+3}{x^{2}-1}\) es continua en el intervalo [0, 3].
167. Si \(f(x)\) es continua en todas partes y \(f(a), f(b) > 0\), entonces no hay una raíz de \(f(x)\) en el intervalo [a, b].
Los siguientes problemas consideran la forma escalar de la ley de Coulomb, la cual describe la fuerza electrostática entre dos cargas puntuales, como electrones. Está dada por la ecuación \(F(r)=k_{e}\frac{|q_{1}q_{2}|}{r^{2}}\) donde \(k_{e}\) es la constante de Coulomb, \(q_{i}\) son las magnitudes de las cargas de las dos partículas, y \(r\) es la distancia entre las dos partículas:
168. Para simplificar el cálculo de un modelo con muchas partículas interactuantes, después de cierto valor umbral \(r = R\), aproximamos \(F\) como cero.
a. Explica el razonamiento físico detrás de esta suposición.
b. ¿Cuál es la ecuación de la fuerza?
c. Evalúa la fuerza \(F\) usando tanto la ley de Coulomb como nuestra aproximación, asumiendo dos protones con una magnitud de carga de \(1.6022 \times 10^{-19}\) culombios (C), y la constante de Coulomb \(k_e = 8.988 \times 10^9 Nm^2/C^2\) están separados por 1 m. Además, asume \(R < 1\) m. ¿Cuánta inexactitud genera nuestra aproximación? ¿Es razonable nuestra aproximación?
d. ¿Existe algún valor finito de \(R\) para el cual este sistema permanezca continuo en \(R\)?
169. En lugar de hacer que la fuerza sea 0 en \(R\), en su lugar, hagamos que la fuerza sea \(10^{-20}\) para \(r \ge R\). Asumiendo dos protones, que tienen una magnitud de carga de \(1.6022 \times 10^{-19} C\), y la constante de Coulomb \(k_e = 8.988 \times 10^9 Nm^2/C^2\). ¿Existe un valor \(R\) que pueda hacer que este sistema sea continuo? Si es así, encuéntralo.
Recordemos la discusión sobre las naves espaciales del inicio del capítulo. Los siguientes problemas consideran el lanzamiento de un cohete desde la superficie de la Tierra. La fuerza de gravedad sobre el cohete está dada por \(F(d) = -mk/d^2\), donde \(m\) es la masa del cohete, \(d\) es la distancia del cohete al centro de la Tierra, y \(k\) es una constante:
170. [T] Determina el valor y las unidades de \(k\) dado que la masa del cohete es de 3 millones de kg. (Pista: La distancia desde el centro de la Tierra a su superficie es de 6378 km).
171. [T] Después de que se ha recorrido cierta distancia \(D\), el efecto gravitacional de la Tierra se vuelve bastante despreciable, por lo que podemos aproximar la función de fuerza por \(F(d) = \begin{cases} -\frac{mk}{d^2} & \text{si } d < D \\ 10,000 & \text{si } d \ge D \end{cases}\). Usando el valor de \(k\) encontrado en el ejercicio anterior, encuentra la condición necesaria \(D\) para que la función de fuerza siga siendo continua.
172. A medida que el cohete se aleja de la superficie de la Tierra, hay una distancia \(D\) donde el cohete se deshace de parte de su masa, ya que ya no necesita el almacenamiento de combustible excedente. Podemos escribir esta función como \(F(d) = \begin{cases} -\frac{m_1 k}{d^2} & \text{si } d < D \\ -\frac{m_2 k}{d^2} & \text{si } d \ge D \end{cases}\). ¿Existe un valor \(D\) tal que esta función sea continua, asumiendo \(m_1 \ne m_2\)?
Demuestra que las siguientes funciones son continuas en todas partes:
173. \(f(\theta) = \sin \theta\)
174. \(g(x) = |x|\)
175. ¿Dónde es continua \(f(x) = \begin{cases} 0 & \text{si } x \text{ es irracional} \\ 1 & \text{si } x \text{ es racional} \end{cases}\)?
