Ejercicios propuestos para el Capítulo 10.12
1. El dominio del campo vectorial F = F(x, y) es un conjunto de puntos (x, y) en un plano, y el rango de F es un conjunto de qué en el plano?
Para los siguientes ejercicios, determine si la afirmación es verdadera o falsa.
-
El campo vectorial $\mathbf{F} = \left\langle 3x^2, 1 \right\rangle$ es un campo gradiente para ambos $\phi_1(x, y) = x^3 + y$ y $\phi_2(x, y) = y + x^3 + 100$.
-
El campo vectorial $\mathbf{F} = \dfrac{\left\langle y, x \right\rangle}{\sqrt{x^2 + y^2}}$ es constante en dirección y magnitud en un círculo unitario.
-
El campo vectorial $\mathbf{F} = \dfrac{\left\langle y, x \right\rangle}{\sqrt{x^2 + y^2}}$ no es ni un campo radial ni una rotación.
Para los siguientes ejercicios, describe cada campo vectorial dibujando algunos de sus vectores.
- [T] F(\(x,y\)) = \( x\mathbf{i} + y\mathbf{j} \)
- [T] F(\(x,y\)) = \( -y\mathbf{i} + x\mathbf{j} \)
- [T] F(\(x,y\)) = \( x\mathbf{i} – y\mathbf{j} \)
- [T] F(\(x,y\)) = \( \mathbf{i} + \mathbf{j} \)
- [T] F(\(x,y\)) = \( 2x\mathbf{i} + 3y\mathbf{j} \)
- [T] F(\(x,y\)) = \( 3\mathbf{i} + x\mathbf{j} \)
- [T] F(\(x,y\)) = \( y\mathbf{i} + \sin(x)\mathbf{j} \)
- [T] F(\(x,y,z\)) = \( x\mathbf{i} + y\mathbf{j} + z\mathbf{k} \)
- [T] F(\(x,y,z\)) = \( 2x\mathbf{i} – 2y\mathbf{j} – 2z\mathbf{k} \)
- [T] F(\(x,y,z\)) = \( \frac{y}{z}\mathbf{i} – \frac{x}{z}\mathbf{j} \)
Para los siguientes ejercicios, encuentra el campo vectorial gradiente de cada función f.
- f(x, y) = \( x \sin(y) + \cos(y) \)
- f(x, y, z) = \( z e^{-xy} \)
- f(x, y, z) = \( x^2 y + xy + y^2 z \)
- f(x, y) = \( x^2 \sin(5y) \)
- f(x, y) = \( \ln(1 + x^2 + 2y^2) \)
- f(x, y, z) = \( x \cos\left(\frac{y}{z}\right) \)
- ¿Cuál es el campo vectorial F(x, y) con un valor en (x, y) que es de longitud unitaria y apunta hacia (1, 0)?
Para los siguientes ejercicios, escribe fórmulas para los campos vectoriales con las propiedades dadas.
- Todos los vectores son paralelos al eje x y todos los vectores en una línea vertical tienen la misma magnitud.
- Todos los vectores apuntan hacia el origen y tienen longitud constante.
- Todos los vectores son de longitud unitaria y son perpendiculares al vector de posición en ese punto.
- Da una fórmula para F(x, y) = M(x, y)\(\mathbf{i}\) + N(x, y)\(\mathbf{j}\) para el campo vectorial en un plano que tiene las propiedades de que F = 0 en (0, 0) y que en cualquier otro punto (a, b), F es tangente al círculo \(x^2 + y^2 = a^2 + b^2\) y apunta en la dirección de las manecillas del reloj con magnitud ||F|| = \(\sqrt{a^2 + b^2}\).
- ¿Es el campo vectorial F(x, y) = (P(x, y), Q(x, y)) = \( (\sin x + y)\mathbf{i} + (\cos y + x)\mathbf{j} \) un campo gradiente?
- Encuentra una fórmula para el campo vectorial F(x, y) = M(x, y)\(\mathbf{i}\) + N(x, y)\(\mathbf{j}\) dado el hecho de que para todos los puntos (x, y), F apunta hacia el origen y ||F|| = \(\frac{10}{x^2 + y^2}\).
Para los siguientes ejercicios, asume que un campo eléctrico en el plano xy causado por una línea infinita de carga a lo largo del eje x es un campo gradiente con función potencial \(V(x, y) = c \ln\left(\frac{r_0}{\sqrt{x^2 + y^2}}\right)\), donde c > 0 es una constante y \(r_0\) es una distancia de referencia en la cual se asume que el potencial es cero.
- Encuentra las componentes del campo eléctrico en las direcciones x e y, donde E(x, y) = \(-\nabla V(x, y)\).
- Muestra que el campo eléctrico en un punto en el plano xy está dirigido hacia afuera desde el origen y tiene magnitud ||E|| = \(\frac{c}{r}\), donde \(r = \sqrt{x^2 + y^2}\).
Una línea de flujo (o línea de corriente) de un campo vectorial F es una curva r(t) tal que dr/dt = F(r(t)). Si F representa el campo de velocidad de una partícula en movimiento, entonces las líneas de flujo son las trayectorias tomadas por la partícula. Por lo tanto, las líneas de flujo son tangentes al campo vectorial. Para los siguientes ejercicios, muestra que la curva dada c(t) es una línea de flujo del campo vectorial de velocidad dado F(x, y, z).
- c(t) = \( \left(e^{2t}, \ln |t|, \frac{1}{t}\right) \), t ≠ 0; F(x, y, z) = \( \left(2x, z, -z^2\right) \)
- c(t) = \( \left(\sin t, \cos t, e^{t}\right) \); F(x, y, z) = \( \left(y, -x, z\right) \)
Para los siguientes ejercicios, sean F = \(x\mathbf{i} + y\mathbf{j}\), G = \(-y\mathbf{i} + x\mathbf{j}\), y H = \(x\mathbf{i} – y\mathbf{j}\). Empareja F, G y H con sus gráficas.
32.
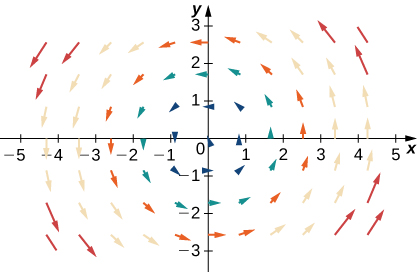
33.
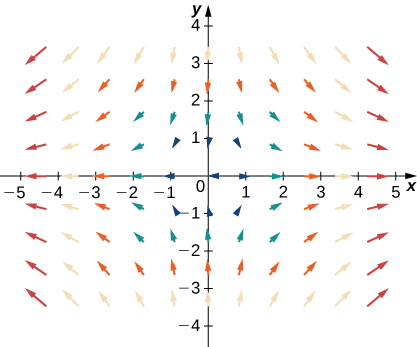
34.
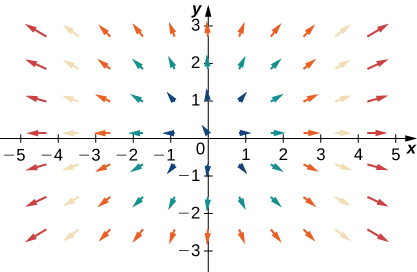
Para los siguientes ejercicios, sean F = \(x\mathbf{i} + y\mathbf{j}\), G = \(-y\mathbf{i} + x\mathbf{j}\), y H = \(x\mathbf{i} – y\mathbf{j}\). Empareja los campos vectoriales con sus gráficas en (1) – (4).
- F + G
- F + H
- G + H
- \(-\)F + G
35.
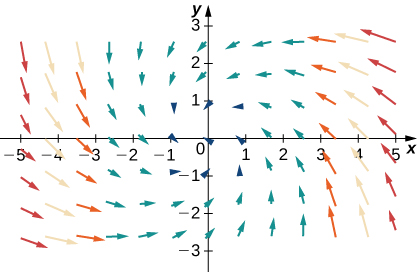
36.
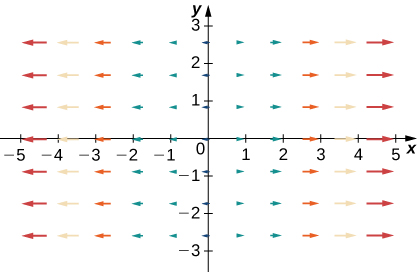
37.
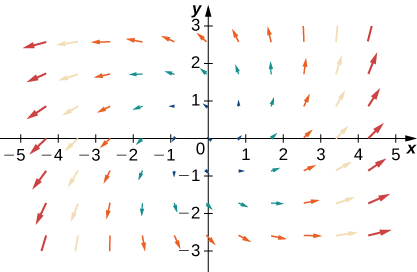
38.
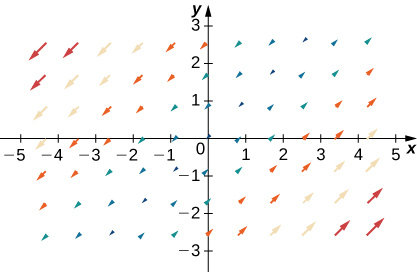

Esto es muy interesante, eres un blogger muy hábil. Me uní a tu feed y espero poder buscar más de tu maravillosa publicación. Además, ¡he compartido su sitio web en mis redes sociales!
Gracias Luis Alberto, provecho!
¿Alguna vez has pensado en publicar un libro electrónico o autor invitado en otros blogs? Tengo un blog basado en la misma información que usted discute y realmente me gustaría que compartiera algunas historias / información. Sé que mis visitantes disfrutarían de tu trabajo. Si está remotamente interesado, no dude en enviarme un correo electrónico.