| 10.9 Calculo de funciones vectoriales |

Ejercicios propuestos para el Capítulo 10.9

Calcula las derivadas de las siguientes funciones vectoriales.

41. \( \mathbf{r}(t) = t^3 \mathbf{i} + 3t^2 \mathbf{j} + \frac{t^3}{6} \mathbf{k} \)
42. \( \mathbf{r}(t) = \sin(t) \mathbf{i} + \cos(t) \mathbf{j} + e^t \mathbf{k} \)
43. \( \mathbf{r}(t) = e^{-t} \mathbf{i} + \sin(3t) \mathbf{j} + 10\sqrt{t} \mathbf{k} \). Aquí se muestra un esbozo de la gráfica. Observa la naturaleza periódica variable de la gráfica.

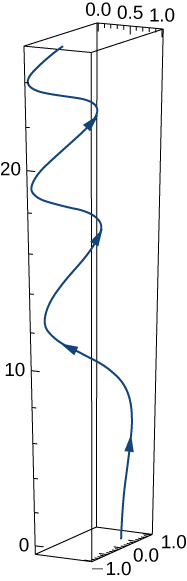
44. \( \mathbf{r}(t) = e^t \mathbf{i} + 2e^t \mathbf{j} + \mathbf{k} \)
45. \( \mathbf{r}(t) = \mathbf{i} + \mathbf{j} + \mathbf{k} \)
46. \( \mathbf{r}(t) = te^t \mathbf{i} + t\ln(t) \mathbf{j} + \sin(3t) \mathbf{k} \)
47. \( \mathbf{r}(t) = \frac{1}{t+1} \mathbf{i} + \arctan(t) \mathbf{j} + \ln t^3 \mathbf{k} \)
48. \( \mathbf{r}(t) = \tan(2t) \mathbf{i} + \sec(2t) \mathbf{j} + \sin^2(t) \mathbf{k} \)
49. \( \mathbf{r}(t) = 3\mathbf{i} + 4\sin(3t) \mathbf{j} + t\cos(t) \mathbf{k} \)
50. \( \mathbf{r}(t) = t^2 \mathbf{i} + te^{-2t} \mathbf{j} – 5e^{-4t} \mathbf{k} \)

Para los siguientes problemas, encuentra un vector tangente en el valor indicado de t.

51. \( \mathbf{r}(t) = t \mathbf{i} + \sin(2t) \mathbf{j} + \cos(3t) \mathbf{k}; t = \frac{\pi}{3} \)
52. \( \mathbf{r}(t) = 3t^3 \mathbf{i} + 2t^2 \mathbf{j} + \frac{1}{t} \mathbf{k}; t = 1 \)
53. \( \mathbf{r}(t) = 3e^t \mathbf{i} + 2e^{-3t} \mathbf{j} + 4e^{2t} \mathbf{k}; t = \ln(2) \)
54. \( \mathbf{r}(t) = \cos(2t) \mathbf{i} + 2\sin t \mathbf{j} + t^2 \mathbf{k}; t = \frac{\pi}{2} \)

Encuentra el vector tangente unitario para las siguientes curvas parametrizadas.

55. \( \mathbf{r}(t) = 6\mathbf{i} + \cos(3t)\mathbf{j} + 3\sin(4t)\mathbf{k}, 0 \leq t < 2\pi \). Aquí se presentan dos vistas de esta curva:

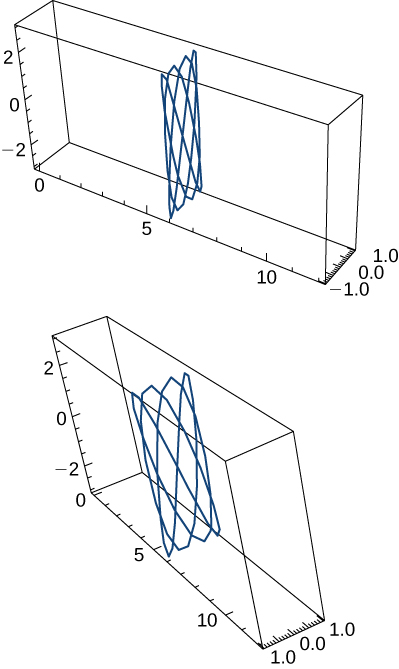
56. \( \mathbf{r}(t) = \cos t \mathbf{i} + \sin t \mathbf{j} + \sin t \mathbf{k}, 0 \leq t < 2\pi. \)
57. \( \mathbf{r}(t) = 3\cos(4t) \mathbf{i} + 3\sin(4t) \mathbf{j} + 5t \mathbf{k}, 1 \leq t \leq 2 \)
58. \( \mathbf{r}(t) = t \mathbf{i} + 3t \mathbf{j} + t^2 \mathbf{k} \)

Sean \( \mathbf{r}(t) = t \mathbf{i} + t^2 \mathbf{j} – t^4 \mathbf{k} \) y \( \mathbf{s}(t) = \sin(t) \mathbf{i} + e^t \mathbf{j} + \cos(t) \mathbf{k} \). Aquí está la gráfica de la función:

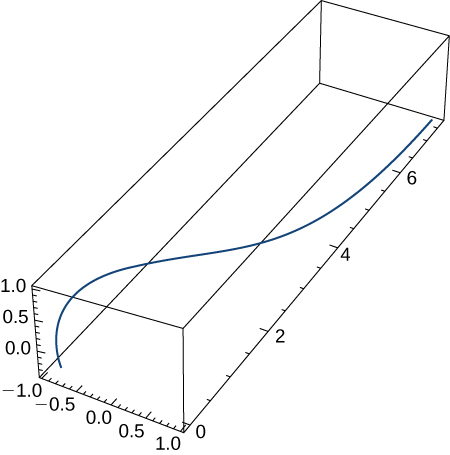
Encuentra lo siguiente:

59. \( \frac{d}{dt} [\mathbf{r}(t^2)] \)
60. \( \frac{d}{dt} [t^2 \cdot \mathbf{s}(t)] \)
61. \( \frac{d}{dt} [\mathbf{r}(t) \cdot \mathbf{s}(t)] \)
62. Calcula la primera, segunda y tercera derivada de \( \mathbf{r}(t) = 3t \mathbf{i} + 6\ln(t) \mathbf{j} + 5e^{-3t} \mathbf{k} \).
63. Encuentra \( \mathbf{r}'(t) \cdot \mathbf{r}”(t) \) para \( \mathbf{r}(t) = -3t^5 \mathbf{i} + 5t \mathbf{j} + 2t^2 \mathbf{k} \).
64. La función de aceleración, la velocidad inicial y la posición inicial de una partícula son \( \mathbf{a}(t) = -5\cos t \mathbf{i} – 5\sin t \mathbf{j} \), \( \mathbf{v}(0) = 9\mathbf{i} + 2\mathbf{j} \) y \( \mathbf{r}(0) = 5\mathbf{i} \). Encuentra \( \mathbf{v}(t) \) y \( \mathbf{r}(t) \).
65. El vector posición de una partícula es \( \mathbf{r}(t) = 5\sec(2t) \mathbf{i} – 4\tan(t) \mathbf{j} + 7t^2 \mathbf{k} \).
    1. Grafica la función posición y muestra una vista de la gráfica que ilustre el comportamiento asintótico de la función.
    2. Encuentra la velocidad cuando t se aproxima a, pero no es igual a, \( \pi/4 \) (si existe).
66. Encuentra la velocidad y la rapidez de una partícula con la función posición \( \mathbf{r}(t) = \left(\frac{2t-1}{2t+1}\right) \mathbf{i} + \ln(1 – 4t^2) \mathbf{j} \). La rapidez de una partícula es la magnitud de la velocidad y se representa por \( \|\mathbf{r}'(t)\| \).

Una partícula se mueve en una trayectoria circular de radio b de acuerdo con la función \( \mathbf{r}(t) = b\cos(\omega t) \mathbf{i} + b\sin(\omega t) \mathbf{j} \), donde \( \omega \) es la velocidad angular, \( d\theta/dt \).

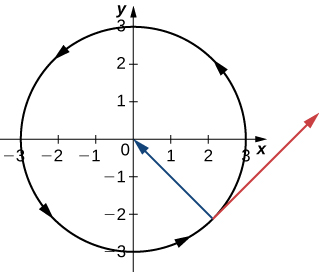
67. Encuentra la función de velocidad y muestra que \( \mathbf{v}(t) \) es siempre ortogonal a \( \mathbf{r}(t) \).
68. Muestra que la rapidez de la partícula es proporcional a la velocidad angular.
69. Evalúa \( \frac{d}{dt} [\mathbf{u}(t) \times \mathbf{u}'(t)] \) dado \( \mathbf{u}(t) = t^2 \mathbf{i} – 2t \mathbf{j} + \mathbf{k} \).
70. Encuentra la antiderivada de \( \mathbf{r}'(t) = \cos(2t) \mathbf{i} – 2\sin t \mathbf{j} + \frac{1}{1+t^2} \mathbf{k} \) que satisface la condición inicial \( \mathbf{r}(0) = 3\mathbf{i} – 2\mathbf{j} + \mathbf{k} \).
71. Evalúa \( \int_0^3 \|\mathbf{t} \mathbf{i} + t^2 \mathbf{j}\| \, dt \).
72. Un objeto parte del reposo en el punto \( P(1, 2, 0) \) y se mueve con una aceleración de \( \mathbf{a}(t) = \mathbf{j} + 2\mathbf{k} \), donde \( \|\mathbf{a}(t)\| \) se mide en pies por segundo al cuadrado. Encuentra la ubicación del objeto después de \( t = 2 \) segundos.
73. Muestra que si la rapidez de una partícula que viaja a lo largo de una curva representada por una función vectorial es constante, entonces la función de velocidad es siempre perpendicular a la función de aceleración.
74. Dado \( \mathbf{r}(t) = t \mathbf{i} + 3t \mathbf{j} + t^2 \mathbf{k} \) y \( \mathbf{u}(t) = 4t \mathbf{i} + t^2 \mathbf{j} + t^3 \mathbf{k} \), encuentra \( \frac{d}{dt} (\mathbf{r}(t) \times \mathbf{u}(t)) \).
75. Dado \( \mathbf{r}(t) = (t + \cos t, t – \sin t) \), encuentra la velocidad y la rapidez en cualquier momento t.
76. Encuentra el vector velocidad para la función \( \mathbf{r}(t) = \langle e^t, e^{-t}, 0 \rangle \).
77. Encuentra la ecuación de la recta tangente a la curva \( \mathbf{r}(t) = \langle e^t, e^{-t}, 0 \rangle \) en \( t = 0 \).
78. Describe y esboza la curva representada por la función vectorial \( \mathbf{r}(t) = \langle 6t, 6t – t^2 \rangle \).
79. Localiza el punto más alto en la curva \( \mathbf{r}(t) = \langle 6t, 6t – t^2 \rangle \) y da el valor de la función en este punto.

El vector posición para una partícula es \( \mathbf{r}(t) = t\mathbf{i} + t^2\mathbf{j} + t^3\mathbf{k} \). La gráfica se muestra aquí:

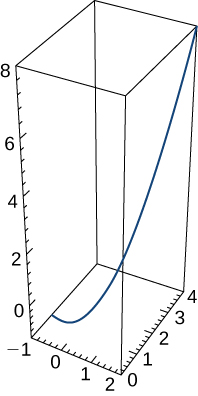
80. Encuentra el vector velocidad en cualquier momento t.
81. Encuentra la rapidez de la partícula en el tiempo \( t = 2 \) segundos.
82. Encuentra la aceleración en el tiempo \( t = 2 \) segundos.

Una partícula viaja a lo largo del camino de una hélice con la ecuación \( \mathbf{r}(t) = \cos(t) \mathbf{i} + \sin(t) \mathbf{j} + t \mathbf{k} \). Ve la gráfica presentada aquí:

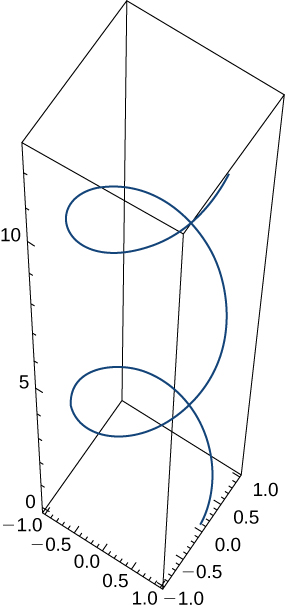
Encuentra lo siguiente:

83. Velocidad de la partícula en cualquier momento t.
84. Rapidez de la partícula en cualquier momento t.
85. Aceleración de la partícula en cualquier momento t.
86. Encuentra el vector tangente unitario para la hélice.

Una partícula viaja a lo largo del camino de una elipse con la ecuación \( \mathbf{r}(t) = \cos t \mathbf{i} + 2\sin t \mathbf{j} + 0 \mathbf{k} \). Encuentra lo siguiente:

87. Velocidad de la partícula.
88. Rapidez de la partícula en \( t = \frac{\pi}{4} \).
89. Aceleración de la partícula en \( t = \frac{\pi}{4} \).

Dada la función vectorial \( \mathbf{r}(t) = \langle \tan t, \sec t, 0 \rangle \) (la gráfica se muestra aquí), encuentra lo siguiente:

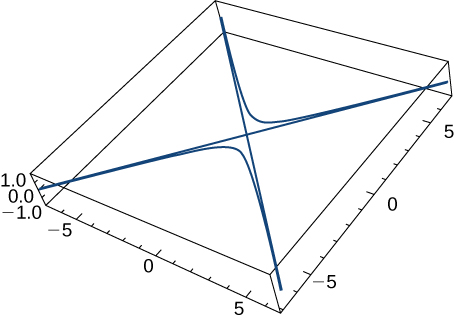
90. Velocidad
91. Rapidez
92. Aceleración
93. Encuentra la rapidez mínima de una partícula viajando a lo largo de la curva \( \mathbf{r}(t) = \langle t + \cos t, t – \sin t \rangle, t \in [0, 2\pi] \).

Dado \( \mathbf{r}(t) = t \mathbf{i} + 2\sin t \mathbf{j} + 2\cos t \mathbf{k} \) y \( \mathbf{u}(t) = \frac{1}{t} \mathbf{i} + 2\sin t \mathbf{j} + 2\cos t \mathbf{k} \), encuentra lo siguiente:

94. \( \mathbf{r}(t) \times \mathbf{u}(t) \)
95. \( \frac{d}{dt} (\mathbf{r}(t) \times \mathbf{u}(t)) \)
96. Ahora, usa la regla del producto para la derivada del producto cruz de dos vectores y muestra que este resultado es el mismo que la respuesta para el problema anterior.

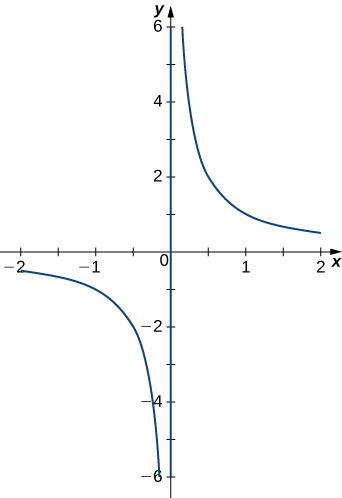
Encuentra el vector tangente unitario \( \mathbf{T}(t) \) para la siguiente función vectorial:

97. \( \mathbf{r}(t) = \left\langle t, \frac{1}{t} \right\rangle \). La gráfica se muestra aquí:

98. \( \mathbf{r}(t) = \langle t \cos t, t \sin t \rangle \)
99. \( \mathbf{r}(t) = \langle t + 1, 2t + 1, 2t + 2 \rangle \)

Evalúa las siguientes integrales:

100. \( \displaystyle \int \left(e^t \mathbf{i} + \sin t \mathbf{j} + \frac{1}{2t-1} \mathbf{k} \right) dt \)
101. \( \displaystyle \int_0^1 \mathbf{r}(t) dt \), donde \( \mathbf{r}(t) = \left\langle \sqrt[3]{t}, \frac{1}{t+1}, e^{-t} \right\rangle \)