Por /

Álgebra lineal con aplicaciones

| 2. Álgebra de matrices | Ejercicios propuestos para el Capítulo 2.3 |

2.3 Multiplicación matricial

En la Sección 2.2 se introdujeron los productos matriz-vector. Si $\mathit{A}$ es una matriz de $m \times n$, el producto $\mathit{A}\mathbf{x}$ se definió para cualquier vector columna de $n$ componentes $\mathbf{x}$ en $\mathbb{R}^n$ de la siguiente manera: Si

$$ \mathit{A} = \begin{bmatrix} \mathbf{a}_1 & \mathbf{a}_2 & \cdots & \mathbf{a}_n \end{bmatrix} $$

donde los $\mathbf{a}_j$ son las columnas de $\mathit{A}$, y si

$$ \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \text{, la Definición 2.5 dice} $$
$$ \mathit{A}\mathbf{x} = x_1\mathbf{a}_1 + x_2\mathbf{a}_2 + \cdots + x_n\mathbf{a}_n \quad \mathbf{(2.5)} $$

Esto fue motivado como una forma de describir sistemas de ecuaciones lineales con matriz de coeficientes $\mathit{A}$. De hecho, cada sistema de este tipo tiene la forma $\mathit{A}\mathbf{x} = \mathbf{b}$ donde $\mathbf{b}$ es el vector columna de constantes.

Nota: Ver la Definición 2.5 

En esta sección extendemos la multiplicación matriz-vector a una forma de multiplicar matrices en general, y luego investigamos el álgebra matricial por sí misma. Aunque comparte varias propiedades de la aritmética ordinaria, pronto quedará claro que la aritmética matricial es diferente en varios aspectos. La multiplicación de matrices está estrechamente relacionada con la composición de transformaciones.

Composición y multiplicación de matrices

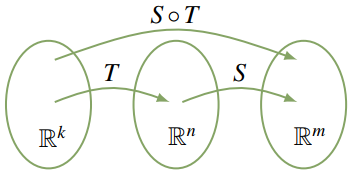
A veces, dos transformaciones se “encadenan” de la siguiente manera:

$$ \mathbb{R}^k \xrightarrow{T} \mathbb{R}^n \xrightarrow{S} \mathbb{R}^m $$

En este caso, podemos aplicar $T$ primero y luego aplicar $S$, y el resultado es una nueva transformación

$$ S \circ T : \mathbb{R}^k \to \mathbb{R}^m $$

llamada la compuesta de $S$ y $T$, definida por

$$ (S \circ T)(\mathbf{x}) = S[T(\mathbf{x})] \quad \text{para todo } \mathbf{x} \text{ en } \mathbb{R}^k $$

La acción de $S \circ T$ se puede describir como “primero $T$ y luego $S$” (¡nótese el orden!). Esta nueva transformación se describe en el diagrama. El lector habrá encontrado la composición de funciones ordinarias: por ejemplo, considere $\mathbb{R} \xrightarrow{g} \mathbb{R} \xrightarrow{f} \mathbb{R}$ donde $f(x) = x^2$ y $g(x) = x+1$ para todo $x$ en $\mathbb{R}$. Entonces

$$ (f \circ g)(x) = f[g(x)] = f(x+1) = (x+1)^2 $$

y

$$ (g \circ f)(x) = g[f(x)] = g(x^2) = x^2 + 1 $$

para todo $x$ en $\mathbb{R}$.

Nuestra preocupación aquí son las transformaciones matriciales. Suponga que $\mathbf{A}$ es una matriz de $m \times n$ y $\mathbf{B}$ es una matriz de $n \times k$, y sea $\mathbb{R}^k \xrightarrow{T_\mathbf{B}} \mathbb{R}^n \xrightarrow{T_\mathbf{A}} \mathbb{R}^m$ las transformaciones matriciales inducidas por $\mathbf{B}$ y $\mathbf{A}$ respectivamente, es decir:

$$ T_{\mathbf{B}}(\mathbf{x}) = \mathbf{B}\mathbf{x} \text{ para todo } \mathbf{x} \text{ en } \mathbb{R}^k \quad \text{y} \quad T_{\mathbf{A}}(\mathbf{y}) = \mathbf{A}\mathbf{y} \text{ para todo } \mathbf{y} \text{ en } \mathbb{R}^n $$

Escriba $\mathbf{B} = \begin{bmatrix} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_k \end{bmatrix}$ donde $\mathbf{b}_j$ denota la columna $j$ de $\mathbf{B}$ para cada $j$. Por lo tanto, cada $\mathbf{b}_j$ es un $n$-vector ($\mathbf{B}$ es $n \times k$) de modo que podemos formar el producto matriz-vector $\mathbf{A}\mathbf{b}_j$. En particular, obtenemos una matriz de $m \times k$

$$ \begin{bmatrix} \mathbf{A}\mathbf{b}_1 & \mathbf{A}\mathbf{b}_2 & \cdots & \mathbf{A}\mathbf{b}_k \end{bmatrix} $$

con columnas $\mathbf{A}\mathbf{b}_1, \mathbf{A}\mathbf{b}_2, \ldots, \mathbf{A}\mathbf{b}_k$. Ahora, calcule $(T_{\mathbf{A}} \circ T_{\mathbf{B}})(\mathbf{x})$ para cualquier

$$ \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_k \end{bmatrix} \text{ en } \mathbb{R}^k\text{:} $$ $$ \begin{aligned} (T_{\mathbf{A}} \circ T_{\mathbf{B}})(\mathbf{x}) &= T_{\mathbf{A}}[T_{\mathbf{B}}(\mathbf{x})] && \text{Definición de } T_{\mathbf{A}} \circ T_{\mathbf{B}} \\ &= \mathbf{A}(\mathbf{B}\mathbf{x}) \\ &= \mathbf{A}(x_1\mathbf{b}_1 + x_2\mathbf{b}_2 + \cdots + x_k\mathbf{b}_k) && \text{Ecuación 2.5 anterior} \\ &= \mathbf{A}(x_1\mathbf{b}_1) + \mathbf{A}(x_2\mathbf{b}_2) + \cdots + \mathbf{A}(x_k\mathbf{b}_k) && \text{Teorema 2.2.2} \\ &= x_1(\mathbf{A}\mathbf{b}_1) + x_2(\mathbf{A}\mathbf{b}_2) + \cdots + x_k(\mathbf{A}\mathbf{b}_k) && \text{Teorema 2.2.2} \\ &= \begin{bmatrix} \mathbf{A}\mathbf{b}_1 & \mathbf{A}\mathbf{b}_2 & \cdots & \mathbf{A}\mathbf{b}_k \end{bmatrix} \mathbf{x} && \text{Ecuación 2.5 anterior} \end{aligned} $$

Debido a que $\mathbf{x}$ era un vector arbitrario en $\mathbb{R}^n$, esto muestra que $T_{\mathbf{A}} \circ T_{\mathbf{B}}$ es la transformación matricial inducida por la matriz $\begin{bmatrix} \mathbf{A}\mathbf{b}_1 & \mathbf{A}\mathbf{b}_2 & \cdots & \mathbf{A}\mathbf{b}_n \end{bmatrix}$. Esto motiva la siguiente definición.

Nota: Ver el Teorema 2.2.2

Definición 2.9 Multiplicación de Matrices

Sea $\mathbf{A}$ una matriz de $m \times n$, sea $\mathbf{B}$ una matriz de $n \times k$, y escriba $B = [ \mathbf{b}_1 \ \mathbf{b}_2 \ \cdots \ \mathbf{b}_k ]$, donde $\mathbf{b}_j$ es la columna $j$ de $B$ para cada $j$. La matriz producto $\mathbf{AB}$ es la matriz de $m \times k$ definida de la siguiente manera:

$$AB = A [ \mathbf{b}_1 \ \mathbf{b}_2 \ \cdots \ \mathbf{b}_k ] = [ A\mathbf{b}_1 \ A\mathbf{b}_2 \ \cdots \ A\mathbf{b}_k ]$$

Por lo tanto, la matriz producto $AB$ se da en términos de sus columnas $\mathbf{Ab}_1$, $\mathbf{Ab}_2$, …, $\mathbf{Ab}_n$. La columna $j$ de $AB$ es el producto matriz-vector $\mathbf{Ab}_j$ de $A$ y la columna correspondiente $\mathbf{b}_j$ de $B$. Observe que dicho producto $\mathbf{Ab}_j$ tiene sentido por la Definición 2.5 porque $A$ es de $m \times n$ y cada $\mathbf{b}_j$ está en $\mathbb{R}^n$ (ya que $B$ tiene $n$ filas). Note también que si $B$ es una matriz columna, esta definición se reduce a la Definición 2.5 para la multiplicación matriz-vector.

Dadas las matrices $A$ y $B$, la Definición 2.9 y la computación anterior dan

$$A(B\mathbf{x}) = [ \mathbf{Ab}_1 \ \mathbf{Ab}_2 \ \cdots \ \mathbf{Ab}_n ] \mathbf{x} = (AB)\mathbf{x}$$

para todo $\mathbf{x}$ en $\mathbb{R}^k$. Registramos esto como referencia.

Teorema 2.3.1

Sea $A$ una matriz de $m \times n$ y sea $B$ una matriz de $n \times k$. Entonces la matriz producto $AB$ es de $m \times k$ y satisface

$$A(B\mathbf{x}) = (AB)\mathbf{x} \quad \text{para todo } \mathbf{x} \text{ en } \mathbb{R}^k$$

He aquí un ejemplo de cómo calcular el producto AB de dos matrices utilizando la Definición 2.9.

Ejemplo 2.3.1

Calcule $AB$ si $A = \begin{bmatrix} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{bmatrix}$ y $B = \begin{bmatrix} 8 & 9 \\ 7 & 2 \\ 6 & 1 \end{bmatrix}$.

Solución. Las columnas de $B$ son $\mathbf{b}_1 = \begin{bmatrix} 8 \\ 7 \\ 6 \end{bmatrix}$ y $\mathbf{b}_2 = \begin{bmatrix} 9 \\ 2 \\ 1 \end{bmatrix}$, por lo que la Definición 2.5 da

$$\mathbf{Ab}_1 = \begin{bmatrix} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{bmatrix} \begin{bmatrix} 8 \\ 7 \\ 6 \end{bmatrix} = \begin{bmatrix} 67 \\ 78 \\ 55 \end{bmatrix} \quad \text{y} \quad \mathbf{Ab}_2 = \begin{bmatrix} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{bmatrix} \begin{bmatrix} 9 \\ 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 29 \\ 24 \\ 10 \end{bmatrix}$$

Por lo tanto, la Definición 2.9 anterior da $AB = [ \mathbf{Ab}_1 \ \mathbf{Ab}_2 ] = \begin{bmatrix} 67 & 29 \\ 78 & 24 \\ 55 & 10 \end{bmatrix}$.

Ejemplo 2.3.2

Si $A$ es $m \times n$ y $B$ es $n \times k$, el Teorema 2.3.1 proporciona una fórmula simple para la composición de las transformaciones matriciales $T_A$ y $T_B$:

$$T_A \circ T_B = T_{AB}$$

Solución. Dado cualquier $\mathbf{x}$ en $\mathbb{R}^k$,

$$ \begin{aligned} (T_A \circ T_B)(\mathbf{x}) &= T_A[T_B(\mathbf{x})] \\ &= A[B\mathbf{x}] \\ &= (AB)\mathbf{x} \\ &= T_{AB}(\mathbf{x}) \end{aligned} $$

      Si bien la Definición 2.9 es importante, existe otra manera de calcular el producto de matrices AB que permite determinar cada entrada individual. En la Sección 2.2 definimos el producto punto de dos n‑tuplas como la suma de los productos de las entradas correspondientes. Luego mostramos (Teorema 2.2.5) que si A es una matriz m × n y x es un vector de dimensión n, entonces la entrada j del producto Ax es el producto punto de la fila j de A con x. Esta observación fue llamada la ″regla del producto punto″ para la multiplicación matriz‑vector, y el siguiente teorema muestra que se extiende a la multiplicación de matrices en general.

Teorema 2.3.2: Regla del Producto Punto

Sean $A$ y $B$ matrices de tamaños $m \times n$ y $n \times k$, respectivamente. Entonces, la entrada $(i, j)$ de $AB$ es el producto punto de la fila $i$ de $A$ con la columna $j$ de $B$.

Prueba. Escriba $B = [ \mathbf{b}_1 \ \mathbf{b}_2 \ \cdots \ \mathbf{b}_n ]$ en términos de sus columnas. Entonces $\mathbf{Ab}_j$ es la columna $j$ de $AB$ para cada $j$. Por lo tanto, la entrada $(i, j)$ de $AB$ es la entrada $i$ de $\mathbf{Ab}_j$, que es el producto punto de la fila $i$ de $A$ con $\mathbf{b}_j$. Esto prueba el teorema. $\square$

Así, para calcular la entrada (i, j) de AB, proceda de la siguiente manera (véase el diagrama): Recorra la fila i de A y la columna j de B, multiplique las entradas correspondientes y sume los resultados.

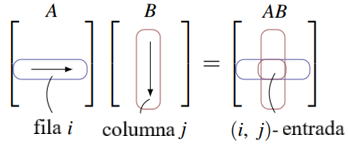
Nótese que esto requiere que las filas de A tengan la misma longitud que las columnas de B. La siguiente regla es útil para recordar este hecho y para determinar el tamaño de la matriz producto AB.

Regla de compatibilidad

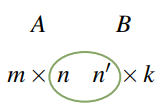
Sean A y B matrices. Si A es de tamaño m × n y B es de tamaño n′ × k, el producto AB puede formarse si y solo si n = n′. En este caso, el tamaño de la matriz producto AB es m × k, y decimos que AB está definido, o que A y B son compatibles para la multiplicación.

El diagrama proporciona una regla mnemotécnica útil para recordar esto. Adoptamos la siguiente convención:

Convención

Siempre que se escribe un producto de matrices, se asume tácitamente que los tamaños de los factores son tales que el producto está definido. ♦

Para ilustrar la regla del producto punto, recalculamos el producto de matrices en el Ejemplo 2.3.1.

Ejemplo 2.3.3

Calcule $AB$ si $A = \begin{bmatrix} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{bmatrix}$ y $B = \begin{bmatrix} 8 & 9 \\ 7 & 2 \\ 6 & 1 \end{bmatrix}$.

Solución. Aquí $A$ es de $3 \times 3$ y $B$ es de $3 \times 2$, por lo que la matriz producto $AB$ está definida y será de tamaño $3 \times 2$. El Teorema 2.3.2 da cada entrada de $AB$ como el producto punto de la fila correspondiente de $A$ con la columna correspondiente de $B$, es decir,

$$AB = \begin{bmatrix} 2 & 3 & 5 \\ 1 & 4 & 7 \\ 0 & 1 & 8 \end{bmatrix} \begin{bmatrix} 8 & 9 \\ 7 & 2 \\ 6 & 1 \end{bmatrix} = \begin{bmatrix} 2 \cdot 8 + 3 \cdot 7 + 5 \cdot 6 & 2 \cdot 9 + 3 \cdot 2 + 5 \cdot 1 \\ 1 \cdot 8 + 4 \cdot 7 + 7 \cdot 6 & 1 \cdot 9 + 4 \cdot 2 + 7 \cdot 1 \\ 0 \cdot 8 + 1 \cdot 7 + 8 \cdot 6 & 0 \cdot 9 + 1 \cdot 2 + 8 \cdot 1 \end{bmatrix} = \begin{bmatrix} 67 & 29 \\ 78 & 24 \\ 55 & 10 \end{bmatrix}$$

De curso, esto concuerda con el Ejemplo 2.3.1.

Ejemplo 2.3.4

Calcule las entradas $(1, 3)$ y $(2, 4)$ de $AB$ donde

$$A = \begin{bmatrix} 3 & -1 & 2 \\ 0 & 1 & 4 \end{bmatrix} \quad \text{y} \quad B = \begin{bmatrix} 2 & 1 & 6 & 0 \\ 0 & 2 & 3 & 4 \\ -1 & 0 & 5 & 8 \end{bmatrix}$$

Luego calcule $AB$.

Solución. La entrada $(1, 3)$ de $AB$ es el producto punto de la fila 1 de $A$ y la columna 3 de $B$ (resaltada en la siguiente visualización), calculada multiplicando las entradas correspondientes y sumando los resultados.

$$\begin{bmatrix} 3 & -1 & 2 \\ 0 & 1 & 4 \end{bmatrix} \begin{bmatrix} 2 & 1 & \mathbf{6} & 0 \\ 0 & 2 & \mathbf{3} & 4 \\ -1 & 0 & \mathbf{5} & 8 \end{bmatrix} \quad (1, 3)\text{-entrada} = 3 \cdot 6 + (-1) \cdot 3 + 2 \cdot 5 = 25$$

De manera similar, la entrada $(2, 4)$ de $AB$ involucra la fila 2 de $A$ y la columna 4 de $B$.

$$\begin{bmatrix} 3 & -1 & 2 \\ \mathbf{0} & \mathbf{1} & \mathbf{4} \end{bmatrix} \begin{bmatrix} 2 & 1 & 6 & \mathbf{0} \\ 0 & 2 & 3 & \mathbf{4} \\ -1 & 0 & 5 & \mathbf{8} \end{bmatrix} \quad (2, 4)\text{-entrada} = 0 \cdot 0 + 1 \cdot 4 + 4 \cdot 8 = 36$$

Dado que $A$ es de $2 \times 3$ y $B$ es de $3 \times 4$, el producto es de $2 \times 4$.

$$AB = \begin{bmatrix} 3 & -1 & 2 \\ 0 & 1 & 4 \end{bmatrix} \begin{bmatrix} 2 & 1 & 6 & 0 \\ 0 & 2 & 3 & 4 \\ -1 & 0 & 5 & 8 \end{bmatrix} = \begin{bmatrix} 4 & 1 & 25 & 12 \\ -4 & 2 & 23 & 36 \end{bmatrix}$$

Ejemplo 2.3.5

Si $A = \begin{bmatrix} 1 & 3 & 2 \end{bmatrix}$ y $B = \begin{bmatrix} 5 \\ 6 \\ 4 \end{bmatrix}$, calcule $A^2$, $AB$, $BA$, y $B^2$ cuando estén definidos.

Solución. Aquí, $A$ es una matriz de $1 \times 3$ y $B$ es una matriz de $3 \times 1$, por lo que $A^2$ y $B^2$ no están definidos. Sin embargo, la regla de compatibilidad establece:

A    B
$1 \times 3$ y $3 \times 1$
B    A
$3 \times 1$ y $1 \times 3$

así, tanto $AB$ como $BA$ pueden formarse y son matrices de $1 \times 1$ y $3 \times 3$, respectivamente.

$$AB = \begin{bmatrix} 1 & 3 & 2 \end{bmatrix} \begin{bmatrix} 5 \\ 6 \\ 4 \end{bmatrix} = [ 1 \cdot 5 + 3 \cdot 6 + 2 \cdot 4 ] = [ 31 ]$$
$$BA = \begin{bmatrix} 5 \\ 6 \\ 4 \end{bmatrix} \begin{bmatrix} 1 & 3 & 2 \end{bmatrix} = \begin{bmatrix} 5 \cdot 1 & 5 \cdot 3 & 5 \cdot 2 \\ 6 \cdot 1 & 6 \cdot 3 & 6 \cdot 2 \\ 4 \cdot 1 & 4 \cdot 3 & 4 \cdot 2 \end{bmatrix} = \begin{bmatrix} 5 & 15 & 10 \\ 6 & 18 & 12 \\ 4 & 12 & 8 \end{bmatrix}$$

Nota: En cuanto a los números, escribimos A2 = A·A, A3 = A·A·A, etc. Nótese que A2 está definido si y solo si A tiene tamaño n × n para algún n.

      A diferencia de la multiplicación numérica, los productos de matrices AB y BA no necesitan ser iguales. De hecho, ni siquiera necesitan tener el mismo tamaño, como muestra el Ejemplo 2.3.5. Resulta poco común que AB = BA (aunque no es imposible), y se dice que A y B conmutan cuando esto ocurre.

Ejemplo 2.3.6

Sea $A = \begin{bmatrix} 6 & 9 \\ -4 & -6 \end{bmatrix}$ y $B = \begin{bmatrix} 1 & 2 \\ -1 & 0 \end{bmatrix}$. Calcule $A^2$, $AB$, $BA$.

Solución. $$A^2 = \begin{bmatrix} 6 & 9 \\ -4 & -6 \end{bmatrix} \begin{bmatrix} 6 & 9 \\ -4 & -6 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$$ por lo que $A^2 = 0$ puede ocurrir incluso si $A \ne 0$. A continuación,

$$AB = \begin{bmatrix} 6 & 9 \\ -4 & -6 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ -1 & 0 \end{bmatrix} = \begin{bmatrix} -3 & 12 \\ 2 & -8 \end{bmatrix}$$
$$BA = \begin{bmatrix} 1 & 2 \\ -1 & 0 \end{bmatrix} \begin{bmatrix} 6 & 9 \\ -4 & -6 \end{bmatrix} = \begin{bmatrix} -2 & -3 \\ -6 & -9 \end{bmatrix}$$

Por lo tanto, $AB \ne BA$, a pesar de que $AB$ y $BA$ son del mismo tamaño.

Ejemplo 2.3.7

Si $A$ es cualquier matriz, entonces $IA = A$ y $AI = A$, donde $I$ denota una matriz identidad de un tamaño tal que las multiplicaciones están definidas.

Solución. Ambos casos se derivan de la regla del producto punto, como el lector debe verificar. Para una prueba más formal, escriba $A = [ \mathbf{a}_1 \ \mathbf{a}_2 \ \cdots \ \mathbf{a}_n ]$ donde $\mathbf{a}_j$ es la columna $j$ de $A$. Entonces la Definición 2.9 y el Ejemplo 2.2.11 dan:

$$IA = [ I\mathbf{a}_1 \ I\mathbf{a}_2 \ \cdots \ I\mathbf{a}_n ] = [ \mathbf{a}_1 \ \mathbf{a}_2 \ \cdots \ \mathbf{a}_n ] = A$$

Si $\mathbf{e}_j$ denota la columna $j$ de $I$, entonces $A\mathbf{e}_j = \mathbf{a}_j$ para cada $j$ por el Ejemplo 2.2.12. Por lo tanto, la Definición 2.9 da:

$$AI = A [ \mathbf{e}_1 \ \mathbf{e}_2 \ \cdots \ \mathbf{e}_n ] = [ A\mathbf{e}_1 \ A\mathbf{e}_2 \ \cdots \ A\mathbf{e}_n ] = [ \mathbf{a}_1 \ \mathbf{a}_2 \ \cdots \ \mathbf{a}_n ] = A$$

      El siguiente teorema recopila varios resultados sobre la multiplicación de matrices que se utilizan en todas partes en álgebra lineal.

Teorema 2.3.3

Asuma que $a$ es cualquier escalar, y que $A$, $B$ y $C$ son matrices de tamaños tales que los productos matriciales indicados están definidos. Entonces:

  1. $IA = A$ y $AI = A$ donde $I$ denota una matriz identidad.
  2. $A(BC) = (AB)C$.
  3. $A(B + C) = AB + AC$.
  1. $(B + C)A = BA + CA$.
  2. $a(AB) = (aA)B = A(aB)$.
  3. $(AB)^T = B^T A^T$.

Prueba. La condición (1) es el Ejemplo 2.3.7; probamos (2), (4) y (6) y dejamos (3) y (5) como ejercicios.

2. Si $C = [ \mathbf{c}_1 \ \mathbf{c}_2 \ \cdots \ \mathbf{c}_k ]$ en términos de sus columnas, entonces $BC = [ B\mathbf{c}_1 \ B\mathbf{c}_2 \ \cdots \ B\mathbf{c}_k ]$ por la Definición 2.9, por lo que

$$ \begin{aligned} A(BC) &= [ A(B\mathbf{c}_1) \ A(B\mathbf{c}_2) \ \cdots \ A(B\mathbf{c}_k) ] \quad \text{Definición 2.9} \\ &= [ (AB)\mathbf{c}_1 \ (AB)\mathbf{c}_2 \ \cdots \ (AB)\mathbf{c}_k ] \quad \text{Teorema 2.3.1} \\ &= (AB)C \quad \text{Definición 2.9} \end{aligned} $$

4. Sabemos (Teorema 2.2.2) que $(B+C)\mathbf{x} = B\mathbf{x} + C\mathbf{x}$ se cumple para cada vector columna $\mathbf{x}$. Si escribimos $A = [ \mathbf{a}_1 \ \mathbf{a}_2 \ \cdots \ \mathbf{a}_n ]$ en términos de sus columnas, obtenemos

$$ \begin{aligned} (B+C)A &= [ (B+C)\mathbf{a}_1 \ (B+C)\mathbf{a}_2 \ \cdots \ (B+C)\mathbf{a}_n ] \quad \text{Definición 2.9} \\ &= [ B\mathbf{a}_1 + C\mathbf{a}_1 \ B\mathbf{a}_2 + C\mathbf{a}_2 \ \cdots \ B\mathbf{a}_n + C\mathbf{a}_n ] \quad \text{Teorema 2.2.2} \\ &= [ B\mathbf{a}_1 \ B\mathbf{a}_2 \ \cdots \ B\mathbf{a}_n ] + [ C\mathbf{a}_1 \ C\mathbf{a}_2 \ \cdots \ C\mathbf{a}_n ] \quad \text{Adición de Columnas} \\ &= BA + CA \quad \text{Definición 2.9} \end{aligned} $$

6. Como en la Sección 2.1 , escriba $A = [a_{ij}]$ y $B = [b_{ij}]$, de modo que $A^T = [a’_{ij}]$ y $B^T = [b’_{ij}]$ donde $a’_{ij} = a_{ji}$ y $b’_{ij} = b_{ji}$. Si $c_{ij}$ denota la entrada $(i, j)$ de $B^T A^T$, entonces $c_{ij}$ es el producto punto de la fila $i$ de $B^T$ con la columna $j$ de $A^T$. Por lo tanto,

$$ \begin{aligned} c_{ij} &= b’_{i1}a’_{1j} + b’_{i2}a’_{2j} + \cdots + b’_{im}a’_{mj} \\ &= b_{1i}a_{j1} + b_{2i}a_{j2} + \cdots + b_{mi}a_{jm} \\ &= a_{j1}b_{1i} + a_{j2}b_{2i} + \cdots + a_{jm}b_{mi} \end{aligned} $$

Pero este es el producto punto de la fila $j$ de $A$ con la columna $i$ de $B$; es decir, la entrada $(j, i)$ de $(AB)^T$. Esto prueba (6). $\square$

Nota: Acceder fácilmente al Teorema 2.3.1

      La propiedad 2 en el Teorema 2.3.3 se llama la ley asociativa de la multiplicación de matrices. Afirma que la ecuación A(BC) = (AB)C se cumple para todas las matrices (si los productos están definidos). Por lo tanto, este producto es el mismo sin importar cómo se forme, y por eso se escribe simplemente como ABC. Esto se extiende: El producto ABCD de Se pueden formar cuatro matrices de varias maneras, por ejemplo, (AB)(CD), [A(BC)]D y A[B(CD)], pero la ley asociativa implica que todas son iguales y, por lo tanto, se escriben como ABCD. Una observación similar se aplica en general: los productos de matrices pueden escribirse de manera inequívoca sin paréntesis.

       Sin embargo, debe tomarse una nota de precaución sobre la multiplicación de matrices: el hecho de que AB y BA no necesariamente sean iguales significa que el orden de los factores es importante en un producto de matrices. Por ejemplo, ABCD y ADCB pueden no ser iguales.

Advertencia: Si se cambia el orden de los factores en un producto de matrices, la matriz resultante puede cambiar (o puede no estar definida). ¡Ignorar esta advertencia es una fuente de muchos errores entre los estudiantes de álgebra lineal!

       Las propiedades 3 y 4 en el Teorema 2.3.3 se denominan leyes distributivas. Afirman que A(B + C)  =  AB + AC y (B + C)A = BA + CA se cumplen siempre que las sumas y productos estén definidos. Estas reglas se extienden a más de dos términos y, junto con la Propiedad 5, aseguran que muchas manipulaciones familiares del álgebra ordinaria se extiendan a las matrices. Por ejemplo,

A(2B − 3C + D − 5E) = 2AB − 3AC + AD − 5AE

(A + 3C − 2D)B = AB + 3CB − 2DB

Note nuevamente que la advertencia sigue en vigor: por ejemplo, A(B − C) no necesariamente es igual a AB − CA. Estas reglas permiten simplificar muchas expresiones matriciales.

Ejemplo 2.3.8

Simplifique la expresión $A(BC – CD) + A(C – B)D – AB(C – D)$.

Solución.

$$ \begin{aligned} A(BC – CD) + A(C – B)D – AB(C – D) &= A(BC) – A(CD) + (AC – AB)D – (AB)C + (AB)D \\ &= ABC – ACD + ACD – ABD – ABC + ABD \\ &= 0 \end{aligned} $$

      El Ejemplo 2.3.9 y el Ejemplo 2.3.10 a continuación muestran cómo podemos usar las propiedades del Teorema 2.3.2 para deducir otros hechos sobre la multiplicación de matrices. Se dice que las matrices A y B conmutan si AB = BA.

Ejemplo 2.3.9

Suponga que $A$, $B$ y $C$ son matrices de $n \times n$ y que tanto $A$ como $B$ conmutan con $C$; es decir, $AC = CA$ y $BC = CB$. Muestre que $AB$ conmuta con $C$.

Solución. Mostrar que $AB$ conmuta con $C$ significa verificar que $(AB)C = C(AB)$. La computación utiliza la ley asociativa varias veces, así como los hechos dados de que $AC = CA$ y $BC = CB$.

$$(AB)C = A(BC) = A(CB) = (AC)B = (CA)B = C(AB)$$

Ejemplo 2.3.10

Muestre que $AB = BA$ si y solo si $(A – B)(A + B) = A^2 – B^2$.

Solución. Lo siguiente siempre se cumple:

$$(A – B)(A + B) = A(A + B) – B(A + B) = A^2 + AB – BA – B^2 \quad (2.6)$$

Por lo tanto, si $AB = BA$, entonces $(A – B)(A + B) = A^2 – B^2$ se cumple. Inversamente, si esta última ecuación se cumple, entonces la Ecuación (2.6) se convierte en

$$A^2 – B^2 = A^2 + AB – BA – B^2$$

Esto da $0 = AB – BA$, y $AB = BA$ se cumple.

      En la Sección 2.2 vimos (en el Teorema 2.2.1) que todo sistema de ecuaciones lineales tiene la forma

Ax = b,

donde A es la matriz de coeficientes, x es la columna de variables y b es la matriz de constantes. Así, el sistema de ecuaciones lineales se convierte en una única ecuación matricial. La multiplicación de matrices puede proporcionar información sobre dicho sistema.

Ejemplo 2.3.11

Considere un sistema $A\mathbf{x} = \mathbf{b}$ de ecuaciones lineales donde $A$ es una matriz de $m \times n$. Asuma que existe una matriz $C$ tal que $CA = I_n$. Si el sistema $A\mathbf{x} = \mathbf{b}$ tiene una solución, muestre que esta solución debe ser $C\mathbf{b}$. Dé una condición que garantice que $C\mathbf{b}$ es, de hecho, una solución.

Solución. Suponga que $\mathbf{x}$ es cualquier solución del sistema, de modo que $A\mathbf{x} = \mathbf{b}$. Multiplique ambos lados de esta ecuación matricial por $C$ para obtener, sucesivamente:

$$C(A\mathbf{x}) = C\mathbf{b}, \quad (CA)\mathbf{x} = C\mathbf{b}, \quad I_n\mathbf{x} = C\mathbf{b}, \quad \mathbf{x} = C\mathbf{b}$$

Esto muestra que si el sistema tiene una solución $\mathbf{x}$, entonces esa solución debe ser $\mathbf{x} = C\mathbf{b}$, como se requiere. Pero esto no garantiza que el sistema tenga una solución. Sin embargo, si escribimos $\mathbf{x}_1 = C\mathbf{b}$, entonces

$$A\mathbf{x}_1 = A(C\mathbf{b}) = (AC)\mathbf{b}$$

Así $\mathbf{x}_1 = C\mathbf{b}$ será una solución si la condición $AC = I_m$ es satisfecha.

      Las ideas del Ejemplo 2.3.11 llevan a información importante sobre matrices; esto se abordará en la siguiente sección.

Multiplicación por bloques

Definición 2.10 Partición en Bloques de una Matriz

A menudo es útil considerar matrices cuyas entradas son ellas mismas matrices (llamadas bloques). Una matriz vista de esta manera se dice que está particionada en bloques.

Por ejemplo, escribir una matriz $B$ en la forma $B = [ \mathbf{b}_1 \ \mathbf{b}_2 \ \cdots \ \mathbf{b}_k ]$ donde $\mathbf{b}_j$ son las columnas de $B$ es una partición en bloques de $B$. Aquí hay otro ejemplo. Considere las matrices

$$A = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 2 & -1 & 4 & 2 & 1 \\ 3 & 1 & -1 & 7 & 5 \end{bmatrix} = \begin{bmatrix} I_2 & 0_{23} \\ P & Q \end{bmatrix} \quad \text{y} \quad B = \begin{bmatrix} 4 & -2 \\ 5 & 6 \\ 7 & 3 \\ 0 & 1 \\ -1 & 6 \end{bmatrix} = \begin{bmatrix} X \\ Y \end{bmatrix}$$

donde los bloques han sido etiquetados como se indica. Esta es una forma natural de particionar $A$ en bloques debido a los bloques $I_2$ y $0_{23}$ que ocurren. Esta notación es particularmente útil cuando multiplicamos las matrices $A$ y $B$ porque el producto $AB$ puede calcularse en forma de bloques como sigue:

$$AB = \begin{bmatrix} I & 0 \\ P & Q \end{bmatrix} \begin{bmatrix} X \\ Y \end{bmatrix} = \begin{bmatrix} IX + 0Y \\ PX + QY \end{bmatrix} = \begin{bmatrix} X \\ PX + QY \end{bmatrix} = \begin{bmatrix} 4 & -2 \\ 5 & 6 \\ 30 & 8 \\ 8 & 27 \end{bmatrix}$$

Esto se puede comprobar fácilmente que es el producto AB, calculado de la manera convencional.

       En otras palabras, podemos calcular el producto AB mediante la multiplicación ordinaria de matrices, usando bloques como entradas. El único requisito es que los bloques sean compatibles. Es decir, los tamaños de los bloques deben ser tales que todos los productos (de matrices) de bloques que se presenten tengan sentido. Esto significa que el número de columnas en cada bloque de A debe ser igual al número de filas en el bloque correspondiente de B.

Teorema 2.3.4: Multiplicación de Bloques

Si las matrices $A$ y $B$ están particionadas compatiblemente en bloques, el producto $AB$ se puede calcular mediante la multiplicación matricial usando bloques como entradas.

Omitimos la prueba del anterior Teorema.

Hemos estado utilizando dos casos de multiplicación por bloques. Si $B = \begin{bmatrix} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_k \end{bmatrix}$ es una matriz donde las $\mathbf{b}_j$ son las columnas de $B$, y si el producto matricial $AB$ está definido, entonces tenemos

$$AB = A \begin{bmatrix} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_k \end{bmatrix} = \begin{bmatrix} A\mathbf{b}_1 & A\mathbf{b}_2 & \cdots & A\mathbf{b}_k \end{bmatrix}$$

Esta es la Definición 2.9 y es una multiplicación en bloque donde A = [A] tiene solo un bloque. Como otra ilustración,

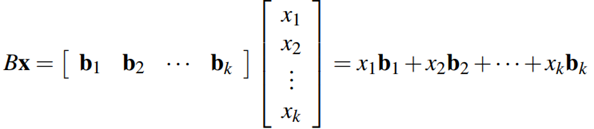
dónde x es cualquier matriz columna de k × 1 (esta es la Definición 2.5).

      No es nuestra intención abordar la multiplicación de bloques en detalle aquí. Sin embargo, damos un ejemplo adicional porque se utilizará más adelante.

Teorema 2.3.5

Suponga que las matrices $A = \begin{bmatrix} B & X \\ 0 & C \end{bmatrix}$ y $A_1 = \begin{bmatrix} B_1 & X_1 \\ 0 & C_1 \end{bmatrix}$ están particionadas como se muestra, donde $B$ y $B_1$ son matrices cuadradas del mismo tamaño, y $C$ y $C_1$ también son cuadradas del mismo tamaño. Estas son particiones compatibles y la multiplicación por bloques resulta en:

$$AA_1 = \begin{bmatrix} B & X \\ 0 & C \end{bmatrix} \begin{bmatrix} B_1 & X_1 \\ 0 & C_1 \end{bmatrix} = \begin{bmatrix} BB_1 & BX_1 + XC_1 \\ 0 & CC_1 \end{bmatrix}$$

Ejemplo 2.3.12

Obtenga una fórmula para $A^k$ donde $A = \begin{bmatrix} I & X \\ 0 & I \end{bmatrix}$ es cuadrada e $I$ es una matriz identidad.

Solución. Tenemos que

$$A^2 = \begin{bmatrix} I & X \\ 0 & I \end{bmatrix} \begin{bmatrix} I & X \\ 0 & I \end{bmatrix} = \begin{bmatrix} I^2+X0 & IX+XI \\ 0I+I0 & 0X+I^2 \end{bmatrix} = \begin{bmatrix} I & 2X \\ 0 & I \end{bmatrix}$$

Luego:

$$A^3 = A A^2 = \begin{bmatrix} I & X \\ 0 & I \end{bmatrix} \begin{bmatrix} I & 2X \\ 0 & I \end{bmatrix} = \begin{bmatrix} I & 3X \\ 0 & I \end{bmatrix}$$

Continuando de esta manera, vemos que $A^k = \begin{bmatrix} I & kX \\ 0 & I \end{bmatrix}$ para cada $k \geq 1$.

      La multiplicación por bloques tiene usos teóricos, como veremos. Sin embargo, también es útil para calcular productos de matrices en una computadora con capacidad de memoria limitada. Las matrices se dividen en bloques de tal manera que cada producto de bloques se pueda manejar. Luego, los bloques se almacenan en memoria auxiliar y sus productos se calculan uno por uno.

Grafos Dirigidos

El estudio de los grafos dirigidos ilustra cómo la multiplicación de matrices surge de maneras distintas al estudio de ecuaciones lineales o transformaciones de matrices.

Un grafo dirigido consiste en un conjunto de puntos (llamados vértices) conectados por flechas (llamadas aristas). Por ejemplo, los vértices podrían representar ciudades y las aristas, vuelos disponibles. Si el grafo tiene $n$ vértices $v_1, v_2, \ldots, v_n$, la matriz de adyacencia $A = [a_{ij}]$ es la matriz de $n \times n$ cuya entrada $(i, j)$, $a_{ij}$, es $1$ si existe una arista desde $v_j$ a $v_i$ (observe el orden), y cero en caso contrario. Por ejemplo, la matriz de adyacencia del grafo dirigido que se muestra es

$$A = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}.$$

Un camino de longitud $r$ (o un $r$-camino) desde el vértice $j$ al vértice $i$ es una secuencia de $r$ aristas que conducen de $v_j$ a $v_i$. Por lo tanto, $v_1 \to v_2 \to v_1 \to v_1 \to v_3$ es un 4-camino de $v_1$ a $v_3$ en el grafo dado. Las aristas son simplemente los caminos de longitud 1, por lo que la entrada $(i, j)$, $a_{ij}$, de la matriz de adyacencia $A$ es el número de 1-caminos de $v_j$ a $v_i$. Esta observación tiene una extensión importante:

Teorema 2.3.6

Si $A$ es la matriz de adyacencia de un grafo dirigido con $n$ vértices, entonces la entrada $(i, j)$ de $A^r$ es el número de $r$-caminos $v_j \to v_i$.

Como ilustración, considere la matriz de adyacencia $A$ en el grafo mostrado. Entonces $$ A = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}, \quad A^2 = \begin{bmatrix} 2 & 1 & 1 \\ 2 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix}, \quad \text{y} \quad A^3 = \begin{bmatrix} 4 & 2 & 1 \\ 3 & 2 & 1 \\ 2 & 1 & 1 \end{bmatrix} $$ Por lo tanto, dado que la entrada $(2, 1)$-ésima de $A^2$ es $2$, existen dos $2$-caminos $v_1 \to v_2$ (de hecho, son $v_1 \to v_2 \to v_2$ y $v_1 \to v_3 \to v_2$). De manera similar, la entrada $(2, 3)$-ésima de $A^2$ es cero, por lo que no hay $2$-caminos $v_3 \to v_2$, como el lector puede verificar. El hecho de que ninguna entrada de $A^3$ sea cero muestra que es posible ir de cualquier vértice a cualquier otro en exactamente tres pasos. Para ver por qué el Teorema 2.3.6 es verdadero, observe que este afirma que $$ \text{la entrada }(i, j)\text{-ésima de } A^r \text{ es igual al número de } r\text{-caminos } v_j \to v_i \tag{2.7} $$ para cada $r \ge 1$. Procedemos por inducción sobre $r$ (ver Apéndice C). El caso $r=1$ es la definición de la matriz de adyacencia. Asumimos inductivamente que (2.7) es verdadera para algún $r \ge 1$; debemos probar que (2.7) también es válida para $r+1$. Pero cada $(r+1)$-camino $v_j \to v_i$ es el resultado de un $r$-camino $v_j \to v_k$ para algún $k$, seguido de un $1$-camino $v_k \to v_i$. Escribiendo $A = [a_{ij}]$ y $A^r = [b_{ij}]$, hay $b_{kj}$ caminos del primer tipo (por inducción) y $a_{ik}$ caminos del segundo tipo, y sumando sobre $k$, esto muestra que hay $$ a_{i1}b_{1j} + a_{i2}b_{2j} + \dots + a_{in}b_{nj} \text{ } (r+1)\text{-caminos } v_j \to v_i $$ Pero esta suma es el producto escalar de la $i$-ésima fila $[a_{i1} \text{ } a_{i2} \text{ } \dots \text{ } a_{in}]$ de $A$ con la $j$-ésima columna $[b_{1j} \text{ } b_{2j} \text{ } \dots \text{ } b_{nj}]^T$ de $A^r$. Como tal, es la entrada $(i, j)$ de la matriz producto $A A^r = A^{r+1}$. Esto demuestra que (2.7) es válida para $r+1$, como se requiere.
Páginas: 1 2