| 9. Ecuaciones diferenciales | Ejercicios propuestos del Capítulo 9.7.1 |

9.7. Soluciones en serie de ecuaciones lineales de segundo orden

      EN ESTE CAPÍTULO estudiamos una clase de ecuaciones diferenciales de segundo orden que ocurren en muchas aplicaciones, pero que no se pueden resolver en forma cerrada en términos de funciones elementales. Aquí hay unos ejemplos:

(1) Ecuación de Bessel

x²y′′ + xy′ + (x² − ν²)y = 0,

que ocurre en problemas que muestran simetría cilíndrica, como la difracción de la luz a través de una abertura circular, la propagación de la radiación electromagnética a través de un cable coaxial y las vibraciones de un parche de tambor circular.

(2) Ecuación de Airy

y′′ − xy = 0,

que ocurre en la astronomía y la física cuántica.

(3) Ecuación de Legendre

(1 − x²)y′′ − 2xy′ + α(α + 1)y = 0,

que ocurre en problemas que muestran simetría esférica, particularmente en electromagnetismo.

        Las anteriores ecuaciones y otras consideradas en este capítulo se pueden escribir en la forma

P₀(x)y′′ + P₁(x)y′ + P₂(x)y = 0,        (A)

donde P₀, P₁ y P₂ son polinomios sin factor común. Para la mayoría de las ecuaciones que ocurren en las aplicaciones, estos polinomios son de grado dos o menor. Impondremos esta restricción, aunque los métodos que desarrollaremos se pueden extender al caso en que las funciones de los coeficientes sean polinomios de grado arbitrario, o incluso series de potencias que convergen en algún círculo alrededor del origen en el plano complejo.

      Dado que (A) en general no tiene soluciones de forma cerrada, buscamos representaciones en serie para las soluciones. Veremos que si P₀(0) ≠ 0 entonces las soluciones de (A) se pueden escribir como series de potencias

que convergen en un intervalo abierto centrado en x = 0.

LA SECCIÓN 9.7.1 revisa las propiedades de las series de potencias.

LAS SECCIONES 9.7.2 y 9.7.3 están dedicadas a encontrar soluciones en serie de potencias de (A) en el caso donde P₀(0) ≠ 0. La situación es más complicada si P₀(0) = 0; sin embargo, si P₁ y P₂ satisfacen los supuestos que se aplican a la mayoría de las ecuaciones de interés, entonces podemos usar un método de series modificadas para obtener soluciones de (A).

La SECCIÓN 9.7.4 introduce los supuestos apropiados sobre P₁ y P₂ en el caso en que P₀(0) = 0, y trata la ecuación de Euler

ax²y′′ + bxy′ + cy = 0,

donde a, b y c son constantes. Esta es la ecuación más simple que satisface estos supuestos.

Las SECCIONES: Sección 9.7.5, Sección 9.7.6 y Sección 9.7.7 tratan de tres casos distintos que satisfacen los supuestos introducidos en la Sección 9.7.4. En los tres casos, (A) tiene al menos una solución de la forma

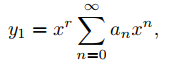
donde r no necesita ser un número entero. El problema es que hay tres posibilidades, cada una de las cuales requiere un enfoque diferente, para la forma de una segunda solución y₂ tal que {y₁, y₂} sea un par fundamental de soluciones de (A).

9.7.1 REVISIÓN DE SERIES DE POTENCIAS

       Muchas aplicaciones dan lugar a ecuaciones diferenciales con soluciones que no se pueden expresar en términos de funciones elementales como polinomios, funciones racionales, funciones exponenciales y logarítmicas y funciones trigonométricas. Las soluciones de algunas de las más importantes de estas ecuaciones se pueden expresar en términos de series de potencias. Estudiaremos tales ecuaciones en este capítulo. En esta sección revisamos las propiedades relevantes de las series de potencias. Omitiremos las pruebas, que se pueden encontrar aquí en Cálculo21.

Definición 9.7.1.1: Serie de potencias en x − x₀

Una serie infinita de la forma

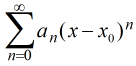,       (9.7.1.1)

donde x₀ y a₀, a₁, . . . , a_n, . . . son constantes, se llama serie de potencias en x − x₀. Decimos que la serie de potencias (9.7.1.1) converge para una x dada si el límite

existe; de lo contrario, decimos que la serie de potencias diverge para la x dada.  ♦

      Una serie de potencias en x − x₀ debe converger si x = x₀, ya que las potencias positivas de x − x₀ son todas cero en este caso. Este puede ser el único valor de x para el que converge la serie de potencias. Sin embargo, el siguiente teorema muestra que si la serie de potencias converge para alguna x ≠ x₀ entonces el conjunto de todos los valores de x para los cuales converge forma un intervalo.

Teorema 9.7.1.1: Convergencia y divergencia de una serie de potencias

Para cualquier serie de potencias

,

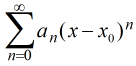exactamente una de las siguientes afirmaciones es verdadera:

(i) La serie de potencias converge solo para x = x₀.

(ii) La serie de potencias converge para todos los valores de x.

(iii) Existe un número positivo R tal que la serie de potencias converge si |x − x₀| < R y diverge si |x − x₀| > R.  ♦

      En el caso (iii) decimos que R es el radio de convergencia de la serie de potencias. Por conveniencia, incluimos los otros dos casos en esta definición tomando R = 0 en el caso (i) y R = ∞ en el caso (ii). Definimos el intervalo abierto de convergencia de 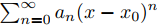como

(x₀ − R, x₀ + R)   si   0 < R < ∞,   o   (−∞, ∞) si R = ∞.

Si R es finito, no se puede hacer ninguna afirmación general sobre la convergencia en los extremos x = x₀ ± R del intervalo abierto de convergencia; la serie puede converger en uno o ambos puntos, o divergir en ambos.

      Recuerde del cálculo que una serie de constantes 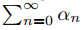se dice que converge absolutamente si la serie de valores absolutos 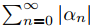converge. Se puede demostrar que una serie de potencias 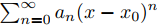con un radio de convergencia positivo R converge absolutamente en su intervalo abierto de convergencia; es decir, la serie

de valores absolutos converge si |x − x₀| < R. Sin embargo, si R < ∞, la serie puede no converger absolutamente en un extremo x₀ ± R, incluso si converge allí.

      El siguiente teorema proporciona un método útil para determinar el radio de convergencia de una serie de potencias. Se obtiene en cálculo aplicando la prueba de la razón a la serie correspondiente de valores absolutos. Para teoremas relacionados, vea los siguientes ejercicios: Ejercicio 2 y Ejercicio 4.

Teorema 9.7.1.2: Radio de convergencia de una serie de potencias

Supongamos que hay un número entero N tal que a_n ≠ 0 si n ≥ N y

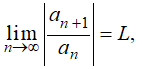
donde 0 ≤ L ≤ ∞. Entonces el radio de convergencia de 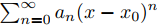es R = 1/L, lo que debe interpretarse como que R = 0  si  L = ∞, o  R = ∞  si  L = 0.  ♦

Ejemplo 9.7.1.1: Hallar el radio de convergencia de una serie de potencias

Encuentre el radio de convergencia de las series:

Solución:

(a)  Aquí a_n = n!, entonces

Por lo tanto, R = 0.

(b) Aquí a_n = (−1)ⁿ/n! para n ≥ N = 10, entonces

Por lo tanto, R = ∞.

(c) Aquí a_n = 2ⁿn², entonces

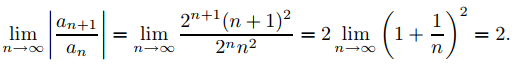
Por lo tanto, R = 1/2.  ♦

Series de Taylor

Si una función f tiene derivadas de todos los órdenes en un punto x = x₀, entonces la serie de Taylor de f alrededor de x₀ está definida por

En el caso especial donde x₀ = 0, esta serie también se llama la serie de Maclaurin de f.

      Las series de Taylor para la mayoría de las funciones elementales comunes convergen a las funciones en sus intervalos abiertos de convergencia. Por ejemplo, probablemente esté familiarizado con la siguientes series de Maclaurin:

Diferenciación de series de potencias

Una serie de potencias con un radio de convergencia positivo define una función

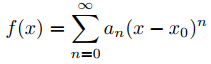
en su intervalo abierto de convergencia. Decimos que la serie representa f en el intervalo abierto de convergencia. Una función f representada por una serie de potencias puede ser una función elemental familiar como en (9.7.1.2) a (9.7.1.5); sin embargo, a menudo sucede que f no es una función familiar, por lo que la serie en realidad define f.

      El siguiente teorema muestra que una función representada por una serie de potencias tiene derivadas de todos los órdenes en el intervalo abierto de convergencia de la serie de potencias, y proporciona representaciones en serie de potencias de las derivadas.

Teorema 9.7.1.3: Derivadas de una serie de potencias

Una serie de potencias

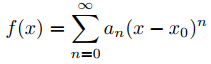
con radio de convergencia positivo R tiene derivadas de todos los órdenes en su intervalo abierto de convergencia, y se pueden obtener derivadas sucesivas diferenciando repetidamente término por término; esto es,

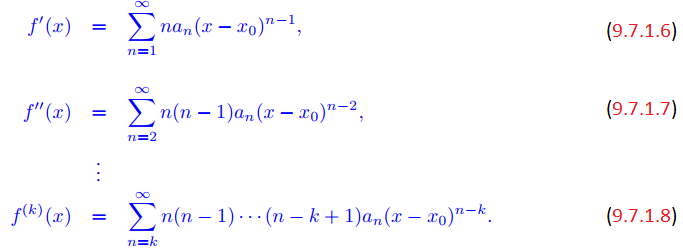
Además, todas estas series tienen el mismo radio de convergencia R.  ♦

Ejemplo 9.7.1.2: Derivada de la serie de potencias para senx

Sea f (x) = senx. De (9.7.1.3),

Desde (9.7.1.6)

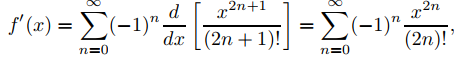
que es la serie (9.7.1.4) para cosx.  ♦

Unicidad de las series de potencias

El siguiente teorema muestra que si f está definida por una serie de potencias en x − x₀ con un radio de convergencia positivo, entonces la serie de potencias es la serie de Taylor de f alrededor de x₀.

Teorema 9.7.1.4: Serie de Taylor de f alrededor de x₀

Si la serie de potencias

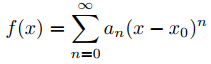
tiene un radio de convergencia positivo, entonces

      (9.7.1.9)

esto es, 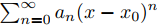es la serie de Taylor de f sobre x₀.   ♦

       Este resultado se puede obtener haciendo x = x₀ en (9.7.1.8), lo que da como resultado

f ^(k)(x₀) = k(k − 1) · · · 1 · a_k = k!a_k.

Esto implica que

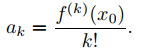
Excepto por la notación, esto es lo mismo que (9.7.1.9).

      El siguiente teorema enumera dos propiedades importantes de las series de potencias que se derivan del Teorema 9.7.1.4.

Teorema 9.7.1.5: Dos propiedades importantes de las series de potencias

(a) Si

para todo x en un intervalo abierto que contiene x₀, entonces a_n = b_n para n = 0, 1, 2, . . . .

(b) Si

para todo x en un intervalo abierto que contiene x₀, entonces a_n = 0 para n = 0, 1, 2, . . . .   ♦

      Para obtener (a) observamos que las dos series representan la misma función f en el intervalo abierto; por lo tanto, el Teorema 9.7.1.5 implica que

(b) puede obtenerse de (a) tomando b_n = 0 para n = 0, 1, 2, . . . .

Polinomios de Taylor

Si f tiene N derivadas en un punto x₀, decimos que

es el N-ésimo polinomio de Taylor de f sobre x₀. Esta definición y el Teorema 9.7.1.5 implican que si

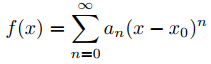donde la serie de potencias tiene un radio de convergencia positivo, entonces los polinomios de Taylor de f alrededor de x₀ están dados por

En aplicaciones numéricas, usamos los polinomios de Taylor para aproximar f en subintervalos del intervalo abierto de convergencia de la serie de potencias. Por ejemplo, (9.7.1.2) implica que el polinomio de Taylor T_N de f (x) = e^x es

La curva sólida de la figura 9.7.1.1 es la gráfica de y = e^x en el intervalo [0, 5]. Las curvas punteadas de la figura 9.7.1.1 son las gráficas de los polinomios de Taylor T₁, . . . , T₆ de y = e^x alrededor de x₀ = 0. A partir de esta figura, concluimos que la precisión de la aproximación de y = e^x por su polinomio de Taylor T_N mejora a medida que N aumenta.

Figura 9.7.1.1 Aproximación de y = e^x por polinomios de Taylor sobre x = 0

Desplazamiento del índice de suma

En la Definición 9.7.1.1 de una serie de potencias en x − x₀, el término n-ésimo es un múltiplo constante de (x − x₀)ⁿ. Esto no es cierto en (9.7.1.6), (9.7.1.7) y (9.7.1.8), donde los términos generales son múltiplos constantes de (x − x₀)ⁿ⁻¹, (x − x₀)^{n − 2} , y (x − x₀)^{n − k}, respectivamente. Sin embargo, todas estas series se pueden reescribir para que sus n-ésimos términos sean múltiplos constantes de (x − x₀)ⁿ. Por ejemplo, haciendo n = k + 1 en la serie en (9.7.1.6) se obtiene

      (9.7.1.10)

donde comenzamos el nuevo índice de suma k desde cero para que el primer término en (9.7.1.10) (obtenido al establecer k = 0) sea el mismo que el primer término en (9.7.1.6) (obtenido al establecer n = 1) . Sin embargo, la suma de una serie es independiente del símbolo usado para denotar el índice de suma, así como el valor de una integral definida es independiente del símbolo usado para denotar la variable de integración. Por lo tanto, podemos reemplazar k por n en (9.7.1.10) para obtener

      (9.7.1.11)

donde el término general es un múltiplo constante de (x − x₀)ⁿ.

      No es realmente necesario introducir el índice de suma intermedio k. Podemos obtener (9.7.1.11) directamente de (9.7.1.6) reemplazando n por n + 1 en el término general de (9.7.1.6) y restando 1 del límite inferior de (9.7.1.6). De manera más general, usamos el siguiente procedimiento para cambiar los índices.

Desplazamiento del índice de suma en una serie de potencias

Para cualquier entero k, la serie de potencias

se puede reescribir como

es decir, reemplazar n por n + k en el término general y restar k del límite inferior de la suma deja la serie sin cambios. ♦ 

---

Ejemplo 9.7.1.3: Corrimiento del índice de una serie de potencias 1

Reescriba la siguiente serie de potencias de (9.7.1.7) y (9.7.1.8) para que el término general en cada uno sea un múltiplo constante de (x − x₀)ⁿ:

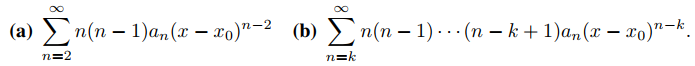
Solución:

(a) Reemplazando n por n + 2 en el término general y restando 2 del límite inferior de la sumatoria se obtiene

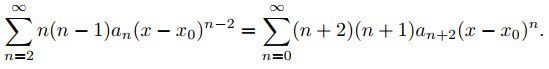
(b) Reemplazando n por n + k en el término general y restando k del límite inferior de la sumatoria se obtiene

♦

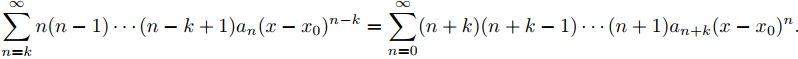Ejemplo 9.7.1.4: Corrimiento del índice de una serie de potencias 2

Dado que

escribe la función xf ′′ como una serie de potencias en la que el término general es un múltiplo constante de xⁿ.

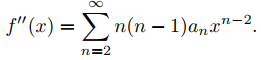
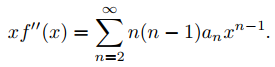
Combinaciones lineales de series de potencias

Si una serie de potencias se multiplica por una constante, entonces la constante se puede colocar dentro de la sumatoria; esto es,

Dos series de potencias

   y   

con radios de convergencia positivos se pueden sumar término a término en puntos comunes a sus intervalos abiertos de convergencia; por tanto, si la primera serie converge para |x − x₀| < R₁ y el segundo converge para |x − x₀| < R₂, entonces

para |x − x₀| < R, donde R es el menor de R₁ y R₂. De manera más general, las combinaciones lineales de series de potencias se pueden formar término por término; por ejemplo,

Ejemplo 9.7.1.5: Serie de Maclaurin para coshx

Encuentre la serie de Maclaurin para coshx como una combinación lineal de la serie de Maclaurin para e^x y e^−x.

Solución:
Por definición,

Ya que

   y 

resulta que

        (9.7.1.12)

Debido a que

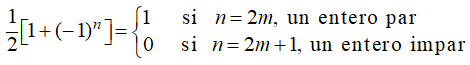
podemos reescribir (9.7.1.12) más simplemente como

Este resultado es válido en (−∞, ∞), ya que este es el intervalo abierto de convergencia de la serie de Maclaurin para e^x y e^−x.  ♦

Ejemplo 9.7.1.6

Suponer

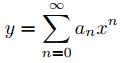
en un intervalo abierto I que contiene el origen.

(a) Expresar

(2 − x)y′′ + 2y

como una serie de potencias en x sobre I.

(b) Utilice el resultado de (a) para encontrar las condiciones necesarias y suficientes en los coeficientes {a_n} para que y sea una solución de la ecuación homogénea

(2 − x)y′′ + 2y = 0      (9.7.1.13)

en I.

Solución:

(a) De (9.7.1.7) con x₀ = 0,

Por lo tanto

      (9.7.1.14)

Para combinar las tres series, cambiamos los índices de las dos primeras para hacer que sus términos generales sean múltiplos constantes de xⁿ; de este modo,

      (9.7.1.15)

y

      (9.7.1.16)

donde agregamos un término cero en la última serie para que cuando sustituyamos (9.7.1.15) y (9.7.1.16) en (9.7.1.14) las tres series comiencen con n = 0; de este modo,

      (9.7.1.17)

(b) De (9.7.1.17) vemos que y satisface (9.7.1.13) en I si

2(n + 2)(n + 1)a_{n + 2} − (n + 1)ⁿa_n+1 + 2a_n = 0,  n = 0, 1, 2, . . ..        (9.7.1.18)

Por el contrario, el Teorema 9.7.1.6 (b) implica que si satisface (9.7.1.13) en I, entonces (9.7.1.18) se cumple.  ♦

Ejemplo 9.7.1.7

Suponer

en un intervalo abierto I que contiene x₀ = 1. Exprese la función

(1 + x)y′′ + 2(x − 1)2y′ + 3y        (9.7.1.19)

como una serie de potencias en x − 1 sobre I.

Solución:

Como queremos una serie de potencias en x − 1, reescribimos el coeficiente de y′′ en (9.7.1.19) como 1 + x = 2 + (x − 1), por lo que (9.7.1.19) se convierte en

2y′′ + (x − 1)y′′ + 2(x − 1)2y′ + 3y.

De (9.7.1.6) y (9.7.1.7) con x₀ = 1,

  y 

Por lo tanto

Antes de sumar estas cuatro series, cambiamos los índices de las tres primeras para que sus términos generales se conviertan en múltiplos constantes de (x − 1)ⁿ. Esto produce

donde agregamos términos cero iniciales a la serie en (9.7.1.21) y (9.7.1.22). Sumando (9.7.1.20) – (9.7.1.23) se obtiene

donde

b₀ = 4a₂ + 3a₀,        (9.7.1.24)
b_n = 2(n + 2)(n + 1)a_n+2 + (n + 1)ⁿa_n+1 + 2(n − 1)a_n−1 + 3a_n,  n ≥ 1.         (9.7.1.25)  ♦