| 4. Aplicaciones de la derivada | Ejercicios propuestos para el Capítulo 4.7 |
4.7 Problemas de optimización
Objetivos de aprendizaje:
4.7.1. Configurar y resolver problemas de optimización en varios campos de aplicación.
Una aplicación común en cálculo es hallar el valor mínimo o máximo de una función. Por ejemplo, las empresas a menudo quieren minimizar los costos de producción o maximizar los ingresos. En la fabricación, a menudo es deseable minimizar la cantidad de material utilizado para empaquetar un producto con un cierto volumen. En esta sección, mostramos cómo configurar estos tipos de problemas de minimización y maximización y resolverlos utilizando las herramientas desarrolladas en este capítulo.
Solución de problemas de optimización en un intervalo cerrado y acotado
La idea básica que siguen los problemas de optimización es básicamente la misma. Tenemos una cantidad particular que estamos interesados en maximizar o minimizar. Sin embargo, también tenemos algunas condiciones auxiliares que deben cumplirse. Por ejemplo, en el siguiente problema, estamos interesados en maximizar el área de un jardín rectangular. Ciertamente, si seguimos agrandando las longitudes laterales del jardín, el área continuará haciéndose más grande. Sin embargo, ¿qué pasa si tenemos alguna restricción sobre la cantidad de cercas que podemos usar para el perímetro? En este caso, no podemos hacer que el jardín sea tan grande como queramos. Veamos cómo podemos maximizar el área de un rectángulo sujeto a alguna restricción en el perímetro.
Ejemplo ilustrativo 4.7.1: Maximizando el área de un jardín
Se construirá un jardín rectangular utilizando una pared de roca como un lado del jardín y cercas de alambre para los otros tres lados (Figura 4.7.1). Dados 100 pies de cercas de alambre, determine las dimensiones que crearían un jardín de área máxima. Cuál es el área máxima?

Figura 4.7.1 Queremos determinar las medidas x e y que crearán un jardín con un área máxima utilizando 100 pies de cercado.
Solución:
Sea \(x\) la longitud del lado del jardín perpendicular a la pared de roca e \(y\) la longitud del lado paralelo a la pared de roca. Entonces, el área del jardín es
\(A = x \cdot y\).
Queremos encontrar el área máxima posible sujeta a la restricción de que la valla total es de 100 pies. De la Figura 4.7.1, la cantidad total de valla utilizada será \(2x + y\). Por lo tanto, la ecuación de restricción es
\(2x + y = 100\).
Resolviendo esta ecuación para \(y\), tenemos \(y = 100 – 2x\). Por lo tanto, podemos escribir el área como
\(A(x) = x \cdot (100 – 2x) = 100x – 2x^2\).
Antes de intentar maximizar la función de área \(A(x) = 100x – 2x^2\), necesitamos determinar el dominio en consideración. Para construir un jardín rectangular, ciertamente necesitamos que las longitudes de ambos lados sean positivas. Por lo tanto, necesitamos \(x > 0\) e \(y > 0\). Dado que \(y = 100 – 2x\), si \(y > 0\) entonces \(x < 50\). Por lo tanto, estamos tratando de determinar el valor máximo de \(A(x)\) para \(x\) en el intervalo abierto \((0, 50)\). No sabemos que una función necesariamente tenga un valor máximo sobre un intervalo abierto. Sin embargo, sí sabemos que una función continua tiene un máximo absoluto (y un mínimo absoluto) sobre un intervalo cerrado. Por lo tanto, consideremos la función \(A(x) = 100x - 2x^2\) sobre el intervalo cerrado \([0, 50]\). Si el valor máximo ocurre en un punto interior, entonces hemos encontrado el valor \(x\) en el intervalo abierto \((0, 50)\) que maximiza el área del jardín. Por lo tanto, consideramos el siguiente problema:
Maximizar \(A(x) = 100x – 2x^2\) sobre el intervalo \([0, 50]\).
Como se mencionó anteriormente, dado que \(A\) es una función continua en un intervalo cerrado y acotado, por el teorema del valor extremo, tiene un máximo y un mínimo. Estos valores extremos ocurren en los extremos o en los puntos críticos. En los extremos, \(A(x) = 0\). Dado que el área es positiva para todas las \(x\) en el intervalo abierto \((0, 50)\), el máximo debe ocurrir en un punto crítico. Derivando la función \(A(x)\) obtenemos
\(A'(x) = 100 – 4x\).
Por lo tanto, el único punto crítico es \(x = 25\) (Figura 4.7.2). Concluimos que el área máxima debe ocurrir cuando \(x = 25\). Entonces tenemos \(y = 100 – 2x = 100 – 2(25) = 50\). Para maximizar el área del jardín, sea \(x = 25\) pies e \(y = 50\) pies. El área de este jardín es \(1250\) pies\(^2\).

Figura 4.7.2 Para maximizar el área del jardín, necesitamos encontrar el valor máximo de la función A(x) = 100x − 2x2.
Ejercicio de control 4.7.1
Determina el área máxima si queremos hacer el mismo jardín rectangular que en la Figura 4.7.1, pero tenemos 200 pies de valla. ♦
Ahora veamos una estrategia general para resolver problemas de optimización similares al Ejemplo 4.7.1.
Estrategia de resolución de problemas: Resolver problemas de optimización
1. Identifique todas las variables involucradas en el problema. Si corresponde, dibuje una figura ilustrativa y etiquete todas las variables (asigne una letra que represente cada variable).
2. Determine qué cantidad se debe maximizar o minimizar y para qué rango de valores de las otras variables (si esto se puede determinar en este momento).
3. Escriba una fórmula para la cantidad a maximizar o minimizar en términos de las variables. Esta fórmula puede involucrar más de una variable independiente.
4. Escriba cualquier ecuación que relacione las variables independientes en la fórmula del paso 3. Use estas ecuaciones para escribir la cantidad que se maximizará o minimizará en función de una sola variable independiente.
5. Identifique el dominio de consideración para la función en el paso 4 en relación del problema físico a resolver.
6. Calcule el valor máximo o mínimo de la función obtenida en el paso 4. Este paso generalmente implica buscar puntos críticos y evaluar la función en los puntos finales. ♦
Ahora apliquemos esta estrategia para maximizar el volumen de una caja sin tapa dada una restricción en la cantidad de material a utilizar.
Ejemplo ilustrativo 4.7.2: Maximizando el Volumen de una Caja
Se va a hacer una caja sin tapa a partir de un trozo de cartón de 24 pulgadas por 36 pulgadas, cortando un cuadrado de cada esquina de la caja y doblando las solapas de cada lado. ¿Qué tamaño de cuadrado se debe cortar de cada esquina para obtener una caja con el volumen máximo?
Solución:
Paso 1: Sea x la longitud del lado del cuadrado que se va a quitar de cada esquina (Figura 4.7.3). Luego, las cuatro solapas restantes se pueden doblar para formar una caja sin tapa. Sea V el volumen de la caja resultante.
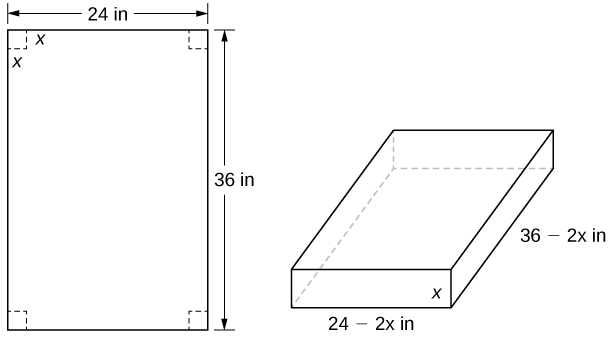
Figura 4.7.3 Se retira un cuadrado con una longitud de lado x pulgadas (in) de cada esquina del trozo de cartón. Las solapas restantes se doblan para formar una caja sin tapa.
Paso 2: Estamos tratando de maximizar el volumen de una caja. Por lo tanto, el problema es maximizar V.
Paso 3: Como se mencionó en el paso 2, estamos tratando de maximizar el volumen de una caja. El volumen de una caja es \(V = L \cdot W \cdot H\), donde L, W y H son la longitud, el ancho y la altura, respectivamente.
Paso 4: De la Figura 4.7.3, vemos que la altura de la caja es \(x\) pulgadas, la longitud es \(36 – 2x\) pulgadas y el ancho es \(24 – 2x\) pulgadas. Por lo tanto, el volumen de la caja es
\(V(x) = (36 – 2x)(24 – 2x)x = 4x^3 – 120x^2 + 864x\).
Paso 5: Para determinar el dominio en consideración, examinemos la Figura 4.64. Ciertamente, necesitamos \(x > 0\). Además, la longitud del lado del cuadrado no puede ser mayor o igual a la mitad de la longitud del lado más corto, 24 pulgadas; de lo contrario, una de las solapas se cortaría por completo. Por lo tanto, estamos tratando de determinar si existe un volumen máximo de la caja para \(x\) en el intervalo abierto \((0, 12)\). Dado que \(V\) es una función continua en el intervalo cerrado \([0, 12]\), sabemos que \(V\) tendrá un máximo absoluto en el intervalo cerrado. Por lo tanto, consideramos \(V\) en el intervalo cerrado \([0, 12]\) y verificamos si el máximo absoluto ocurre en un punto interior.
Paso 6: Dado que \(V(x)\) es una función continua en el intervalo cerrado y acotado \([0, 12]\), \(V\) debe tener un máximo absoluto (y un mínimo absoluto). Dado que \(V(x) = 0\) en los extremos y \(V(x) > 0\) para \(0 < x < 12\), el máximo debe ocurrir en un punto crítico. La derivada es
\(V'(x) = 12x^2 – 240x + 864\).
Para encontrar los puntos críticos, necesitamos resolver la ecuación
\(12x^2 – 240x + 864 = 0\).
Dividiendo ambos lados de esta ecuación por 12, el problema se simplifica a resolver la ecuación
\(x^2 – 20x + 72 = 0\).
Usando la fórmula cuadrática, encontramos que los puntos críticos son
\(x = \frac{20 \pm \sqrt{(-20)^2 – 4(1)(72)}}{2} = \frac{20 \pm \sqrt{112}}{2} = \frac{20 \pm 4\sqrt{7}}{2} = 10 \pm 2\sqrt{7}\).
Dado que \(10 + 2\sqrt{7}\) no está en el dominio en consideración, el único punto crítico que debemos considerar es \(10 – 2\sqrt{7}\). Por lo tanto, el volumen se maximiza si dejamos que \(x = 10 – 2\sqrt{7}\) pulgadas. El volumen máximo es \(V(10 – 2\sqrt{7}) = 640 + 448\sqrt{7} \approx 1825\) pulgadas\(^3\) como se muestra en el siguiente gráfico.
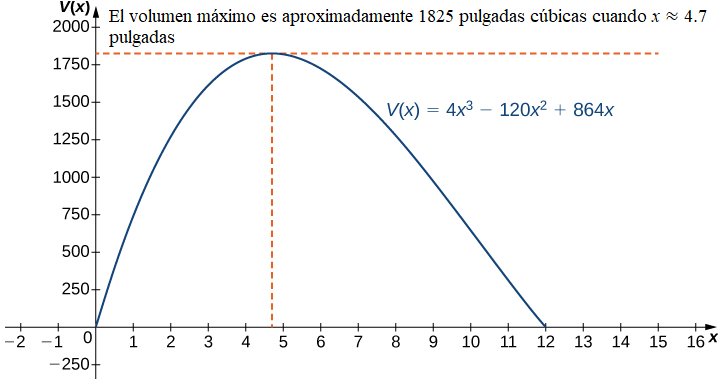
Figura 4.7.4 Maximizar el volumen de la caja lleva a encontrar el valor máximo de un polinomio cúbico. ♦
Ejercicio de control 4.7.2
Suponga que las dimensiones del cartón en el Ejemplo 4.7.2 son 20 pulgadas por 30 pulgadas. Sea x la longitud del lado de cada cuadrado y escriba el volumen de la caja sin tapa como una función de x. Determine el dominio de consideración para x. ♦
Ejemplo ilustrativo 4.7.3: Minimizar el tiempo de viaje
Una isla está a 2 millas directamente al norte de su punto más cercano a lo largo de una costa recta. Un visitante se hospeda en una cabaña en la costa que está a 6 millas al oeste de ese punto. El visitante planea ir desde la cabaña a la isla. Suponga que el visitante corre a una velocidad de 8 mph y nada a una velocidad de 3 mph. ¿Qué tan lejos debe correr el visitante antes de nadar para minimizar el tiempo que tarda en llegar a la isla?
Solución:
Paso 1: Sea x la distancia que corre y sea y la distancia que nada (Figura 4.7.5). Sea T el tiempo que tarda en llegar desde la cabaña a la isla.
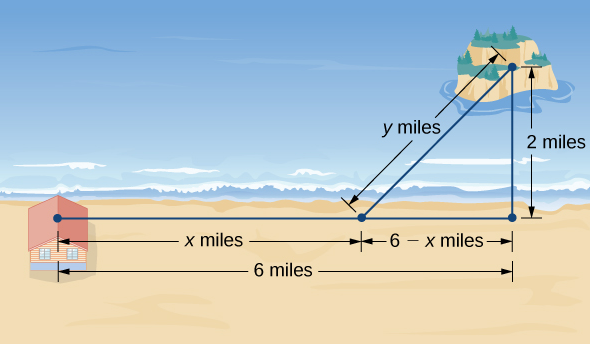
Figura 4.7.5 ¿Cómo podemos elegir x e y para minimizar el tiempo de viaje desde la cabaña hasta la isla?
Paso 2: El problema es minimizar T.
Paso 3: Para encontrar el tiempo empleado en viajar desde la cabaña hasta la isla, sume el tiempo empleado corriendo y el tiempo empleado nadando. Dado que Distancia = Velocidad × Tiempo (D = R × T), el tiempo empleado corriendo es
\(T_{corriendo} = \frac{D_{corriendo}}{R_{corriendo}} = \frac{x}{8}\),
y el tiempo empleado nadando es
\(T_{nadando} = \frac{D_{nadando}}{R_{nadando}} = \frac{y}{3}\).
Por lo tanto, el tiempo total empleado en viajar es
\(T = \frac{x}{8} + \frac{y}{3}\).
Paso 4: De la Figura 4.66, el segmento de línea de \(y\) millas forma la hipotenusa de un triángulo rectángulo con catetos de longitud 2 mi y \(6-x\) mi. Por lo tanto, por el teorema de Pitágoras, \(2^2 + (6-x)^2 = y^2\), y obtenemos \(y = \sqrt{(6-x)^2 + 4}\). Por lo tanto, el tiempo total empleado en viajar está dado por la función
\(T(x) = \frac{x}{8} + \frac{\sqrt{(6-x)^2 + 4}}{3}\).
Paso 5: De la Figura 4.66, vemos que \(0 \le x \le 6\). Por lo tanto, \([0, 6]\) es el dominio en consideración.
Paso 6: Dado que \(T(x)\) es una función continua en un intervalo cerrado y acotado, tiene un máximo y un mínimo. Comencemos buscando puntos críticos de \(T\) en el intervalo \([0, 6]\). La derivada es
\(T'(x) = \frac{1}{8} – \frac{1}{2}[(6-x)^2 + 4]^{-1/2} \cdot 2(6-x) = \frac{1}{8} – \frac{(6-x)}{3\sqrt{(6-x)^2 + 4}}\).
Si \(T'(x) = 0\), entonces
\(\frac{1}{8} = \frac{6-x}{3\sqrt{(6-x)^2 + 4}}\).
Por lo tanto,
\(3\sqrt{(6-x)^2 + 4} = 8(6-x)\).
(4.7.1)
Elevando al cuadrado ambos lados de esta ecuación, vemos que si \(x\) satisface esta ecuación, entonces \(x\) debe satisfacer
\(9[(6-x)^2 + 4] = 64(6-x)^2\),
lo que implica
\(55(6-x)^2 = 36\).
Concluimos que si \(x\) es un punto crítico, entonces \(x\) satisface
\((x-6)^2 = \frac{36}{55}\).
Por lo tanto, las posibilidades para los puntos críticos son
\(x = 6 \pm \frac{6}{\sqrt{55}}\).
Dado que \(x = 6 + \frac{6}{\sqrt{55}}\) no está en el dominio, no es una posibilidad para un punto crítico. Por otro lado, \(x = 6 – \frac{6}{\sqrt{55}}\) está en el dominio. Dado que elevamos al cuadrado ambos lados de la Ecuación 4.7.1 para llegar a los posibles puntos críticos, queda por verificar que \(x = 6 – \frac{6}{\sqrt{55}}\) satisface la Ecuación 4.7.1. Dado que \(x = 6 – \frac{6}{\sqrt{55}}\) satisface esa ecuación, concluimos que \(x = 6 – \frac{6}{\sqrt{55}}\) es un punto crítico, y es el único. Para justificar que el tiempo se minimiza para este valor de \(x\), solo necesitamos verificar los valores de \(T(x)\) en los extremos \(x = 0\) y \(x = 6\), y compararlos con el valor de \(T(x)\) en el punto crítico \(x = 6 – \frac{6}{\sqrt{55}}\). Encontramos que \(T(0) \approx 2.108\) h y \(T(6) \approx 1.417\) h, mientras que \(T(6 – \frac{6}{\sqrt{55}}) \approx 1.368\) h. Por lo tanto, concluimos que \(T\) tiene un mínimo local en \(x \approx 5.19\) mi. ♦
Ejercicio de control 4.7.3
Suponga que la isla está a 1 milla (mi) de la costa, y la distancia desde la cabaña hasta el punto en la costa más cercano a la isla es de 15 millas (mi). Suponga que un visitante nada a una velocidad de 2.5 mph y corre a una velocidad de 6 mph. Sea x la distancia que el visitante correrá antes de nadar, y encuentre una función para el tiempo que le toma al visitante llegar desde la cabaña a la isla. ♦
En los negocios, las empresas están interesadas en maximizar los ingresos. En el siguiente ejemplo, consideramos un escenario en el que una empresa ha recopilado datos sobre cuántos coches puede arrendar, dependiendo del precio que cobra a sus clientes por alquilar un coche. Usemos estos datos para determinar el precio que la empresa debe cobrar para maximizar la cantidad de dinero que recauda.
Ejemplo ilustrativo 4.7.4: Maximizar los ingresos
Los dueños de una empresa de alquiler de coches han determinado que si cobran a los clientes p dólares por día por alquilar un coche, donde 50≤p≤200, el número de coches n que alquilan por día se puede modelar mediante la función lineal n(p)=1000–5p.

Solución;
Paso 1: Sea \(p\) el precio cobrado por coche por día y sea \(n\) el número de coches alquilados por día. Sea \(R\) los ingresos por día.
Paso 2: El problema es maximizar \(R\).
Paso 3: Los ingresos (por día) son iguales al número de coches alquilados por día multiplicado por el precio cobrado por coche por día, es decir, \(R = n \times p\).
Paso 4: Dado que el número de coches alquilados por día está modelado por la función lineal \(n(p) = 1000 – 5p\), los ingresos \(R\) se pueden representar mediante la función
\(R(p) = n \times p = (1000 – 5p)p = -5p^2 + 1000p\).
Paso 5: Dado que los propietarios planean cobrar entre $50 por coche por día y $200 por coche por día, el problema es encontrar los ingresos máximos \(R(p)\) para \(p\) en el intervalo cerrado \([50, 200]\).
Paso 6: Dado que \(R\) es una función continua en el intervalo cerrado y acotado \([50, 200]\), tiene un máximo absoluto (y un mínimo absoluto) en ese intervalo. Para encontrar el valor máximo, busca puntos críticos. La derivada es \(R'(p) = -10p + 1000\). Por lo tanto, el punto crítico es \(p = 100\). Cuando \(p = 100\), \(R(100) = \$50,000\). Cuando \(p = 50\), \(R(p) = \$37,500\). Cuando \(p = 200\), \(R(p) = \$0\). Por lo tanto, el máximo absoluto ocurre en \(p = \$100\). La empresa de alquiler de coches debería cobrar $100 por día por coche para maximizar los ingresos, como se muestra en la siguiente figura.
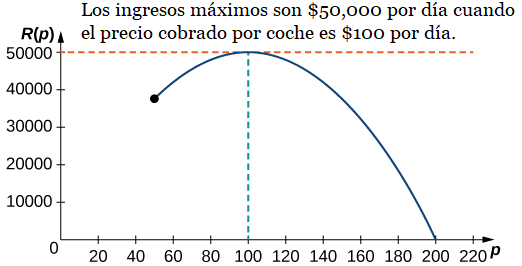
Figura 4.7.6 Para maximizar los ingresos, una empresa de alquiler de coches tiene que equilibrar el precio de un alquiler con la cantidad de coches que la gente alquilará a ese precio.
Ejercicio de control 4.7.4
Una empresa de alquiler de coches cobra a sus clientes p dólares por día, donde 60 ≤ p ≤ 150. Ha descubierto que el número de coches alquilados por día se puede modelar mediante la función lineal n(p) = 750 – 5p. ¿Cuánto debería cobrar la empresa a cada cliente para maximizar los ingresos? ♦
Ejemplo ilustrativo 4.7.5: Maximizando el Área de un Rectángulo Inscrito
Se va a inscribir un rectángulo en la elipse \[\frac{x^{2}}{4}+y^{2}=1.\] ¿Cuáles deberían ser las dimensiones del rectángulo para maximizar su área? ¿Cuál es el área máxima?
Solución:
Paso 1: Para que un rectángulo esté inscrito en la elipse, los lados del rectángulo deben ser paralelos a los ejes. Sea L la longitud del rectángulo y W su ancho. Sea A el área del rectángulo.
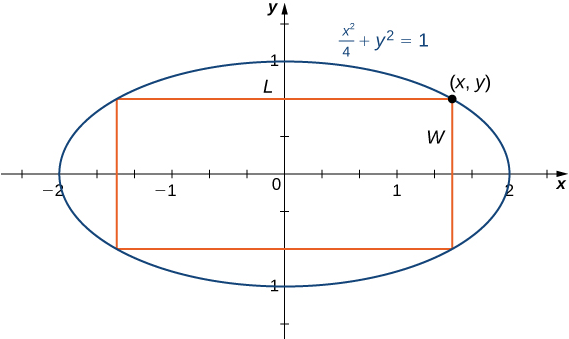
Figura 4.7.7 Queremos maximizar el área de un rectángulo inscrito en una elipse.
Paso 2: El problema es maximizar A.
Paso 3: El área del rectángulo es A = LW.
Paso 4: Sea \((x,y)\) la esquina del rectángulo que se encuentra en el primer cuadrante, como se muestra en la Figura 4.7.7. Podemos escribir la longitud \(L=2x\) y el ancho \(W=2y\). Dado que \(\frac{x^2}{4}+y^2=1\) e \(y>0\), tenemos \(y=\sqrt{1-\frac{x^2}{4}}\). Por lo tanto, el área es
\(A=LW=(2x)(2y)=4x\sqrt{1-\frac{x^2}{4}}=2x\sqrt{4-x^2}\).
Paso 5: De la Figura 4.7.7, vemos que para inscribir un rectángulo en la elipse, la coordenada x de la esquina en el primer cuadrante debe satisfacer \(0 Paso 6: Como se mencionó anteriormente, \(A(x)\) es una función continua en el intervalo cerrado y acotado \([0,2]\). Por lo tanto, tiene un máximo absoluto (y un mínimo absoluto). En los extremos \(x=0\) y \(x=2\), \(A(x)=0\). Para \(0
\(
\begin{aligned}
A'(x) &= 2\sqrt{4-x^2}+2x\cdot\frac{1}{2\sqrt{4-x^2}}(-2x) \\
&= 2\sqrt{4-x^2}-\frac{2x^2}{\sqrt{4-x^2}} \\
&= \frac{8-4x^2}{\sqrt{4-x^2}}.
\end{aligned}
\)
Para encontrar puntos críticos, necesitamos encontrar dónde \(A'(x)=0\). Podemos ver que si \(x\) es una solución de \(\frac{8-4x^2}{\sqrt{4-x^2}}=0\), entonces \(x\) debe satisfacer \(8-4x^2=0\). Por lo tanto, \(x^2=2\). Así, \(x=\pm\sqrt{2}\) son las posibles soluciones de la ecuación anterior. Dado que estamos considerando \(x\) en el intervalo \([0,2]\), \(x=\sqrt{2}\) es una posibilidad para un punto crítico, pero \(x=-\sqrt{2}\) no lo es. Por lo tanto, verificamos si \(\sqrt{2}\) es una solución de la ecuación anterior. Dado que \(x=\sqrt{2}\) es una solución, concluimos que \(\sqrt{2}\) es el único punto crítico de \(A(x)\) en el intervalo \([0,2]\). Por lo tanto, \(A(x)\) debe tener un máximo absoluto en el punto crítico \(x=\sqrt{2}\). Para determinar las dimensiones del rectángulo, necesitamos encontrar la longitud L y el ancho W. Si \(x=\sqrt{2}\) entonces \(y=\sqrt{1-\frac{(\sqrt{2})^2}{4}}=\sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}\). Por lo tanto, las dimensiones del rectángulo son \(L=2x=2\sqrt{2}\) y \(W=2y=\frac{2}{\sqrt{2}}=\sqrt{2}\). El área de este rectángulo es \(A=LW=(2\sqrt{2})(\sqrt{2})=4\). ♦ Modifique la función de área A si el rectángulo va a ser inscrito en el círculo unitario x2 + y2 = 1. ¿Cuál es el dominio a considerar? ♦ En los ejemplos anteriores, consideramos funciones en
dominios cerrados y acotados. En consecuencia, por el teorema del valor
extremo, se nos garantizó que las funciones tenían extremos absolutos.
Consideremos ahora las funciones para las cuales el dominio no está cerrado ni
limitado. Muchas funciones todavía tienen al menos un extremo absoluto, incluso si el dominio no está cerrado o el dominio no tiene límites. Por ejemplo, la función f (x) = x2 + 4 sobre (−∞, ∞) tiene un mínimo absoluto de 4 en x = 0. Por lo tanto, aún podemos considerar funciones sobre dominios ilimitados o intervalos abiertos y determinar si tienen algún extremo absoluto. En el siguiente ejemplo, tratamos de minimizar una función sobre un dominio ilimitado. Veremos que, aunque el dominio de consideración es (0, ∞), la función tiene un mínimo absoluto. En la solución del problema ilustrativo que sigue, observamos la construcción de una caja de menor superficie con un volumen prescrito. No es difícil demostrar que, para una caja superior cerrada, por simetría, entre todas las cajas con un volumen especificado, un cubo tendrá el área de superficie más pequeña. En consecuencia, consideramos el problema modificado de determinar qué caja abierta con un volumen especificado tiene el área de superficie más pequeña. Se construirá una caja rectangular con una base cuadrada, una parte superior abierta y un volumen de 216 pulgadas. ¿Cuáles deberían ser las dimensiones de la caja para minimizar el área de superficie de la caja? ¿Cuál es el área de superficie mínima? Solución: Paso 1: Se dibuja una caja rectangular e introduce la variable x para representar la longitud de cada lado de la base cuadrada, en pulgadas; la letra y representa la altura de la caja, en plg. La letra S denota el área de superficie del cuadrado superior abierto, en pulgadas cuadradas. Paso 2:
Necesitamos minimizar el área de la superficie. Por lo tanto, debemos minimizar
S. Paso 3:
Dado que la caja tiene una parte superior abierta, solo necesitamos determinar
el área de los cuatro lados verticales y la base cuadrada. El área de cada uno
de los cuatro lados verticales es x⋅y. El área de la base es x2. Por lo tanto, el área de la
superficie de la caja es S = 4xy
+ x2. Paso 4:
Dado que el volumen de esta caja es x2 y y el volumen que se da es 216 plg.3,
la ecuación de restricción es x2 y = 216. Resolviendo la ecuación de restricción para y, tenemos y = 216/x2. Por lo tanto, podemos escribir el área de la superficie en función de la variable independiente x solamente: Paso 5:
Dado que estamos requiriendo que x2y = 216, no podemos tener x = 0. Por lo tanto, necesitamos x > 0. Por otro lado, x puede tener cualquier valor positivo.
Tenga en cuenta que a medida que x se
hace grande, la altura y de la caja se
hace correspondientemente pequeña, de modo que se cumpla x2y = 216. Del
mismo modo, a medida que x se vuelve
pequeña, la altura de la caja se vuelve correspondientemente grande. Llegamos a
la conclusión de que el dominio es el intervalo abierto, sin límites (0, ∞).
Tenga en cuenta que, a diferencia de los ejemplos anteriores, no podemos
reducir nuestro problema a buscar un máximo absoluto o un mínimo absoluto en un
intervalo cerrado y acotado. Sin embargo, en el siguiente paso, descubrimos por
qué esta función debe tener un mínimo absoluto durante el intervalo (0, ∞). Paso 6: Tenga en cuenta que cuando x → 0+, S (x) → ∞. Además, cuando x → ∞, S (x) → ∞. Como S es una función continua que se aproxima al infinito en los extremos, debe tener un mínimo absoluto en algún x ∈ (0, ∞). Este mínimo debe ocurrir en un punto crítico de S. La derivada de S es Por lo tanto, S‘ (x) = 0 cuando 2x = 864 / x2. Al resolver esta ecuación para x, obtenemos x3 = 432, entonces Como este es el único punto crítico de S, el mínimo absoluto debe ocurrir allí (ver Figura 4.38). Cuando Por lo tanto, las dimensiones de la caja deben ser Con estas dimensiones, el área de la superficie de la caja es Consideremos la misma caja abierta, que debe tener un volumen de 216 pulgadas cúbicas (216 in³). Suponga que el costo del material para la base es de 20¢/in² y el costo del material para los lados es de 30¢/in², y estamos tratando de minimizar el costo de esta caja. Escriba el costo como una función de las longitudes de los lados de la base. (Sea x la longitud del lado de la base e y la altura de la caja). ♦Ejercicio de control 4.7.5
Solución de problemas de optimización cuando el
intervalo no está cerrado o no está limitado
Ejemplo ilustrativo 4.7.6: Minimizando el Área de una Superficie

Figura 4.7.8 Queremos minimizar el área de superficie de una caja rectangular con un volumen dado.
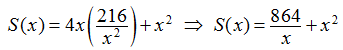
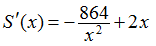
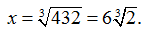

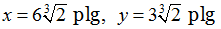


Figura 4.7.9 Podemos usar la gráfica de S para determinar las dimensiones de la caja y el área de superficie mínima dado el volumen. ♦
Ejercicio de control 4.7.6

¡Hurra! Por fin encontré una página web desde donde soy capaz de obtener genuinamente datos útiles sobre mi estudio y así obtener más conocimiento.