| 9. Ecuaciones diferenciales | 9.7. Soluciones en serie de ecuaciones lineales de segundo orden | Ejercicios propuestos para el Capítulo 9.7.4 |
9.7.4 Ecuaciones de Euler de puntos singulares regulares
| Esta sección prepara el escenario para las Secciones 9.7.5, 9.7.6 y 9.7.7. Si no está interesado en esas secciones, pero desea aprender sobre las ecuaciones de Euler, omita los párrafos introductorios y comience a leer en la Definición 9.7.4.2. |
En las próximas tres secciones continuaremos estudiando ecuaciones de la forma
P0(x)y′′ + P1(x)y′ + P2(x)y = 0 (9.7.4.1)
donde P0, P1 y P2 son polinomios, pero el énfasis será diferente al de las Secciones 9.7.2 y 9.7.3, donde obtuvimos soluciones de (9.7.4.1) cerca de un punto ordinario x0 en forma de serie de potencias en x − x0. Si x0 es un punto singular de (9.7.4.1) (es decir, si P(x0) = 0), las soluciones en general no pueden representarse mediante series de potencias en x − x0. Sin embargo, a menudo es necesario en aplicaciones físicas estudiar el comportamiento de las soluciones de (9.7.4.1) cerca de un punto singular. Aunque esto puede ser difícil en ausencia de algún tipo de suposición sobre la naturaleza del punto singular, las ecuaciones que satisfacen los requisitos de la siguiente definición se pueden resolver mediante métodos en serie discutidos en las siguientes tres secciones. Afortunadamente, muchas ecuaciones que surgen en las aplicaciones satisfacen estos requisitos.
Definición 9.7.4.1
Sean P0, P1 y P2 polinomios sin factor común y supongamos que P0(x0) = 0.
Entonces x0 es un punto singular regular de la ecuación
P0(x)y′′ + P1(x)y′ + P2(x)y = 0 (9.7.4.2)
si (9.7.4.2) se puede escribir como
(x − x0)2A(x)y′′ + (x − x0)B(x)y′ + C(x)y = 0 (9.7.4.3)
donde A, B y C son polinomios y A(x0) ≠ 0; de lo contrario, x0 es un punto singular irregular de (9.7.4.2). ♦
Ejemplo ilustrativo 9.7.4.1
La ecuación de Bessel,
x2y′′ + xy′ + (x2 − ν2)y = 0, (9.7.4.4)
tiene el punto singular x0 = 0. Dado que esta ecuación tiene la forma (9.7.4.3) con x0 = 0, A(x) = 1, B(x) = 1 y C(x) = x2 − ν2, se sigue que x0 = 0 es un punto singular regular de (9.7.4.4). ♦
Ejemplo ilustrativo 9.7.4.2
La ecuación de Legendre,
(1 − x2)y′′ − 2xy′ + α(α + 1)y = 0, (9.7.4.5)
tiene los puntos singulares x0 = ±1. Multiplicando por 1 − x se obtiene
(x − 1)2(x + 1)y′′ + 2x(x − 1)y′ − α(α + 1)(x − 1)y = 0,
que es de la forma (9.7.4.3) con x0 = 1, A(x) = x + 1, B(x) = 2x y C(x) = −α(α + 1)(x − 1). Por lo tanto x0 = 1 es un punto singular regular de (9.7.4.5). Te dejamos a ti demostrar que x0 = −1 también es un punto singular regular de (9.7.4.5). ♦
Ejemplo ilustrativo 9.7.4.3
La ecuación
x3y′′ + xy′ + y = 0
tiene un punto singular irregular en x0 = 0. (Compruebe). ♦
Por conveniencia restringimos nuestra atención al caso donde x0 = 0 es un punto singular regular de (9.7.4.2). Esto no es realmente una restricción, ya que si x0 ≠ 0 es un punto singular regular de (9.7.4.2), entonces se introduce la nueva variable independiente t = x − x0 y la nueva incógnita Y(t) = y(t + x0) conduce a una ecuación diferencial con coeficientes polinómicos que tiene un punto singular regular en t0 = 0. Esto se ilustra en el Ejercicio 22 para la ecuación de Legendre y en el Ejercicio 23 para el caso general.
Ecuaciones de Euler
El tipo de ecuación más simple con un punto singular regular en x0 = 0 es la ecuación de Euler, definida como sigue.
Definición 9.7.4.2
Una ecuación de Euler es una ecuación que se puede escribir en la forma
ax2y′′ + bxy′ + cy = 0, (9.7.4.6)
donde a, b y c son constantes reales y a ≠ 0. ♦
El Teorema 9.5.1.1 implica que (9.7.4.6) tiene soluciones definidas en (0, ∞) y (−∞, 0), ya que (9.7.4.6) se puede reescribir como

Por conveniencia restringiremos nuestra atención al intervalo (0, ∞). (El Ejercicio 19 trata con soluciones de (9.7.4.6) en (−∞, 0).) La clave para encontrar soluciones en (0, ∞) es que si x > 0 entonces xr se define como una función de valor real en ( 0, ∞) para todos los valores de r, y al sustituir y = xr en (9.7.4.6) se obtiene
 (9.7.4.7)
(9.7.4.7)
El polinomio
p(r) = ar(r − 1) + br + c
se llama el polinomio indicial de (9.7.4.6), y p(r) = 0 es su ecuación indicial. De (9.7.4.7) podemos ver que y = xr es una solución de (9.7.4.6) en (0, ∞) si y solo si p(r) = 0. Por lo tanto, si la ecuación indicial tiene distintas raíces reales r1 y r2 entonces  y
y  forman un conjunto fundamental de soluciones de (9.7.4.6) en (0, ∞), ya que
forman un conjunto fundamental de soluciones de (9.7.4.6) en (0, ∞), ya que 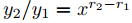 no es constante. En este caso
no es constante. En este caso

es la solución general de (9.7.4.6) en (0, ∞).
Ejemplo ilustrativo 9.7.4.4
Encuentre la solución general de
x2y′′ − xy′ − 8y = 0 (9.7.4.8)
en (0, ∞).
Solución:
El polinomio indicial de (9.7.4.8) es
p(r) = r(r − 1) − r − 8 = (r − 4)(r + 2).
Por lo tanto y1 = x4 y y2 = x−2 son soluciones de (9.7.4.8) en (0, ∞), y su solución general en (0, ∞) es
 ♦
♦
Ejemplo ilustrativo 9.7.4.5
Encuentre la solución general de
6x2y′′ + 5xy′ − y = 0 (9.7.4.9)
en (0, ∞).
Solución:
El polinomio indicial de (9.7.4.9) es
p(r) = 6r(r − 1) + 5r − 1 = (2r − 1)(3r + 1).
Por lo tanto la solución general de (9.7.4.9) en (0, ∞) es
 ♦
♦
Si la ecuación indicial tiene una raíz repetida r1, entonces y1 = xr1 es una solución de
ax2y′′ + bxy′ + cy = 0, (9.7.4.10)
en (0, ∞), pero (9.7.4.10) no tiene otra solución de la forma y = xr. Si la ecuación indicial tiene ceros complejos conjugados, entonces (9.7.4.10) no tiene soluciones con valores reales de la forma y = xr. Afortunadamente podemos usar los resultados de la Sección 9.5.2 para ecuaciones de coeficientes constantes para resolver (9.7.4.10) en cualquier caso.
Teorema 9.7.4.1
Supongamos que las raíces de la ecuación indicial
ar(r − 1) + br + c = 0 (9.7.4.11)
son r1 y r2. Entonces la solución general de la ecuación de Euler
ax2y′′ + bxy′ + cy = 0 (9.7.4.12)
en (0, ∞) es
 si r1 y r2 son números reales distintos;
si r1 y r2 son números reales distintos; si r1 = r2 ;
si r1 = r2 ; si r1, r2 = λ ± iω con ω > 0. ♦
si r1, r2 = λ ± iω con ω > 0. ♦
Prueba:
Primero demostramos que y = y(x) satisface (9.7.4.12) en (0, ∞) si y solo si Y(t) = y(et) satisface la ecuación de coeficientes constantes
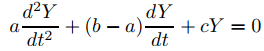 (9.7.4.13)
(9.7.4.13)
en (−∞, ∞). Para ello, es conveniente escribir x = et, o lo que es lo mismo, t = lnx; así, Y(t) = y(x), donde x = et. De la regla de la cadena
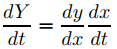
y desde

resulta que
 (9.7.4.14)
(9.7.4.14)
Derivando esto con respecto a t y usando la regla de la cadena nuevamente se obtiene
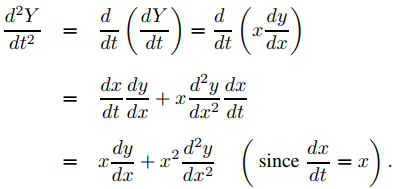
De esto y (9.7.4.14),

Sustituyendo esto y (9.7.4.14) en (9.7.4.12) se obtiene (9.7.4.13). Como (9.7.4.11) es la ecuación característica de (9.7.4.13), el Teorema 9.5.2.1 implica que la solución general de (9.7.4.13) en (−∞, ∞) es
 si r1 y r2 son números reales distintos;
si r1 y r2 son números reales distintos; si r1 = r2;
si r1 = r2; si r1, r2 = λ ± iω con ω ∕= 0.
si r1, r2 = λ ± iω con ω ∕= 0.
Como Y(t) = y(et), al sustituir t = lnx en las últimas tres ecuaciones se muestra que la solución general de (9.7.4.12) en (0, ∞) tiene la forma establecida en el teorema. ♦
Ejemplo ilustrativo 9.7.4.6
Encuentre la solución general de
x2y′′ − 5xy′ + 9y = 0 (9.7.4.15)
en (0, ∞).
Solución:
El polinomio indicial de (9.7.4.15) es
p(r) = r(r − 1) − 5r + 9 = (r − 3)2.
Por lo tanto la solución general de (9.7.4.15) en (0, ∞) es
y = x3(c1 + c2 lnx). ♦
Ejemplo ilustrativo 9.7.4.7
Encuentre la solución general de
x2y′′ + 3xy′ + 2y = 0 (9.7.4.16)
en (0, ∞).
Solución:
El polinomio indicial de (9.7.4.16) es
p(r) = r(r − 1) + 3r + 2 = (r + 1)2 + 1.
Las raíces de la ecuación indicial son r = −1 ± i y la solución general de (9.7.4.16) en (0, ∞) es
 ♦
♦

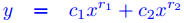 si r1 y r2 son números reales distintos;
si r1 y r2 son números reales distintos; si r1 = r2 ;
si r1 = r2 ; si r1, r2 = λ ± iω con ω > 0.
si r1, r2 = λ ± iω con ω > 0.