| 9. Ecuaciones diferenciales | 9.5. Ecuaciones lineales de segundo orden | Ejercicios propuestos para el Capítulo 9.5.6 |
9.5.6 Reducción de orden
En esta sección damos un método para encontrar la solución general de
P0(x)y″ + P1(x)y′ + P2(x)y = F(x) (9.5.6.1)
si conocemos una solución no trivial y1 de la ecuación complementaria
P0(x)y″ + P1(x)y′ + P2(x)y = 0 (9.5.6.2)
El método se llama reducción de orden porque reduce la tarea de resolver (9.5.6.1) a resolver una ecuación de primer orden. A diferencia del método de coeficientes indeterminados, no requiere que P0, P1 y P2 sean constantes, ni que F tenga una forma especial.
A estas alturas no debería sorprenderte que busquemos soluciones de (9.5.6.1) de la forma
y = uy1 (9.5.6.3)
donde u debe determinarse de modo que y satisfaga (9.5.6.1). Sustituyendo (9.5.6.3) y las derivadas
y′ = u′y1 + uy′1
y″ = u″y1 + 2u′y′ + uy1″
en (9.5.6.1), se obtiene
Al agrupar los coeficientes de u, u′ y u″, obtenemos
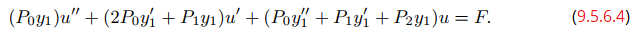
Sin embargo, el coeficiente de u es cero, ya que y1 satisface (9.5.6.2). Por lo tanto (9.5.6.4) se reduce a
(9.5.6.5)
con
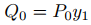y 
(¡No vale la pena memorizar las fórmulas para Q0 y Q1!) Dado que (9.5.6.5) es una ecuación lineal de primer orden en u′ podemos resolverla para u′ mediante la variación de parámetros como en la Sección 9.2.1, integre la solución para obtener u, y luego obtener y de (9.5.6.3).
Ejemplo ilustrativo 9.5.6_1
(a) Encuentre la solución general de la ecuación
(9.5.6.6)
dado que y1 = ex es una solución de la ecuación complementaria
(9.5.6.7)
(b) Como subproducto de (a), encuentre un conjunto fundamental de soluciones de (9.5.6.7).
Solución:
(a)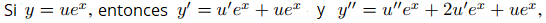 
de tal modo que
Por lo tanto y = uex es una solución de (9.5.6.6) si y solo si
que es una ecuación de primer orden en u′. Lo reescribimos como
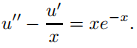(9.5.6.8)
Para centrarnos en cómo aplicamos la variación de parámetros a esta ecuación, escribimos temporalmente z = u′, de modo que (9.5.6.8) se convierte en
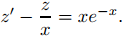(9.5.6.9)
Te dejamos mostrar (por separación de variables) que z1 = x es una solución de la ecuación complementaria
para (9.5.6.9). Al aplicar la variación de parámetros como en la Sección 9.2.1, ahora podemos ver que cada solución de (9.5.6.9) tiene la forma
z = vx
donde
por consiguiente
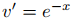y 
Como u′ = z = vx, u es una solución de (9.5.6.8) si y solo si
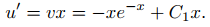
Integrando, se obtiene
Por tanto, la solución general de (9.5.6.6) es
(9.5.6.10)
(b) Dejando C1 = C2 = 0 en (9.5.6.10), vemos que yp1 = x + 1 es una solución de (9.5.6.6). Dejando C1 = 2 y C2 = 0, vemos que yp2 = x + 1 + x2ex también es una solución de (9.5.6.6). Dado que la diferencia de dos soluciones de (9.5.6.6) es una solución de (9.5.6.7), y2 = yp1 − yp2 = x2ex es una solución de (9.5.6.7). Como y2 / y1 no es constante y ya sabemos que y1 = ex es una solución de (9.5.6.6), el teorema 9.5.1.6 implica que {ex, x2ex} es un conjunto fundamental de soluciones de (9.5.6.7). ◊
Aunque (9.5.6.10) es una forma correcta para la solución general de (9.5.6.6), es una tontería dejar el coeficiente arbitrario de x2ex como C1/2 donde C1 es una constante arbitraria. Además, es sensato hacer que los subíndices de los coeficientes de y1 = ex y y2 = x2ex sean consistentes con los subíndices de las funciones mismas. Por lo tanto, reescribimos (9.5.6.10) como
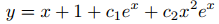
simplemente cambiando el nombre de las constantes arbitrarias. También haremos esto en los dos ejemplos siguientes y en las respuestas a los ejercicios.
Ejemplo ilustrativo 9.5.6_2
(a) Encuentre la solución general de
dado que y1 = x es una solución de la ecuación complementaria
(9.5.6.11)
Como subproducto de este resultado, encuentre un conjunto fundamental de soluciones de (9.5.6.11).
(b) Resuelve el problema de valor inicial
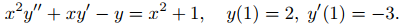(9.5.6.12)
Solución:
(a) Si y = ux, entonces y′ = u′x + u y y″ = u″x + 2u′, de tal modo que
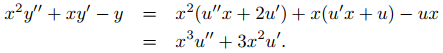
Por lo tanto y = ux es una solución de (9.5.6.12) si y solo si
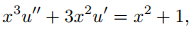
que es una ecuación de primer orden en u′. Lo reescribimos como
(9.5.6.13)
Para centrarnos en cómo aplicamos la variación de parámetros a esta ecuación, escribimos temporalmente z = u′, de modo que (9.5.6.13) se convierta en
(9.5.6.14)
Te dejamos mostrar por separación de variables que z1 = 1/x3 es una solución de la ecuación complementaria
para (9.5.6.14). Por variación de parámetros, toda solución de (9.5.6.14) tiene la forma
dónde
entonces
Como u′ = z = v/x3, u es una solución de (9.5.6.14) si y solo si
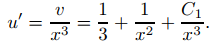
Integrando, se obtiene
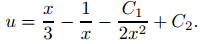
Por tanto, la solución general de (9.5.6.12) es
(9.5.6.15)
Razonando como en la solución del ejemplo 9.5.6.1 (a), concluimos que y1 = x y y2 = 1/x forman un conjunto fundamental de soluciones para (9.5.6.11).
Como explicamos anteriormente, cambiamos el nombre de las constantes en (9.5.6.15) y las reescribimos como
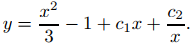(9.5.6.16)
(b) Diferenciando (9.5.6.16) obtenemos
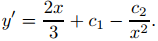(9.5.6.17)
Estableciendo x = 1 en (9.5.6.16) y (9.5.6.17) e imponiendo las condiciones iniciales y(1) = 2 y y′(1) = −3 produce
Resolver estas ecuaciones produce c1 = −1/2, c2 = 19/6. Por lo tanto, la solución de (9.5.6.12) es
◊
El uso de la reducción de orden para encontrar la solución general de una ecuación lineal homogénea de segundo orden conduce a una ecuación lineal homogénea de primer orden en u′ que puede resolverse mediante la separación de variables. El siguiente ejemplo ilustra esto.
Ejemplo ilustrativo 9.5.6_3
Encuentre la solución general y un conjunto fundamental de soluciones de
(9.5.6.18)
dado que y1 = x es una solución.
Solución:
Si y = ux entonces y′ = u′x + u y y″ = u″x + 2u′, de tal modo que
Por lo tanto y = ux es una solución de (9.5.6.18) si y solo si
Separando las variables u y x se obtiene
entonces
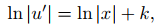o equivalente, 
Por lo tanto
entonces la solución general de (9.5.6.18) es
La que reescribimos como
Por lo tanto, {x, x3} es un conjunto fundamental de soluciones de (9.5.6.18). ♦