| 9. Ecuaciones diferenciales | 9.3. Métodos numéricos | 9.3.1. Método de Euler |
Ejercicios propuestos para el Capítulo 9.3.1
Es posible que desee guardar los resultados de estos ejercicios, ya que los revisaremos en las próximas dos secciones. En los ejercicios 1 a 5, use el método de Euler para encontrar valores aproximados de la solución del problema de valor inicial dado en los puntos xi = x0 + ih, donde x0 es el punto donde se impone la condición inicial e i = 1, 2, 3. El propósito de estos ejercicios es familiarizarlo con el procedimiento computacional del método de Euler.
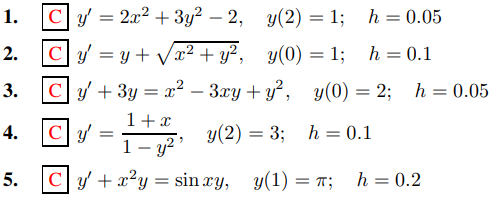
6. C Usar el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 para encontrar valores aproximados de la solución del problema de valor inicial
y′ + 3y = 7e4x, y(0) = 2
en x = 0, 0.1, 0.2, 0.3, . . . , 1.0. Compare estos valores aproximados con los valores de la solución exacta y = e4x + e−3x, que puede obtenerse por el método de la Sección 9.2.1. Presente sus resultados en una tabla como la Tabla 9.3.1.1.
7. C Usar el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 para encontrar valores aproximados de la solución del problema de valor inicial
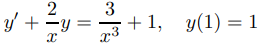
en x = 1,0, 1,1, 1,2, 1,3, . . . , 2.0. Compare estos valores aproximados con los valores de la solución exacta
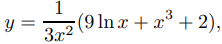
que se puede obtener por el método de la Sección 9.2.1. Presente sus resultados en una tabla como la Tabla 9.3.1.1.
8. C Usar el método de Euler con tamaños de paso h = 0.05, h = 0.025 y h = 0.0125 para encontrar valores aproximados de la solución del problema de valor inicial
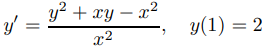
en x = 1,0, 1,05, 1,10, 1,15, . . . , 1.5. Compare estos valores aproximados con los valores de la solución exacta
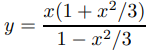
obtenido en el Ejemplo 9.2.4.3. Presente sus resultados en una tabla como la Tabla 9.3.1.1.
9. C En el Ejemplo 9.2.2.3 se demostró que
y5 + y = x2 + x − 4
es una solución implícita del problema de valor inicial

Use el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 para encontrar valores aproximados de la solución de (A) en x = 2.0, 2.1, 2.2, 2.3, . . . , 3.0. Presente sus resultados en forma tabular. Para verificar el error en estos valores aproximados, construya otra tabla de valores del residual
R(x, y) = y5 + y − x2 − x + 4
para cada valor de (x, y) que aparece en la primera tabla.
10. C Puedes ver en el Ejemplo 9.2.5.1 que
x4y3 + x2y5 + 2xy = 4
es una solución implícita del problema de valor inicial
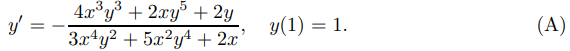
Use el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 para encontrar valores aproximados de la solución de (A) en x = 1.0, 1.1, 1.2, 1.3, . . . , 2.0. Presente sus resultados en forma tabular. Para verificar el error en estos valores aproximados, construya otra tabla de valores del residual
R(x, y) = x4y3 + x2y5 + 2xy − 4
para cada valor de (x, y) que aparece en la primera tabla.
11. C Usar el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 para encontrar valores aproximados de la solución del problema de valor inicial
(3y2 + 4y)y′ + 2x + cosx = 0, y(0) = 1; (Ejercicio 9.2.2.13)
en x = 0, 0.1, 0.2, 0.3, . . . , 1.0.
12. C Usar el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 para encontrar valores aproximados de la solución del problema de valor inicial
en x = 1,0, 1,1, 1,2, 1,3, . . . , 2.0.
13. C Usar el método de Euler y el método semilineal de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 para encontrar valores aproximados de la solución del problema de valor inicial
y′ + 3y = 7e−3x, y(0) = 6
en x = 0, 0.1, 0.2, 0.3, . . . , 1.0. Compare estos valores aproximados con los valores de la solución exacta y = e−3x(7x + 6), que puede obtenerse por el método de la Sección 9.2.1. ¿Notas algo especial en los resultados? Explique.
Los problemas de valores iniciales lineales de los ejercicios 14 a 19 no se pueden resolver exactamente en términos de funciones elementales conocidas. En cada ejercicio, use el método de Euler y los métodos semilineales de Euler con los tamaños de paso indicados para encontrar valores aproximados de la solución del problema de valor inicial dado en 11 puntos equidistantes (incluidos los puntos finales) en el intervalo.

En los ejercicios 20 a 22, use el método de Euler y el método semilineal de Euler con los tamaños de paso indicados para encontrar valores aproximados de la solución del problema de valor inicial dado en 11 puntos equidistantes (incluidos los puntos finales) en el intervalo.
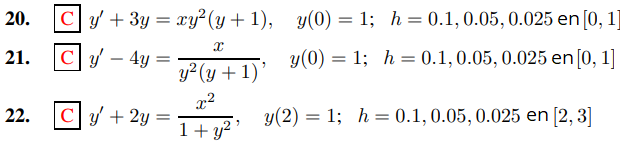
23. CUADRATURA NUMÉRICA. El teorema fundamental del cálculo dice que si f es continua en un intervalo cerrado [a, b] entonces tiene una antiderivada F tal que F′(x) = f(x) en [a, b] y
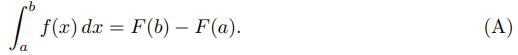
Esto resuelve el problema de evaluar una integral definida si el integrando f tiene una antiderivada que se puede encontrar y evaluar fácilmente. Sin embargo, si f no tiene esta propiedad, (A) no proporciona una forma útil de evaluar la integral definida. En este caso debemos recurrir a métodos aproximados. Hay una clase de tales métodos llamada cuadratura numérica, donde la aproximación toma la forma
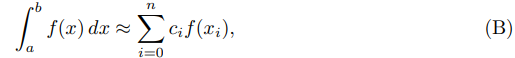
donde a = x0 < x1 < · · · < xn = b son puntos adecuadamente elegidos y c0, c1, . . . , cn son constantes adecuadamente elegidas. Llamamos (B) una fórmula de cuadratura.
(a) Deduzca la fórmula de cuadratura

aplicando el método de Euler al problema de valor inicial
y′ = f(x), y(a) = 0.
(b) La fórmula de cuadratura (C) a veces se denomina regla del rectángulo izquierdo. Dibuja una figura que justifique esta terminología.
(c) L Para varias opciones de a, b y A, aplique (C) a f(x) = A con n = 10, 20, 40, 80, 160, 320. Compare sus resultados con las respuestas exactas y explique lo que encuentras.
(d) L Para varias opciones de a, b, A y B, aplique (C) a f(x) = A + Bx con n = 10, 20, 40, 80, 160, 320. Compare sus resultados con las respuestas exactas y explique lo que encuentre.
9.3.2 El método de Euler mejorado y métodos relacionados »

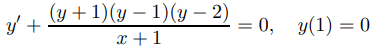 (
(