| 9. Ecuaciones diferenciales | 9.10. Sistemas lineales de ecuaciones diferenciales | Ejercicios propuestos para el Capítulo 9.10.6 |
9.10.6 Sistemas homogéneos con coeficientes constantes III
Ahora consideramos el sistema y′ = Ay, donde A tiene un valor propio complejo λ = α + iβ con β ≠ 0 Seguimos suponiendo que A tiene entradas reales, por lo que el polinomio característico de A tiene coeficientes reales. Esto implica que λ = α − iβ también es un valor propio de A.
Un vector propio x de A asociado con λ = α + iβ tendrá entradas complejas, por lo que escribiremos
x = u + iv
donde u y v tienen entradas reales; es decir, u y v son las partes real e imaginaria de x. Como Ax = λx,
A(u + iv) = (α + iβ)(u + iv). (9.10.6.1)
Tomando conjugados complejos aquí y recordando que A tiene entradas reales produce
A(u − iv) = (α − iβ)(u − iv),
lo que muestra que x = u − iv es un vector propio asociado con 
= α − iβ. Los valores propios complejos conjugados λ y pueden asociarse por separado con soluciones linealmente independientes y′ = Ay; sin embargo, no seguiremos este enfoque, ya que las soluciones obtenidas de esta manera resultan ser de valor complejo. En cambio, obtendremos soluciones de y′ = Ay en la forma
y = f1u + f2v (9.10.6.2)
donde f1 y f2 son funciones escalares de valor real. El siguiente teorema muestra cómo hacer esto.
Teorema 9.10.6.1
Sea A una matriz n × n con entradas reales. Sea λ = α + iβ (β ≠ 0) un valor propio complejo de A y sea x = u + iv un vector propio asociado, donde u y v tienen componentes reales. Entonces u y v son distintos de cero y
y1 = eαt(u cosβt − v sen βt) y y2 = eαt(u senβt + v cosβt),
que son las partes real e imaginaria de
eαt(cosβt + i sen βt)(u + iv), (9.10.6.3)
son soluciones linealmente independientes de y′ = Ay. ♦
Demostración:
Una función de la forma (9.10.6.2) es una solución de y′ = Ay si y solo si
(9.10.6.4)
Realizando la multiplicación indicada en el lado derecho de (9.10.6.1) y reuniendo las partes real e imaginaria del resultado se obtiene
A(u + iv) = (αu − βv) + i(αv + βu).
Igualando las partes real e imaginaria en los dos lados de esta ecuación se obtiene
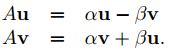
Le dejamos a usted (Ejercicio 25) demostrar a partir de esto que tanto u como v son distintos de cero. Sustituyendo estas ecuaciones en (9.10.6.4) se obtiene
Esto es cierto si
o, de manera equivalente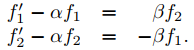 
Si hacemos que f1 = g1eαt y f2 = g2eαt, donde se determinarán g1 y g2, entonces las dos últimas ecuaciones se convierten en
lo que implica que
por lo que
La solución general de esta ecuación es
g1 = c1 cosβt + c2 senβt.
Además, dado que g2 = g1′/β,
g2 = −c1 senβt + c2 cosβt.
Multiplicando g1 y g2 por eαt se muestra que
Sustituyendo estas funciones en (910.6.2) muestra que
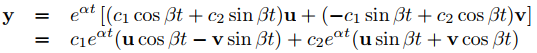(9.10.6.5)
es una solución de y′ = Ay para cualquier elección de las constantes c1 y c2. En particular, tomando primero c1 = 1 y c2 = 0 y luego c1 = 0 y c2 = 1, vemos que y1 e y2 son soluciones de y′ = Ay. Te dejamos comprobar que son, respectivamente, las partes real e imaginaria de (9.10.6.3) (Ejercicio 26), y que son linealmente independientes (Ejercicio 27). ♦
Ejemplo ilustrativo 9.10.6.1
Encuentre la solución general de
(9.10.6.6)
Solución:
El polinomio característico de la matriz de coeficientes A en (9.10.6.6) es
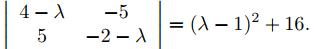
Por lo tanto, λ = 1 + 4i es un valor propio de A. Los vectores propios asociados satisfacen (A − (1 + 4i)I) x = 0.
La matriz aumentada de este sistema es
que es equivalente por filas a
Por lo tanto x1 = (3 + 4i)x2/5. Tomando x2 = 5 se obtiene x1 = 3 + 4i, entonces
es un vector propio. Las partes real e imaginaria de
con
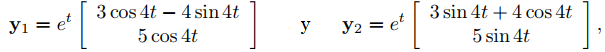
que son soluciones linealmente independientes de (9.10.6.6). La solución general de (9.10.6.6) es
♦
Ejemplo ilustrativo 9.10.6.2
Encuentre la solución general de
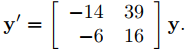(9.10.6.7)
Solución:
El polinomio característico de la matriz de coeficientes A en (9.10.6.7) es
Por lo tanto, λ = 1 + 3i es un valor propio de A. Los vectores propios asociados satisfacen (A − (1 + 3i)I) x = 0.
La matriz aumentada aumentada de este sistema es
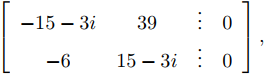
que es equivalente por filas a
Por lo tanto x1 = (5 − i)/2. Tomando x2 = 2 se obtiene x1 = 5 − i, entonces
es un vector propio. Las partes real e imaginaria de
con
que son soluciones linealmente independientes de (9.10.6.7). La solución general de (9.10.6.7) es
♦
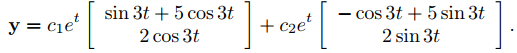Ejemplo ilustrativo 9.10.6.3
Encuentre la solución general de
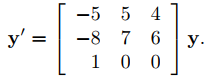(9.10.6.8)
Solución:
El polinomio característico de la matriz de coeficientes A en (9.10.6.8) es
Por lo tanto, los valores propios de A son λ1 = 2, λ2 = i y λ3 = −i. La matriz aumentada de (A − 2I)x = 0 es
que es equivalente por filas a
Por lo tanto x1 = x2 = 2x3. Tomando x3 = 1, se obtiene
así que
es una solución de (9.10.6.8).
La matriz aumentada de (A − iI)x = 0 es
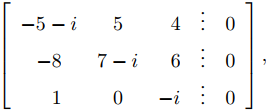
que es equivalente por filas a
.
Por lo tanto x1 = ix3 y x2 = −(1 − i)x3. Tomando x3 = 1 se obtiene el vector propio
Las partes real e imaginaria de
con
que son soluciones de (9.10.6.8). Dado que el Wronskiano de {y1, y2, y3} en t = 0 es
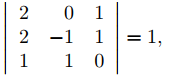
{y1, y2, y3} es un conjunto fundamental de soluciones de (9.10.6.8). La solución general de (9.10.6.8) es
♦
Ejemplo ilustrativo 9.10.6.4
Encuentre la solución general de
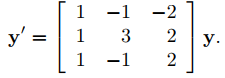(9.10.6.9)
Solución:
El polinomio característico de la matriz de coeficientes A en (9.10.6.9) es
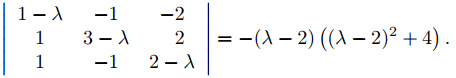
Por lo tanto, los valores propios de A son λ1 = 2, λ2 = 2 + 2i y λ3 = 2 − 2i. La matriz aumentada de (A − 2I)x = 0 es
que es equivalente por filas a
Por lo tanto x1 = x2 = −x3. Tomando x3 = 1, se obtiene
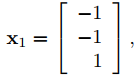
por lo que
es una solución de (9.10.6.9).
La matriz aumentada de (A − (2 + 2i)I) x = 0 es
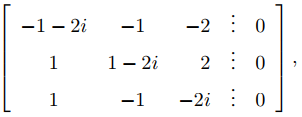
que es equivalente por filas a
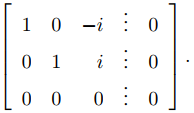
Por lo tanto x1 = ix3 y x2 = −ix3. Tomando x3 = 1 se obtiene el vector propio
Las partes real e imaginaria de
son
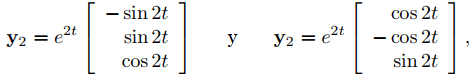
que son soluciones de (9.10.6.9). Dado que el Wronskiano de {y1, y2, y3} en t = 0 es
{y1, y2, y3}} es un conjunto fundamental de soluciones de (9.10.6.9). La solución general de (9.10.6.9) es
♦
Propiedades geométricas de soluciones cuando n = 2
Ahora consideraremos las propiedades geométricas de las soluciones de un sistema de coeficientes constantes de 2 × 2
(9.10.6.10)
bajo los supuestos de esta sección; es decir, cuando la matriz
tiene un valor propio complejo λ = α + iβ (β ≠ 0) y x = u + iv es un vector propio asociado, donde u y v tienen componentes reales. Para describir las trayectorias con precisión es necesario introducir un nuevo sistema de coordenadas rectangulares en el plano y1–y2. Esto plantea un punto que no había surgido antes: siempre es posible elegir x de modo que (u, v) = 0. Se requiere un esfuerzo especial para hacer esto, ya que no todos los vectores propios tienen esta propiedad. Sin embargo, si conocemos un vector propio que no lo hace, podemos multiplicarlo por una constante compleja adecuada para obtener uno que sí lo haga. Para ver esto, tenga en cuenta que si x es un vector propio λ de A y k es un número real arbitrario, entonces
x1 = (1 + ik)x = (1 + ik)(u + iv) = (u − kv) + i(v + ku)
es también un λ-eigenvector de A, ya que
Ax1 = A((1 + ik)x) = (1 + ik)Ax = (1 + ik)λx = λ((1 + ik)x) = λx1.
Las partes real e imaginaria de x1 son
u1 = u − kv y v1 = v + ku, (9.10.6.11)
Por lo que
Por lo tanto (u1, v1) = 0 si
(u, v)k2 + (||v||2 − ||u||2)k − (u, v) = 0. (9.10.6.12)
Si (u, v) ≠ 0 podemos usar la fórmula cuadrática para encontrar dos valores reales de k tales que (u1, v1) = 0 = 0 (Ejercicio 28).
Ejemplo ilustrativo 9.10.6.5
En el ejemplo 9.10.6.1 encontramos el vector propio
para la matriz del sistema (9.10.6.6). Aquí 
y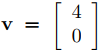 
no son ortogonales, ya que (u, v) = 12. Como ||v||2 − ||u||2 = −18, (9.10.6.12) es equivalente a
2k2 − 3k − 2 = 0.
Los ceros de esta ecuación son k1 = 2 y k2 = −1/2. Haciendo k = 2 en (9.10.6.11), se obtiene
y (u1, v1) = 0. Haciendo k = −1/2 en (9.10.6.11) se obtiene
y de nuevo (u1, v1) = 0. ♦
(Los números no siempre resultan tan bien como en este ejemplo. Necesitará una calculadora o una computadora para hacer los ejercicios 29 a 40).
De ahora en adelante, supondremos que (u, v) = 0. Sean U y V vectores unitarios en las direcciones de u y v, respectivamente; es decir, U = u/||u|| y V = v/||v||. El nuevo sistema de coordenadas rectangulares tendrá el mismo origen que el sistema y1–y2. Las coordenadas de un punto en este sistema se denotarán por (z1, z2), donde z1 y z2 son los desplazamientos en las direcciones de U y V, respectivamente.
De (9.10.6.5), las soluciones de (9.10.6.10) vienen dadas por
(9.10.6.13)
Por conveniencia, llamemos a la curva atravesada por e−αty(t) una trayectoria de sombra de (9.10.6.10). Multiplicando (9.10.6.13) por e−αt se obtiene
donde
Por lo tanto
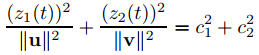
(¡compruébalo!), lo que significa que las trayectorias de sombra de (9.10.6.10) son elipses centradas en el origen, con ejes de simetría paralelos a U y V. Como
el vector desde el origen hasta un punto en la elipse de la sombra gira en la misma dirección en que V tendría que girarse π/2 radianes para que coincida con U (Figuras 9.10.6.1 y 9.10.6.2).
|
Figura 9.10.6.1 Trayectorias de sombra recorridas en el sentido de las agujas del reloj |
Figura 9.10.6.2 Trayectorias de sombra recorridas en sentido antihorario |
Si α = 0, entonces cualquier trayectoria de (9.10.6.10) es una trayectoria de sombra de (9.10.6.10); por lo tanto, si λ es puramente imaginario, entonces las trayectorias de (9.10.6.10) son elipses recorridas periódicamente como se indica en las Figuras 9.10.6.1 y 9.10.6.2.
Si α > 0, entonces
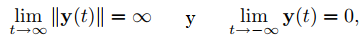
por lo que la trayectoria se aleja del origen cuando t varía de −∞ a ∞. La dirección de la espiral depende de la orientación relativa de U y V, como se muestra en las Figuras 9.10.6.3 y 9.10.6.4
|
Figura 9.10.6.3 α > 0; trayectoria de sombra en espiral hacia afuera |
Figura 9.10.6.4 α > 0; trayectoria de sombra en espiral hacia afuera |
Si α < 0, entonces
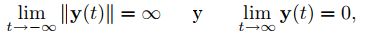
por lo que la trayectoria gira en espiral hacia el origen cuando t varía de −∞ a ∞. Nuevamente, la dirección de la espiral depende de la orientación relativa de U y V, como se muestra en las Figuras 9.10.6.5 y 9.10.6.6.
|
Figura 9.10.6.5 α < 0; trayectoria de sombra en espiral |
Figura 9.10.6.6 α < 0; trayectoria de sombra en espiral hacia adentro |
