| 9. Ecuaciones diferenciales | 9.10. Sistemas lineales de ecuaciones diferenciales | Ejercicios propuestos para el Capítulo 9.10.2 |
9.10.2 SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES
Un sistema de ecuaciones diferenciales de primer orden que se puede escribir en la forma
se llama sistema lineal.
El sistema lineal (9.10.2.1) se puede escribir en forma de matriz como
o más brevemente como
y′ = A(t) y + f (t), (9.10.2.2)
donde
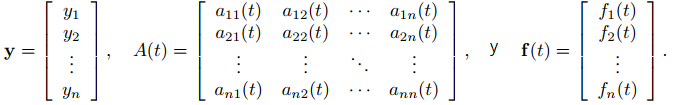
Llamamos A la matriz de coeficientes de (9.10.2.2) y f la función de forzamiento. Diremos que A y f son continuas si sus entradas son continuas. Si f = 0, entonces (9.10.2.2) es homogéneo; de lo contrario, (9.10.2.2) es no homogéneo.
Un problema de valor inicial para (9.10.2.2) consiste en encontrar una solución de (9.10.2.2) que sea igual a un vector constante dado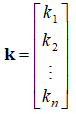
en algún punto inicial t0. Escribimos este problema de valor inicial como
El siguiente teorema proporciona condiciones suficientes para la existencia de soluciones de problemas con valores iniciales para (9.10.2.2). Omitimos la prueba.
Teorema 9.10.2.1
Suponga que la matriz de coeficientes A y la función de forzamiento f son continuas en un intervalo abierto (a, b), sea t0 un valor en (a, b), y sea k un n-vector constante arbitrario. Entonces el problema del valor inicial
tiene una solución única en (a, b). ♦
Ejemplo ilustrativo 9.10.2_1
(a) Escriba el sistema
en forma de matriz y concluya del teorema 9.10.2.1 que todo problema de valor inicial para (9.10.2.3) tiene una solución única en (−∞, ∞).
(b) Verifique que
es una solución de (9.10.2.3) para todos los valores de las constantes c1 y c2.
(c) Encuentre la solución del problema de valor inicial
Solución:
(a) El sistema (9.10.2.3) se puede escribir en forma de matriz como
Un problema de valor inicial para (9.10.2.3) se puede escribir como
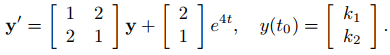
Dado que la matriz de coeficientes y la función de forzamiento son ambas continuas en (−∞, ∞), el teorema 9.10.2.1 implica que este problema tiene una solución única en (−∞, ∞).
(b) Si y está dado por (9.10.2.4), entonces
(c) Debemos elegir c1 y c2 en (9.10.2.4) para que
que es equivalente a
Resolver este sistema produce c1 = 1, c2 = −2, entonces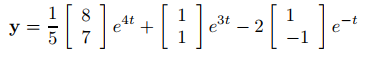
es la solución de (9.10.2.5). ♦
OBSERVACIÓN: La teoría de n × n sistemas lineales de ecuaciones diferenciales es análoga a la teoría de la ecuación escalar de n-ésimo orden
P0(t) y(n) + P1(t) y(n − 1) + · · · + Pn(t) y = F(t), (9.10.2.6)
como se desarrolla en las Secciones 9.9.1. Por ejemplo, reescribiendo (9.10.2.6) como un sistema lineal equivalente se puede demostrar que el teorema 9.10.2.1 implica el teorema 9.9.1.1 (ejercicio 12).