| 9. Ecuaciones diferenciales | 9.11. Problemas de valores en la frontera y expansiones de Fourier | Ejercicios propuestos para el Capítulo 9.11.3 |
9.11.3 Expansiones de Fourier II
En esta sección analizamos las expansiones de Fourier en términos de las funciones propias de los problemas 1 a 4 de la Sección 9.11.1.
Serie del coseno de Fourier
Del Ejercicio 9.11.1.20, las funciones propias

del problema de valor en la frontera
y′′ + λy = 0, y′(0) = 0, y′(L) = 0 (9.11.3.1)
(Problema 2) son ortogonales en [0, L]. Si f es integrable en [0, L], entonces la expansión de Fourier de f en términos de estas funciones se denomina serie de coseno de Fourier de f en [0, L]. Esta serie es
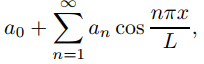
donde
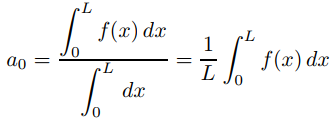 y
y
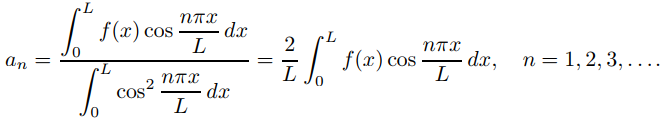
La comparación de esta definición con el Teorema 6(a) muestra que la serie de coseno de Fourier de f en [0, L] es la serie de Fourier de la función
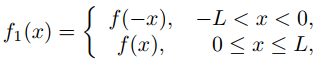
obtenida extendiendo f sobre [−L, L] como una función par (Figura 9.11.3.1).
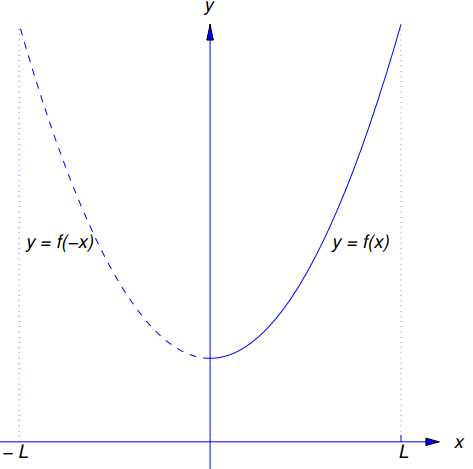
Aplicando el Teorema 9.11.2.2 a f1 se obtiene el siguiente teorema.
Teorema 9.11.3.1
Si f es suave por partes en [0, L], entonces la serie de coseno de Fourier
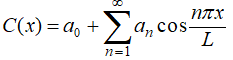
de f en [0, L], con

converge para todo x en [0, L]; además,

Ejemplo ilustrativo 9.11.3.1
Encuentre la serie de coseno de Fourier de f (x) = x en [0, L].
Solución:
Los coeficientes son

y, si n ≥ 1

Por lo tanto
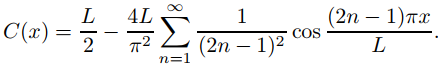
El teorema 9.11.3.1 implica que
C(x) = x, 0 ≤ x ≤ L. ♦
Serie del seno de Fourier
Del Ejercicio 9.11.1.19, las funciones propias

del problema de valor en la frontera
y′′ + λy = 0, y(0) = 0, y(L) = 0 (9.11.3.2)
(Problema 1) son ortogonales en [0, L]. Si f es integrable en [0, L], entonces la expansión de Fourier de f en términos de estas funciones se denomina serie de seno de Fourier de f en [0, L]. esta serie es
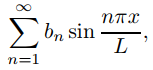
donde

La comparación de esta definición con el Teorema 6(b) muestra que la serie de seno de Fourier de f en [0, L] es la serie de Fourier de la función

obtenido extendiendo f sobre [−L, L] como una función impar (Figura 9.11.3.2).

Aplicando el Teorema 9.11.2.2 a f2 se obtiene el siguiente teorema.
Teorema 9.11.3.2
Si f es suave por partes en [0, L], entonces la serie de seno de Fourier

de f en [0, L], con

converge para todo x en [0, L]; además,

Ejemplo ilustrativo 9.11.3.2
Encuentre la serie de senos de Fourier de f (x) = x en [0, L].
Solución:
Los coeficientes son

Por lo tanto

El teorema 9.11.3.2 implica que
 ♦
♦
Serie mixta de coseno de Fourier
Del Ejercicio 9.11.1.22, las funciones propias

del problema de valor en la frontera
y′′ + λy = 0, y′(0) = 0, y(L) = 0 (9.11.3.2)
(Problema 4) son ortogonales en [0, L]. Si f es integrable en [0, L], entonces la expansión de Fourier de f en términos de estas funciones es

donde

Llamaremos a esta expansión la serie mixta de coseno de Fourier de f en [0, L], porque las condiciones de contorno de (9.11.3.2) son “mixtas” en el sentido de que requieren que y sea cero en un punto de contorno y que y′ sea igual a cero en el otro. Por el contrario, la serie de coseno de Fourier “ordinaria” está asociada con (9.11.3.1), donde las condiciones de contorno requieren que y′ sea cero en ambos extremos.
Puede demostrarse (Ejercicio 57) que la serie mixta de cosenos de Fourier de f en [0, L] es simplemente la restricción a [0, L] de la serie de cosenos de Fourier de

en [0, 2L] (Figura 9.11.3.3).

Figura 9.11.3.3
La aplicación del teorema 9.11.3.1 con f reemplazada por f3 y L reemplazada por 2L produce el siguiente teorema.
Teorema 9.11.3.3
Si f es suave por partes en [0, L], entonces la serie mixta de cosenos de Fourier
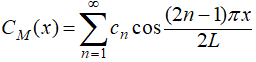
de f en [0, L], con
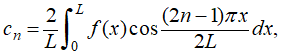
converge para todo x en [0, L]; además,

Ejemplo ilustrativo 9.11.3.3
Encuentre la serie mixta de cosenos de Fourier de f (x) = x − L en [0, L].
Solución:
El coeficiente es

Por lo tanto

El teorema 9.11.3.3 implica que
CM(x) = x − L, 0 ≤ x ≤ L. ♦
Serie mixta de seno de Fourier
Del Ejercicio 9.11.1.21, las funciones propias

del problema de valor en la frontera
y′′ + λy = 0, y(0) = 0, y′(L) = 0
(Problema 3) son ortogonales en [0, L]. Si f es integrable en [0, L], entonces la expansión de Fourier de f en términos de estas funciones es

donde

Llamaremos a esta expansión la serie mixta de senos de Fourier de f en [0, L].
Se puede demostrar (Ejercicio 58) que la serie mixta de senos de Fourier de f en [0, L] es simplemente la restricción a [0, L] de la serie de senos de Fourier de

en [0, 2L] (Figura 9.11.3.4).

Aplicando el Teorema 9.11.3.2 con f reemplazada por f4 y L reemplazada por 2L se obtiene el siguiente teorema.
Teorema 9.11.3.4
Si f es suave por partes en [0, L], entonces la serie mixta de senos de Fourier

de f en [0, L], con

converge para todo x en [0, L]; además,
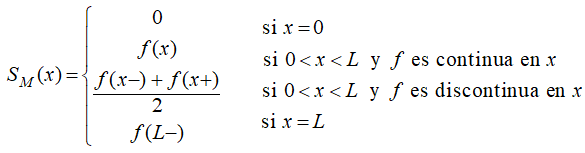 ♦
♦
Ejemplo ilustrativo 9.11.3.4
Encuentre la serie mixta de senos de Fourier de f (x) = x en [0, L].
Solución:
Los coeficientes son

Por lo tanto
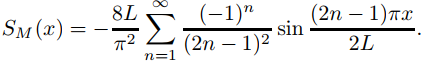
El teorema 9.11.3.4 implica que
SM (x) = x, 0 ≤ x ≤ L. ♦
Una observación útil
En aplicaciones que involucran expansiones en términos de las funciones propias de los Problema 1 a 4, las funciones que se expanden suelen ser polinomios que satisfacen las condiciones de contorno del problema que se está considerando. En este caso el siguiente teorema presenta una manera eficiente de obtener los coeficientes en la expansión.
Teorema 9.11.3.5
(a) Si f ′(0) = f ′(L) = 0, f ′′ es continua y f ′′′ es continua por tramos en [0, L], entonces
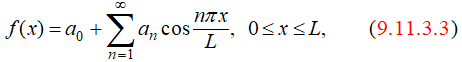
con

Ahora suponga que f ′ es continua y f ′′ es continua por partes en [0, L].
(b) Si f (0) = f (L) = 0, entonces
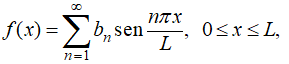
con

(c) Si f ′(0) = f (L) = 0, entonces
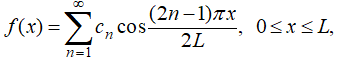
con

(d) Si f (0) = f ′(L) = 0, entonces
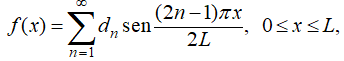
con
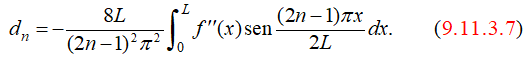
♦
Demostración:
Demostraremos (a) y le dejaremos el resto a usted (Ejercicios 35, 42 y 50). Como f es continua en [0, L], el Teorema 9.11.3.1 implica (9.11.3.3) con a0, a1, a2,… como se define en el Teorema 9.11.3.1. Ya sabemos que a0 es como en (9.11.3.4). Si n ≥ 1, integrando dos veces por partes se obtiene

(Por un argumento similar al utilizado en la demostración del Teorema 9.8.3.1, la última integración por partes es legítima en el caso de que f ′′′ no esté definida en un número finito de puntos en [0, L], siempre que sea por partes continua en [0, L].) Esto completa la prueba. ◊
Ejemplo ilustrativo 9.11.3.5
Encuentre la expansión del coseno de Fourier de f (x) = x2(3L − 2x) en [0, L].
Solución:
Aquí

y

Evaluar esta integral directamente es laborioso. Sin embargo, como f ′ (x) = 6Lx − 6x2, vemos que f ′ (0) = f ′ (L) = 0. Como f ′′′(x) = −12, vemos de (9.11.3.4) que si n ≥ 1 entonces

Por lo tanto

♦
Ejemplo ilustrativo 9.11.3.6
Encuentre la expansión del seno de Fourier de f (x) = x(x2 − 3Lx + 2L2) en [0, L].
Solución:
Como f (0) = f (L) = 0 y f ′′(x) = 6(x − L), vemos de (9.11.3.5) que
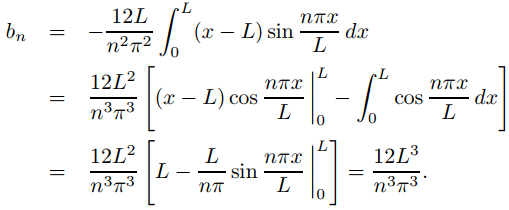
Por lo tanto
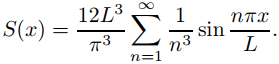
♦
Ejemplo ilustrativo 9.11.3.7
Encuentre la expansión mixta del coseno de Fourier de f (x) = 3x3 − 4Lx2 + L3 en [0, L].
Solución:
Como f ′(0) = f (L) = 0 y f ′′(x) = 2(9x − 4L), vemos de (9.11.3.6) que
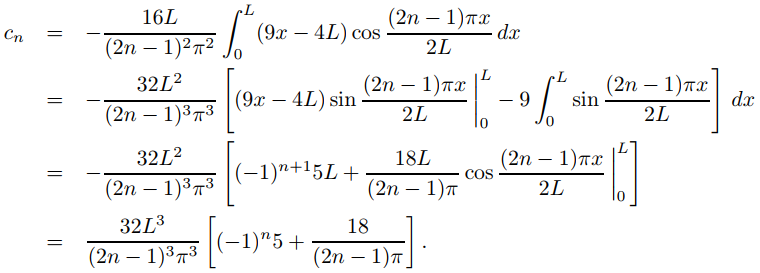
Por lo tanto

♦
Ejemplo ilustrativo 9.11.3.8
Encuentre la expansión del seno de Fourier mixto de f (x) = x(2x2 − 9Lx + 12L2) en [0, L].
Solución:
Como f (0) = f ′(L) = 0, y f ′′(x) = 6(2x − 3L), vemos de (9.11.3.7) que

Por lo tanto

♦

Buenas tardes 😺