| 4. Aplicaciones de la derivada | Ejercicios propuestos para el Capítulo 4.1 |

4.1 TASAS DE VARIACIÓN RELACIONADAS

Objetivos de aprendizaje:

4.1.1 Expresar cantidades cambiantes en términos de derivadas.
4.1.2. Encontrar relaciones entre las derivadas en un problema dado.
4.1.3. Usar la regla de la cadena para encontrar la tasa de cambio de una cantidad que depende de la tasa de cambio de otras cantidades.

      Hemos visto que para las cantidades que cambian con el tiempo, las tasas a las que cambian estas cantidades están dadas por derivadas. Si dos cantidades relacionadas cambian con el tiempo, las tasas a las que cambian las cantidades están relacionadas. Por ejemplo, si un globo se está llenando de aire, tanto el radio del globo como el volumen del globo están aumentando. En esta sección, consideramos varios problemas en los que dos o más cantidades relacionadas están cambiando y estudiamos cómo determinar la relación entre las tasas de cambio de estas cantidades.

Configuración de problemas de tasas de variación relacionadas

En muchas aplicaciones del mundo real, las cantidades relacionadas están cambiando con respecto al tiempo. Por ejemplo, si consideramos nuevamente el ejemplo del globo, podemos decir que la tasa de cambio en el volumen, V, está relacionada con la tasa de cambio en el radio, r. En este caso, decimos que dV/dt y dr/dt son tasas relacionadas porque V está relacionado con r. Aquí estudiamos varios ejemplos de cantidades relacionadas que están cambiando con respecto al tiempo y observamos cómo calcular una tasa de cambio dada otra tasa de cambio.

Ejemplo ilustrativo 4.1.1: “Inflando un globo”

Un globo esférico se está llenando de aire a una tasa constante de 2 cm³/s (Figura 4.1.1). ¿A qué velocidad está aumentando el radio cuando el radio es de 3 cm?

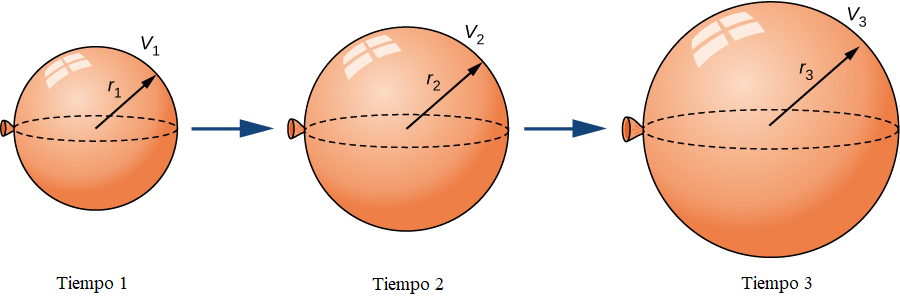
Figura 4.1.1 A medida que el globo se llena de aire, tanto el radio como el volumen aumentan con respecto al tiempo.

Solución:

El volumen de una esfera de radio \(r\) centímetros es

\[ V = \frac{4}{3}\pi r^3 \, \text{cm}^3. \]

Dado que el globo se está llenando con aire, tanto el volumen como el radio son funciones del tiempo. Por lo tanto, \(t\) segundos después de comenzar a llenar el globo con aire, el volumen de aire en el globo es

\[ V(t) = \frac{4}{3}\pi [r(t)]^3 \, \text{cm}^3. \]

Diferenciando ambos lados de esta ecuación con respecto al tiempo y aplicando la regla de la cadena, vemos que la tasa de cambio en el volumen está relacionada con la tasa de cambio en el radio por la ecuación

\[ V'(t) = 4\pi [r(t)]^2 r'(t). \]

El globo se está llenando con aire a una tasa constante de \(2 \, \text{cm}^3/\text{s}\), por lo que \(V'(t) = 2 \, \text{cm}^3/\text{s}\). Por lo tanto,

\[ 2 \, \text{cm}^3/\text{s} = (4\pi [r(t)]^2 \, \text{cm}^2) \cdot (r'(t) \, \text{cm}/\text{s}), \]

lo que implica

\[ r'(t) = \frac{1}{2\pi [r(t)]^2} \, \text{cm}/\text{s}. \]

Cuando el radio \(r = 3 \, \text{cm}\),

\[ r'(t) = \frac{1}{18\pi} \, \text{cm}/\text{s}. \]

♦

Ejercicio de control 4.1.1

¿Cuál es la tasa de cambio instantánea del radio cuando r = 6 cm? ♦ 

      A continuación, describimos la estrategia de resolución de problemas que usaremos para resolver problemas de tasas relacionadas.

Estrategia de resolución de problemas: resolver un problema de tasas de variación relacionadas

1. Asigne símbolos a todas las variables involucradas en el problema. Dibuje una figura si corresponde.
2. Indique, en términos de las variables, la información que se proporciona y la tasa a determinar.
3. Encuentre una ecuación que relacione las variables introducidas en el paso 1.
4. Usando la regla de la cadena, diferencie ambos lados de la ecuación que se encuentra en el paso 3 con respecto a la variable independiente. Esta nueva ecuación relacionará las derivadas.
5. Sustituya todos los valores conocidos en la ecuación del paso 4, luego resuelva la tasa de cambio desconocida.

♦

      Tenga en cuenta que al resolver un problema de tasas relacionadas, es crucial no sustituir los valores conocidos demasiado pronto. Por ejemplo, si el valor de una cantidad cambiante se sustituye en una ecuación antes de que ambos lados de la ecuación se diferencien, entonces esa cantidad se comportará como una constante y su derivada no aparecerá en la nueva ecuación encontrada en el paso 4. 

Ilustraciones del proceso

Ahora implementemos la estrategia recién descrita para resolver varios problemas de tasas relacionadas. El primer ejemplo involucra un avión volando sobre nuestras cabezas. La relación que estamos estudiando es entre la velocidad del avión y la tasa a la que cambia la distancia entre el avión y una persona en el suelo.

Ejemplo ilustrativo 4.1.2: “Un Avión Volando a una Elevación Constante”

Un avión vuela sobre nuestras cabezas a una elevación constante de 4000 pies. Un hombre está observando el avión desde una posición a 3000 pies de la base de una torre de radio. El avión vuela horizontalmente alejándose del hombre. Si el avión vuela ¹ a una velocidad de 600 pies/segundo, ¿a qué velocidad aumenta la distancia entre el hombre y el avión cuando el avión pasa por encima de la torre de radio?

Solución:

Paso 1. Dibuje un diagrama, introduciendo variables para representar las diferentes cantidades involucradas.

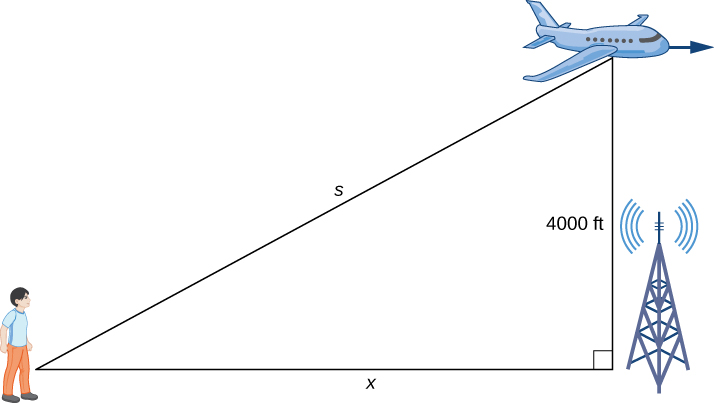
Figura 4.1.2 Un avión está volando a una altura constante de 4000 pies. La distancia entre la persona y el avión y la persona y el punto en el suelo directamente debajo del avión están cambiando. Denotamos esas cantidades con las variables s y x, respectivamente.

Como se muestra, x denota la distancia entre el hombre y la posición en el suelo directamente debajo del avión. La variable s denota la distancia entre el hombre y el ¹ avión. Observe que tanto x como s son funciones del tiempo. No introducimos una variable para la altura del avión porque permanece a una elevación constante de 4000 pies. Dado que la altura de un objeto sobre el suelo se mide como la distancia más corta entre el objeto y el suelo, el segmento de línea de longitud 4000 pies es perpendicular al segmento de línea de longitud x pies, creando un triángulo rectángulo.

Paso 2. Dado que \(x\) denota la distancia horizontal entre el hombre y el punto en el suelo debajo del avión, \(\frac{dx}{dt}\) representa la velocidad del avión. Se nos dice que la velocidad del avión es de 600 pies/seg. Por lo tanto, \(\frac{dx}{dt} = 600\) pies/seg. Como se nos pide que encontremos la tasa de cambio en la distancia entre el hombre y el avión cuando el avión está directamente sobre la torre de radio, necesitamos encontrar \(\frac{ds}{dt}\) cuando \(x = 3000\) pies.

Paso 3. De la figura, podemos usar el teorema de Pitágoras para escribir una ecuación que relaciona \(x\) y \(s\):

\[ [x(t)]^2 + 4000^2 = [s(t)]^2. \]

Paso 4. Diferenciando esta ecuación con respecto al tiempo y usando el hecho de que la derivada de una constante es cero, llegamos a la ecuación

\[ x \frac{dx}{dt} = s \frac{ds}{dt}. \]

Paso 5. Encuentra la tasa a la que la distancia entre el hombre y el avión está aumentando cuando el avión está directamente sobre la torre de radio. Es decir, encuentra \(\frac{ds}{dt}\) cuando \(x = 3000\) pies. Dado que la velocidad del avión es de \(600\) pies/seg, sabemos que

\[ \frac{dx}{dt} = 600 \, \text{pies}/\text{seg}. \]

No se nos da un valor explícito para \(s\); sin embargo, dado que estamos tratando de encontrar \(\frac{ds}{dt}\) cuando \(x = 3000\) pies, podemos usar el teorema de Pitágoras para determinar la distancia \(s\) cuando \(x = 3000\) y la altura es de 4000 pies. Resolviendo la ecuación

\[ 3000^2 + 4000^2 = s^2 \]

para \(s\), tenemos \(s = 5000\) pies en el momento de interés. Usando estos valores, concluimos que \(\frac{ds}{dt}\) es una solución de la ecuación

\[ (3000)(600) = (5000) \cdot \frac{ds}{dt}. \]

Por lo tanto,

\[ \frac{ds}{dt} = \frac{3000 \cdot 600}{5000} = 360 \, \text{pies}/\text{seg}. \]

Nota: Al resolver problemas de tasas relacionadas, es importante no sustituir valores para las variables demasiado pronto. Por ejemplo, en el paso 3, relacionamos las cantidades variables \(x(t)\) y \(s(t)\) mediante la ecuación

\[ {[x(t)]}^2 + 4000^2 = {[s(t)]}^2. \]

Dado que el avión permanece a una altura constante, no es necesario introducir una variable para la altura, y se nos permite usar la constante 4000 para denotar esa cantidad. Sin embargo, las otras dos cantidades están cambiando. Si sustituimos erróneamente \(x(t) = 3000\) en la ecuación antes de diferenciar, nuestra ecuación habría sido

\[ 3000^2 + 4000^2 = [s(t)]^2. \]

Después de diferenciar, nuestra ecuación se convertiría en

\[ 0 = s(t) \frac{ds}{dt}. \]

Como resultado, concluiríamos incorrectamente que \(\frac{ds}{dt} = 0\).

♦

Ejercicio de control 4.1.2

¿Cuál es la velocidad del avión si la distancia entre la persona y el avión está aumentando a una tasa de 300 pies/segundo? ♦

      Ahora volvemos al problema que involucra el lanzamiento del cohete del comienzo del capítulo.

Ejemplo ilustrativo 4.1.3: “Apertura de Capítulo: El Lanzamiento de un Cohete”

Figura 4.1.3

Un cohete es lanzado de manera que se eleva verticalmente. Una cámara está posicionada a 5000 pies del sitio de lanzamiento. Cuando el cohete está a 1000 pies sobre el sitio de lanzamiento, su velocidad es de 600 pies/segundo. Encuentre la tasa de cambio necesaria del ángulo de la cámara en función del tiempo para que se mantenga enfocada en el cohete.

Solución:

Paso 1. Dibuje un diagrama introduciendo las variables:

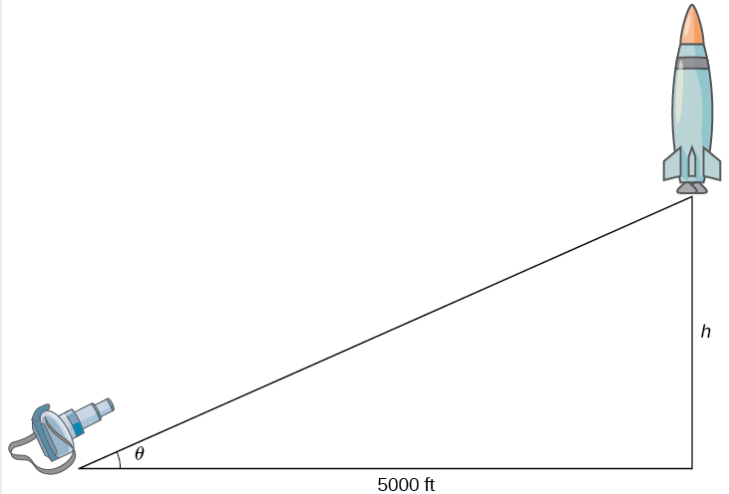
Figura 4.1.4 Una cámara está posicionada a 5000 pies del sitio de lanzamiento del cohete. La altura del cohete y el ángulo de la cámara están cambiando con respecto al tiempo. Denotamos esas cantidades con las variables h y θ, respectivamente.

Sea \(h\) la altura del cohete sobre la plataforma de lanzamiento y \(\theta\) el ángulo entre la lente de la cámara y el suelo.

Paso 2. Estamos tratando de encontrar la tasa de cambio en el ángulo de la cámara con respecto al tiempo cuando el cohete está a 1000 pies del suelo. Es decir, necesitamos encontrar \(\frac{d\theta}{dt}\) cuando \(h = 1000\) pies. En ese momento, sabemos que la velocidad del cohete es \(\frac{dh}{dt} = 600\) pies/seg.

Paso 3. Ahora necesitamos encontrar una ecuación que relacione las dos cantidades que están cambiando con respecto al tiempo: \(h\) y \(\theta\). ¿Cómo podemos crear tal ecuación? Usando el hecho de que hemos dibujado un triángulo rectángulo, es natural pensar en las funciones trigonométricas. Recordemos que \(\tan \theta\) es la razón entre la longitud del lado opuesto del triángulo y la longitud del lado adyacente. Por lo tanto, tenemos

\[ \tan \theta = \frac{h}{5000}. \]

Esto nos da la ecuación

\[ h = 5000 \tan \theta. \]

Paso 4. Diferenciando esta ecuación con respecto al tiempo \(t\), obtenemos

\[ \frac{dh}{dt} = 5000 \sec^2 \theta \frac{d\theta}{dt}. \]

Paso 5. Queremos encontrar \(\frac{d\theta}{dt}\) cuando \(h = 1000\) pies. En este momento, sabemos que \(\frac{dh}{dt} = 600\) pies/seg. Necesitamos determinar \(\sec^2 \theta\). Recordemos que \(\sec \theta\) es la razón entre la longitud de la hipotenusa y la longitud del lado adyacente. Sabemos que la longitud del lado adyacente es de 5000 pies. Para determinar la longitud de la hipotenusa, usamos el teorema de Pitágoras, donde la longitud de un cateto es de 5000 pies, la longitud del otro cateto es \(h = 1000\), y la longitud de la hipotenusa es \(c\) pies, como se muestra en la siguiente figura.

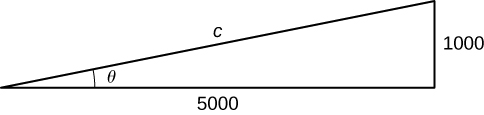
Figura 4.1.5

Vemos que

\[ 1000^2 + 5000^2 = c^2 \]

y concluimos que la hipotenusa es

\[ c = 1000\sqrt{26} \, \text{pies}. \]

Por lo tanto, cuando \(h = 1000\), tenemos

\[ \sec^2 \theta = \left(\frac{1000\sqrt{26}}{5000}\right)^2 = \frac{26}{25}. \]

Recordemos del paso 4 que la ecuación que relaciona \(\frac{d\theta}{dt}\) con nuestros valores conocidos es

\[ \frac{dh}{dt} = 5000 \sec^2 \theta \frac{d\theta}{dt}. \]

Cuando \(h = 1000\) pies, sabemos que \(\frac{dh}{dt} = 600\) pies/seg y \(\sec^2 \theta = \frac{26}{25}\). Sustituyendo estos valores en la ecuación anterior, llegamos a la ecuación

\[ 600 = 5000 \left(\frac{26}{25}\right) \frac{d\theta}{dt}. \]

Por lo tanto,

\[ \frac{d\theta}{dt} = \frac{3}{26} \, \text{rad}/\text{seg}. \]

♦

Ejercicio de control 4.1.3

¿Qué tasa de cambio es necesaria para el ángulo de elevación de la cámara si la cámara se coloca en el suelo a una distancia de 4000 pies del sitio de lanzamiento y la velocidad del cohete es de 500 pies/segundo cuando el cohete está a 2000 pies del suelo? ♦

      En el siguiente ejemplo, consideramos el drenaje de agua de un embudo con forma de cono. Comparamos la velocidad a la que disminuye el nivel del agua en el cono con la velocidad a la que disminuye el volumen del agua.

Ejemplo ilustrativo 4.1.4: “Drenaje de Agua de un Embudo”

El agua está drenando del fondo de un embudo con forma de cono a una velocidad de 0.03 pies cúbicos por segundo. La altura del embudo es de 2 pies y el radio en la parte superior del embudo es de 1 pie. ¿A qué velocidad está cambiando la altura del agua en el embudo cuando la altura del agua es de 1/2 pie?

Solución:

Paso 1. Dibujar un diagrama introduciendo las variables:

Figura 4.1.6 El agua está drenando de un embudo de 2 pies de altura y 1 pie de radio. La altura del agua y el radio del agua están cambiando con el tiempo. Denotamos estas cantidades con las variables h y r, respectivamente.

Sea \(h\) denota la altura del agua en el embudo, \(r\) denota el radio del agua en su superficie, y \(V\) denota el volumen del agua.

Paso 2: Necesitamos determinar \(\frac{dh}{dt}\) cuando \(h = \frac{1}{2}\) pie. Sabemos que \(\frac{dV}{dt} = -0.03 \, \text{pies}^3/\text{seg}\).

Paso 3: El volumen de agua en el cono es

\[ V = \frac{1}{3} \pi r^2 h. \]

De la figura, vemos que tenemos triángulos semejantes. Por lo tanto, la razón de los lados en los dos triángulos es la misma. Por lo tanto, \(\frac{r}{h} = \frac{1}{2}\) o \(r = \frac{h}{2}\). Usando este hecho, la ecuación para el volumen se puede simplificar a

\[ V = \frac{1}{3} \pi \left(\frac{h}{2}\right)^2 h = \frac{\pi}{12} h^3. \]

Paso 4: Aplicando la regla de la cadena al diferenciar ambos lados de esta ecuación con respecto al tiempo \(t\), obtenemos

\[ \frac{dV}{dt} = \frac{\pi}{4} h^2 \frac{dh}{dt}. \]

Paso 5: Queremos encontrar \(\frac{dh}{dt}\) cuando \(h = \frac{1}{2}\) pie. Dado que el agua sale a una tasa de \(0.03 \, \text{pies}^3/\text{seg}\), sabemos que \(\frac{dV}{dt} = -0.03 \, \text{pies}^3/\text{seg}\). Por lo tanto,

\[ -0.03 = \frac{\pi}{4} \left(\frac{1}{2}\right)^2 \frac{dh}{dt}. \] \[ -0.03 = \frac{\pi}{16} \frac{dh}{dt}. \]

lo que implica

De ello se deduce que

\[ \frac{dh}{dt} = -\frac{0.48}{\pi} = -0.153 \, \text{pies}/\text{seg}. \]

♦

Ejercicio de control 4.1.4

¿A qué velocidad está cambiando la altura del agua cuando la altura del agua es de 1/4 de pie? ♦