| 10. Cálculo vectorial – Vectores en el espacio | 10.11 Movimiento en el espacio |
Ejercicios propuestos para el Capítulo 10.11
155. Dado $\mathbf{r}(t) = (3t^2 – 2)\mathbf{i} + (2t – \sin(t))\mathbf{j}$, encuentre la velocidad de una partícula que se mueve a lo largo de esta curva.
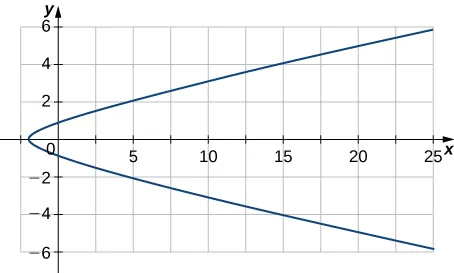
156. Dado $\mathbf{r}(t) = (3t^2 – 2)\mathbf{i} + (2t – \sin(t))\mathbf{j}$, encuentre el vector aceleración de una partícula que se mueve a lo largo de la curva en el ejercicio anterior.
Dadas las siguientes funciones de posición, encuentre la velocidad, la aceleración y la rapidez en términos del parámetro $t$.
157. $\mathbf{r}(t) = \langle 3\cos t, 3\sin t, t^2 \rangle$
158. $\mathbf{r}(t) = e^{-t}\mathbf{i} + t^2\mathbf{j} + \tan t\mathbf{k}$
159. $\mathbf{r}(t) = 2\cos t\mathbf{j} + 3\sin t\mathbf{k}$. La gráfica se muestra aquí:
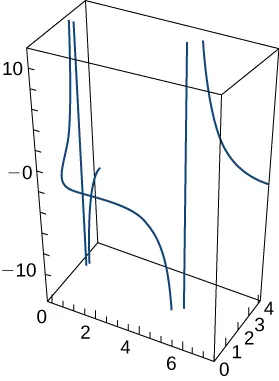
Encuentre la velocidad, aceleración y rapidez de una partícula con la función de posición dada.
160. $\mathbf{r}(t) = \langle t^2 – 1, t \rangle$
161. $\mathbf{r}(t) = \langle e^t, e^{-t} \rangle$. La gráfica se muestra aquí:
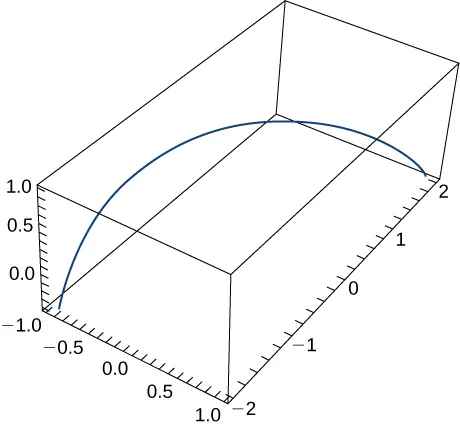
162. $\mathbf{r}(t) = \langle \sin t, t, \cos t \rangle$.
163. La función de posición de un objeto está dada por $\mathbf{r}(t) = \langle t^2, 5t, t^2 – 16t \rangle$. ¿En qué momento la rapidez es mínima?
164. Sea $\mathbf{r}(t) = r\cosh(\omega t)\mathbf{i} + r\sinh(\omega t)\mathbf{j}$. Encuentre los vectores de velocidad y aceleración y demuestre que la aceleración es proporcional a $\mathbf{r}(t)$.
Considere el movimiento de un punto en la circunferencia de un círculo que rueda. A medida que el círculo rueda, genera la cicloide $\mathbf{r}(t) = (\omega t – \sin(\omega t))\mathbf{i} + (1 – \cos(\omega t))\mathbf{j}$, donde $\omega$ es la velocidad angular del círculo:
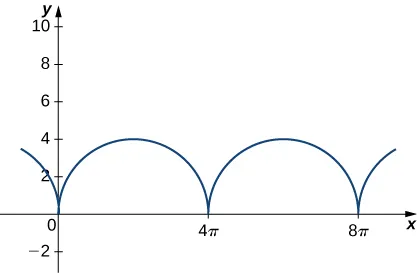
165. Encuentre las ecuaciones para la velocidad, la aceleración y la rapidez de la partícula en cualquier momento.
Una persona en un ala delta asciende en espiral como resultado del aire que sube rápidamente, siguiendo una trayectoria con el vector de posición $\mathbf{r}(t) = (3\cos t)\mathbf{i} + (3\sin t)\mathbf{j} + t^2\mathbf{k}$. La trayectoria es similar a la de una hélice, aunque no es una hélice. La gráfica se muestra aquí:
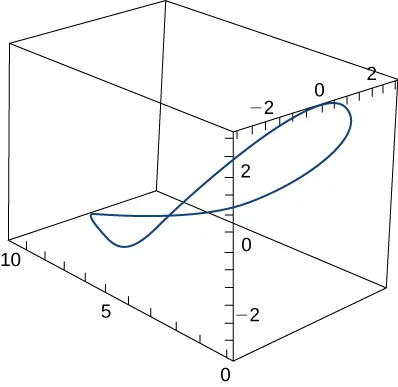
Encuentre las siguientes cantidades:
166. Los vectores de velocidad y aceleración
167. La rapidez del ala delta en cualquier momento
168. Los tiempos, si los hay, en los que la aceleración del ala delta es ortogonal a su velocidad
Dado que $\mathbf{r}(t) = \langle e^{-5t}\sin t, e^{-5t}\cos t, 4e^{-5t} \rangle$ es el vector de posición de una partícula en movimiento, encuentre las siguientes cantidades:
- La velocidad de la partícula.
- La rapidez de la partícula.
- La aceleración de la partícula.
172. Encuentre la rapidez máxima de un punto en la circunferencia de un neumático de automóvil de radio 1 pie cuando el automóvil viaja a 55 mph.
Un proyectil se dispara al aire desde el nivel del suelo con una velocidad inicial de 500 m/seg a un ángulo de 60° con la horizontal. La gráfica se muestra aquí:
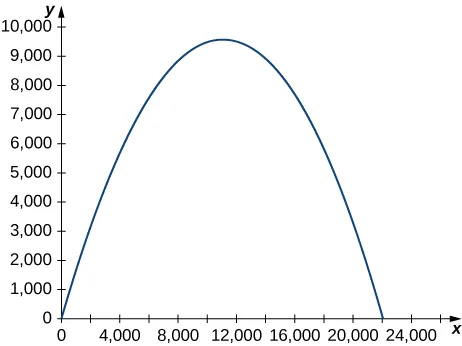
- ¿En qué momento alcanza el proyectil su altura máxima?
- ¿Cuál es la altura máxima aproximada del proyectil?
- ¿En qué momento se alcanza el alcance máximo del proyectil?
- ¿Cuál es el alcance máximo?
- ¿Cuál es el tiempo total de vuelo del proyectil?
Un proyectil se dispara a una altura de 1.5 m sobre el suelo con una velocidad inicial de 100 m/seg y a un ángulo de 30° sobre la horizontal. Use esta información para responder las siguientes preguntas:
- Determine la altura máxima del proyectil.
- Determine el alcance del proyectil.
180. Una pelota de golf es golpeada en dirección horizontal desde el borde superior de un edificio de 100 pies de altura. ¿A qué velocidad debe lanzarse la pelota para aterrizar a 450 pies de distancia?
181. Un proyectil se dispara desde el nivel del suelo a un ángulo de 8° con la horizontal. El proyectil debe tener un alcance de 50 m. Encuentre la velocidad mínima necesaria para lograr este alcance.
182. Demuestre que un objeto que se mueve en línea recta a una rapidez constante tiene una aceleración de cero.
183. La aceleración de un objeto está dada por $\mathbf{a}(t) = t\mathbf{j} + t\mathbf{k}$. La velocidad en $t = 1$ seg es $\mathbf{v}(1) = 5\mathbf{j}$ y la posición del objeto en $t = 1$ seg es $\mathbf{r}(1) = 0\mathbf{i} + 0\mathbf{j} + 0\mathbf{k}$. Encuentre la posición del objeto en cualquier momento.
184. Encuentre $\mathbf{r}(t)$ dado que $\mathbf{a}(t) = -32\mathbf{j}$, $\mathbf{v}(0) = 600\sqrt{3}\mathbf{i} + 600\mathbf{j}$, y $\mathbf{r}(0) = \mathbf{0}$.
185. Encuentre las componentes tangencial y normal de la aceleración para $\mathbf{r}(t) = a\cos(\omega t)\mathbf{i} + a\sin(\omega t)\mathbf{j}$ en $t = 0$.
186. Dado $\mathbf{r}(t) = t^2\mathbf{i} + 2t\mathbf{j}$ y $t = 1$, encuentre las componentes tangencial y normal de la aceleración.
Para cada uno de los siguientes problemas, encuentre las componentes tangencial y normal de la aceleración.
187. $\mathbf{r}(t) = \langle e^t\cos t, e^t\sin t, e^t \rangle$. La gráfica se muestra aquí:
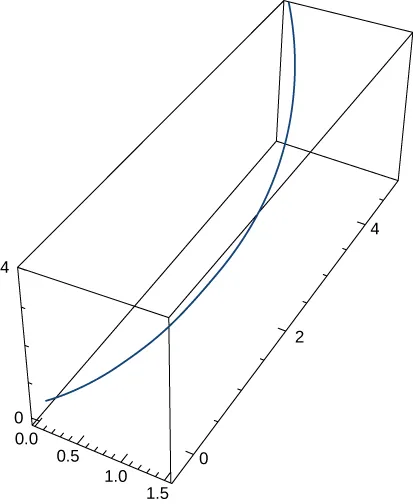
Para cada uno de los siguientes problemas, encuentre las componentes tangencial y normal de la aceleración.
- $\mathbf{r}(t) = \langle \cos(2t), \sin(2t), 1 \rangle$
- $\mathbf{r}(t) = \langle 2t, t^2, \frac{t^3}{3} \rangle$
- $\mathbf{r}(t) = \langle \frac{2}{3}(1+t)^{3/2}, \frac{2}{3}(1-t)^{3/2}, \sqrt{2}t \rangle$
- $\mathbf{r}(t) = \langle 6t, 3t^2, 2t^3 \rangle$
- $\mathbf{r}(t) = t^2\mathbf{i} + t^2\mathbf{j} + t^3\mathbf{k}$
- $\mathbf{r}(t) = 3\cos(2\pi t)\mathbf{i} + 3\sin(2\pi t)\mathbf{j}$
- Encuentre la función vectorial de posición $\mathbf{r}(t)$, dado que $\mathbf{a}(t) = \mathbf{i} + e^t\mathbf{j}$, $\mathbf{v}(0) = 2\mathbf{j}$ y $\mathbf{r}(0) = 2\mathbf{i}$.
- La fuerza sobre una partícula está dada por $\mathbf{f}(t) = (\cos t)\mathbf{i} + (\sin t)\mathbf{j}$. La partícula se encuentra en el punto $(c, 0)$ en $t = 0$. La velocidad inicial de la partícula está dada por $\mathbf{v}(0) = v_0\mathbf{j}$. Encuentre la trayectoria de la partícula de masa $m$. (Recuerde que $\mathbf{F} = m \cdot \mathbf{a}$).
- Un automóvil que pesa 2700 lb toma una curva en una carretera plana mientras viaja a 56 pies/seg. Si el radio de la curva es de 70 pies, ¿cuál es la fuerza de fricción requerida para evitar que el automóvil derrape?
- Utilizando las leyes de Kepler, se puede demostrar que $v_0 = \sqrt{\frac{2GM}{r_0}}$ es la velocidad mínima necesaria cuando $\theta = 0$ para que un objeto escape de la atracción de una fuerza central resultante de una masa $M$. Use este resultado para encontrar la velocidad mínima necesaria cuando $\theta = 0$ para que una cápsula espacial escape de la atracción gravitatoria de la Tierra si la sonda se encuentra a una altitud de 300 km sobre la superficie terrestre.
- Encuentre el tiempo en años que le toma al planeta enano Plutón realizar una órbita alrededor del Sol, dado que $a = 39.5$ U.A.
Resuelva los siguientes problemas relacionados con el movimiento orbital y cinemática avanzada:
- Encuentre la función vectorial de posición $\mathbf{r}(t)$, dado que $\mathbf{a}(t) = \mathbf{i} + e^t\mathbf{j}$, $\mathbf{v}(0) = 2\mathbf{j}$ y $\mathbf{r}(0) = 2\mathbf{i}$.
- La fuerza sobre una partícula está dada por $\mathbf{f}(t) = (\cos t)\mathbf{i} + (\sin t)\mathbf{j}$. La partícula se encuentra en el punto $(c, 0)$ en $t = 0$. La velocidad inicial de la partícula está dada por $\mathbf{v}(0) = v_0\mathbf{j}$. Encuentre la trayectoria de la partícula de masa $m$. (Recuerde que $\mathbf{F} = m \mathbf{a}$).
- Un automóvil que pesa 2700 lb toma una curva en una carretera plana mientras viaja a 56 pies/seg. Si el radio de la curva es de 70 pies, ¿cuál es la fuerza de fricción requerida para evitar que el automóvil derrape?
- Utilizando las leyes de Kepler, se puede demostrar que $v_0 = \sqrt{\frac{2GM}{r_0}}$ es la velocidad mínima necesaria cuando $\theta = 0$ para que un objeto escape de la atracción de una fuerza central resultante de una masa $M$. Use este resultado para encontrar la velocidad mínima necesaria cuando $\theta = 0$ para que una cápsula espacial escape de la atracción gravitatoria de la Tierra si la sonda se encuentra a una altitud de 300 km sobre la superficie terrestre.
- Encuentre el tiempo en años que le toma al planeta enano Plutón realizar una órbita alrededor del Sol, dado que el semieje mayor es $a = 39.5$ U.A.
Suponga que la función de posición de un objeto en tres dimensiones está dada por la ecuación $\mathbf{r}(t) = t\cos(t)\mathbf{i} + t\sin(t)\mathbf{j} + 3t\mathbf{k}$.
- Demuestre que la partícula se mueve sobre un cono circular.
- Encuentre el ángulo entre los vectores de velocidad y aceleración cuando $t = 1.5$.
- Encuentre las componentes tangencial y normal de la aceleración cuando $t = 1.5$.

Muchas gracias por la información. Gran aporte de esta web. Reciba un cordial saludo!
Gracias, bienvenida! 😺
¡Es como si leyeras mi mente, es exactamente como deseaba que me explicaran el tema ! Parece que sabes mucho sobre esto, como si hubieras escrito el libro o algo así. Este es un gran sitio web. Un gran aporte. Definitivamente regresaré.