| 4.3 Máximos y mínimos |

Ejercicios propuestos para el Capítulo 4.3

90. En precálculo, aprendiste una fórmula para la posición del máximo o mínimo de una ecuación cuadrática \(y = ax^2 + bx + c\), que era \(h = -\frac{b}{2a}\). Demuestra esta fórmula usando cálculo.

91. Si estás buscando un mínimo absoluto sobre un intervalo \([a, b]\), ¿por qué necesitas revisar los puntos extremos? Dibuja una gráfica que apoye tu hipótesis.

92. Si estás examinando una función sobre un intervalo \((a, b)\), para \(a\) y \(b\) finitos, ¿es posible no tener un máximo absoluto o un mínimo absoluto?

93. Cuando estás buscando puntos críticos, explica por qué también necesitas determinar los puntos donde \(f'(x)\) no está definida. Dibuja una gráfica para apoyar tu explicación.

94. ¿Puedes tener un máximo absoluto finito para \(y = ax^2 + bx + c\) sobre \((-\infty, \infty)\)? Explica por qué sí o por qué no usando argumentos gráficos.

95. ¿Puedes tener un máximo absoluto finito para \(y = ax^3 + bx^2 + cx + d\) sobre \((-\infty, \infty)\) asumiendo que \(a\) es distinto de cero? Explica por qué sí o por qué no usando argumentos gráficos.

96. Sea \(m\) el número de mínimos locales y \(M\) el número de máximos locales. ¿Puedes crear una función donde \(M > m + 2\)? Dibuja una gráfica para apoyar tu explicación.

97. ¿Es posible tener más de un máximo absoluto? Usa un argumento gráfico para probar tu hipótesis.

98. ¿Es posible no tener ningún mínimo o máximo absoluto para una función? Si es así, construye una función de este tipo. Si no, explica por qué esto no es posible.

99. [T] Grafica la función \(y = e^{ax}\). ¿Para qué valores de \(a\), en cualquier dominio infinito, tendrás un mínimo absoluto y un máximo absoluto?

      Para los siguientes ejercicios, determine dónde ocurren los máximos y mínimos locales y absolutos en la gráfica dada. Asuma que la gráfica representa la totalidad de cada función. Para cualquier extremo ubicado en un punto final, aproxime el valor de x:

100.

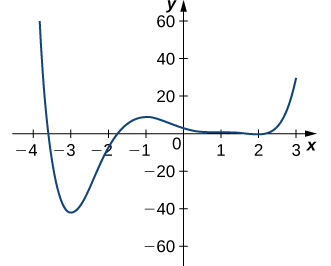
101.

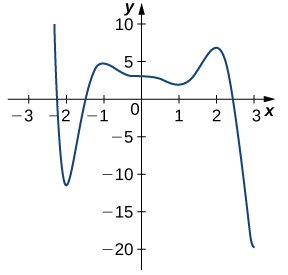
102.

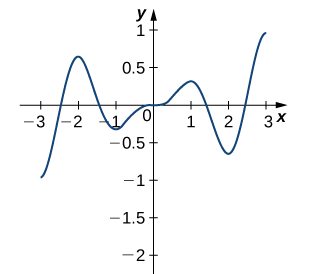
103.

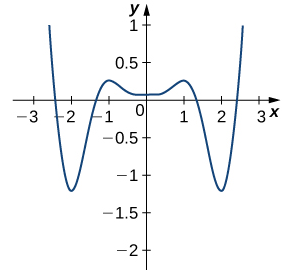
Para los siguientes problemas, dibuja gráficas de \(f(x)\), que es continua, sobre el intervalo \([-4, 4]\) con las siguientes propiedades:

104. Máximo absoluto en \(x = 2\) y mínimos absolutos en \(x = \pm 3\)

105. Mínimo absoluto en \(x = 1\) y máximo absoluto en \(x = 2\)

106. Máximo absoluto en \(x = 4\), mínimo absoluto en \(x = -1\), máximo local en \(x = -2\) y un punto crítico que no es un máximo ni un mínimo en \(x = 2\)

107. Máximos absolutos en \(x = 2\) y \(x = -3\), mínimo local en \(x = 1\) y mínimo absoluto en \(x = 4\)

Para los siguientes ejercicios, encuentra los puntos críticos en los dominios de las siguientes funciones:

108. \(y = 4x^3 – 3x\)

109. \(y = 4\sqrt{x} – x^2\)

110. \(y = \frac{1}{x – 1}\)

111. \(y = \ln(x – 2)\)

112. \(y = \tan(x)\)

113. \(y = \sqrt{4 – x^2}\)

114. \(y = x^{3/2} – 3x^{5/2}\)

115. \(y = \frac{x^2 – 1}{x^2 + 2x – 3}\)

116. \(y = \sin^2(x)\)

117. \(y = x + \frac{1}{x}\)

Para los siguientes ejercicios, encuentra los extremos locales y/o absolutos para las funciones sobre el dominio especificado.

118. \(f(x) = x^2 + 3\) sobre \([-1, 4]\)

119. \(y = x^2 + \frac{2}{x}\) sobre \([1, 4]\)

120. \(y = (x – x^2)^2\) sobre \([-1, 1]\)

121. \(y = \frac{1}{(x – x^2)}\) sobre \((0, 1)\)

122. \(y = \sqrt{9 – x}\) sobre \([1, 9]\)

123. \(y = x + \sin(x)\) sobre \([0, 2\pi]\)

124. \(y = \frac{x}{1 + x}\) sobre \([0, 100]\)

125. \(y = |x + 1| + |x – 1|\) sobre \([-3, 2]\)

126. \(y = \sqrt{x} – \sqrt{x^3}\) sobre \([0, 4]\)

127. \(y = \sin x + \cos x\) sobre \([0, 2\pi]\)

128. \(y = 4\sin \theta – 3\cos \theta\) sobre \([0, 2\pi]\)

Para los siguientes ejercicios, encuentra los mínimos y máximos locales y absolutos para las funciones sobre \((-\infty,\infty)\).

129. \(y=x^{2}+4x+5\)

130. \(y=x^{3}-12x\)

131. \(y=3x^{4}+8x^{3}-18x^{2}\)

132. \(y=x^{3}(1-x)^{6}\)

133. \(y=\frac{x^{2}+x+6}{x-1}\)

134. \(y=\frac{x^{2}-1}{x-1}\)

Para las siguientes funciones, usa una calculadora para graficar la función y estimar los máximos y mínimos absolutos y locales. Luego, resuélvelos explícitamente.

135. [T] \(y = 3x\sqrt{1 – x^2}\)

136. [T] \(y = x + \sin(x)\)

137. [T] \(y = 12x^5 + 45x^4 + 20x^3 – 90x^2 – 120x + 3\)

138. [T] \(y = \frac{x^3 + 6x^2 – x – 30}{x – 2}\)

139. [T] \(y = \frac{\sqrt{4 – x^2}}{\sqrt{4 + x^2}}\)

140. Una compañía que produce teléfonos celulares tiene una función de costo de \(C = x^2 – 1200x + 36400\), donde \(C\) es el costo en dólares y \(x\) es el número de teléfonos celulares producidos (en miles). ¿Cuántas unidades de teléfonos celulares (en miles) minimizan esta función de costo?

141. Una pelota es lanzada al aire y su posición está dada por \(h(t) = -4.9t^2 + 60t + 5\) m. Encuentra la altura a la que la pelota deja de ascender. ¿Cuánto tiempo después de ser lanzada ocurre esto?

Para los siguientes ejercicios, considere la producción de oro durante la fiebre del oro de California (1848-1888). La producción de oro puede ser modelada por

\[G(t)=\frac{(25t)}{(t^{2}+16)}\]

donde \(t\) es el número de años desde que comenzó la fiebre \((0\le t\le40)\) y \(G\) es onzas de oro producidas (en millones). Un resumen de los datos se muestra en la siguiente figura.

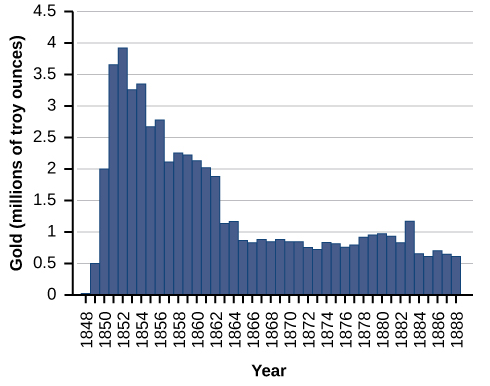
142. Encuentra cuándo ocurrió la máxima producción de oro (local y absoluta), y la cantidad de oro producida durante ese máximo.

143. Encuentra cuándo ocurrió la mínima producción de oro (local y absoluta). ¿Cuál fue la cantidad de oro producida durante este mínimo?

      Encuentra los puntos críticos, máximos y mínimos para las siguientes funciones definidas por partes:

144. \(y = \begin{cases} x^2 – 4x & 0 \le x \le 1 \\ x^2 – 4 & 1 < x \le 2 \end{cases}\)

145. \(y = \begin{cases} x^2 + 1 & x \le 1 \\ x^2 – 4x + 5 & x > 1 \end{cases}\)

Para los siguientes ejercicios, encuentra los puntos críticos de las siguientes funciones genéricas. ¿Son máximos, mínimos o ninguno? Indica las condiciones necesarias:

146. \(y = ax^2 + bx + c\), dado que \(a > 0\)

147. \(y = (x – 1)^a\); dado que \(a > 1\) y a es un entero.