| 5.2 La integral definida |

Ejercicios propuestos para el Capítulo 5.2

      En los siguientes ejercicios, exprese los límites como integrales:

60. \[ \lim_{n \to \infty} \sum_{i=1}^n (x_i^*) \, \Delta x \quad \text{ sobre } [1, 3] \]
61. \[ \lim_{n \to \infty} \sum_{i=1}^n (5(x_i^*)^2 – 3(x_i^*)^3) \, \Delta x \quad \text{ sobre } [0, 2] \]
62. \[ \lim_{n \to \infty} \sum_{i=1}^n \sin^2 (2 \pi x_i^*) \, \Delta x \quad \text{ sobre } [0, 1] \]
63. \[ \lim_{n \to \infty} \sum_{i=1}^n \cos^2 (2 \pi x_i^*) \, \Delta x \quad \text{ sobre } [0, 1] \]

      En los siguientes ejercicios, dadas L_n o R_n como se indica, exprese sus límites cuando n →∞ como integrales definidas, identificando los intervalos correctos:

64. \( L_n = \frac{1}{n} \sum_{i=1}^n \frac{i-1}{n} \)
65. \( R_n = \frac{1}{n} \sum_{i=1}^n \frac{i}{n} \)
66. \( L_n = \frac{2}{n} \sum_{i=1}^n \left( 1 + 2 \frac{i-1}{n} \right) \)
67. \( R_n = \frac{3}{n} \sum_{i=1}^n \left( 3 + 3\frac{i}{n} \right) \)
68. \( L_n = \frac{2\pi}{n} \sum_{i=1}^n 2\pi \frac{i-1}{n} \cos\left( 2\pi \frac{i-1}{n} \right) \)
69. \( R_n = \frac{1}{n} \sum_{i=1}^n \left( 1 + \frac{i}{n} \right) \log\left( \left(1 + \frac{i}{n}\right)^2 \right) \)

      En los siguientes ejercicios, evalúe las integrales de las funciones graficadas utilizando las fórmulas para las áreas de triángulos y círculos, y restando las áreas debajo del eje x:

70.

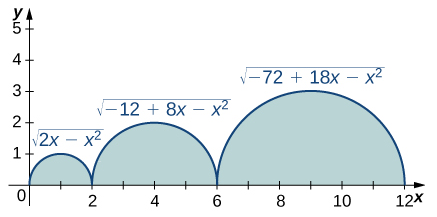
71.

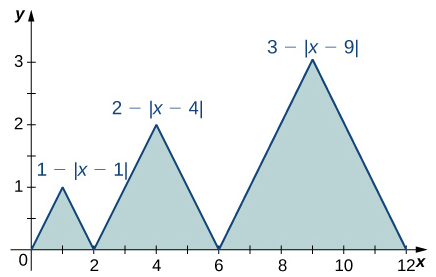
7.2

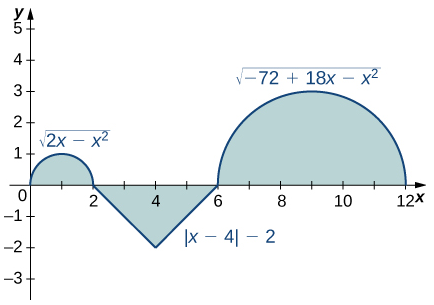
73.

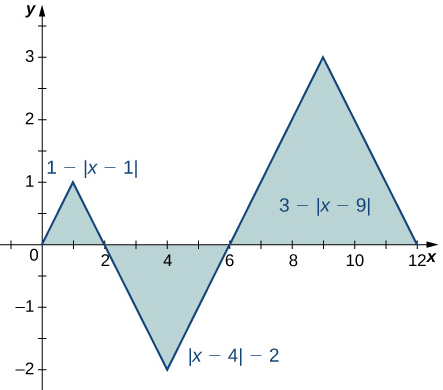
74.

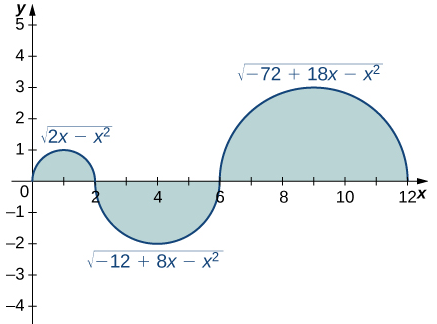
75.

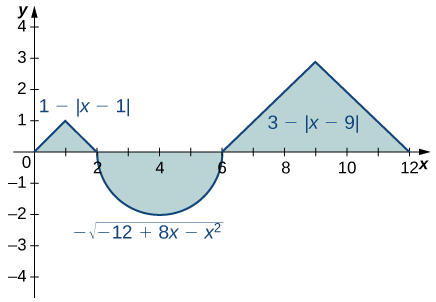
        En los siguientes ejercicios, evalúe la integral usando fórmulas de área:

76. \[ \int_0^3 (3-x) \, dx \]
77. \[ \int_2^3 (3-x) \, dx \]
78. \[ \int_{-3}^3 (3 – |x|) \, dx \]
79. \[ \int_0^6 (3 – |x – 3|) \, dx \]
80. \[ \int_{-2}^2 \sqrt{4 – x^2} \, dx \]
81. \[ \int_1^5 \sqrt{4 – (x-3)^2} \, dx \]
82. \[ \int_0^{12} \sqrt{36 – (x-6)^2} \, dx \]
83. \[ \int_{-2}^3 (3 – |x|) \, dx \]

        En los siguientes ejercicios, use los promedios de los valores en los puntos finales izquierdo (L) y derecho (R) para calcular las integrales de las funciones lineales a trozos con gráficas que pasan por la lista de puntos dada sobre los intervalos indicados:

84. { (0, 0), (2, 1), (4, 3), (5, 0), (6, 0), (8, 3) } sobre \( [0, 8] \)
85. { (0, 2), (1, 0), (3, 5), (5, 5), (6, 2), (8, 0) } sobre \( [0, 8] \)
86. { (-4, -4), (-2, 0), (0, -2), (3, 3), (4, 3) } sobre \( [-4, 4] \)
87. { (-4, 0), (-2, 2), (0, 0), (1, 2), (3, 2), (4, 0) } sobre \( [-4, 4] \)

Suponga que \( \int_0^4 f(x) \, dx = 5 \) y \( \int_0^2 f(x) \, dx = -3 \), y \( \int_0^4 g(x) \, dx = -1 \) y \( \int_0^2 g(x) \, dx = 2 \). En los siguientes ejercicios, calcule las integrales:

88. \[ \int_0^4 (f(x) + g(x)) \, dx \]
89. \[ \int_2^4 (f(x) + g(x)) \, dx \]
90. \[ \int_0^2 (f(x) – g(x)) \, dx \]
91. \[ \int_2^4 (f(x) – g(x)) \, dx \]
92. \[ \int_0^2 (3f(x) – 4g(x)) \, dx \]
93. \[ \int_2^4 (4f(x) – 3g(x)) \, dx \]

En los siguientes ejercicios, use la identidad \[ \int_{-A}^A f(x) \, dx = \int_{-A}^0 f(x) \, dx + \int_0^A f(x) \, dx \] para calcular las integrales:

94. \[ \int_{-\pi}^{\pi} \frac{\sin t}{1 + t^2} \, dt \quad \text{(Pista: } \sin (-t) = -\sin(t)) \]
95. \[ \int_{-\sqrt{\pi}}^{\sqrt{\pi}} \frac{t}{1 + \cos t} \, dt \]

En los siguientes ejercicios, encuentre el área neta con signo entre \( f(x) \) y el eje x:

96. \[ \int_1^3 (2 – x) \, dx \quad \text{(Pista: Mire la gráfica de } f.) \]
97. \[ \int_2^4 (x – 3)^3 \, dx \quad \text{(Pista: Mire la gráfica de } f.) \]

En los siguientes ejercicios, dado que \( \int_0^1 x \, dx = \frac{1}{2} \), \( \int_0^1 x^2 \, dx = \frac{1}{3} \) y \( \int_0^1 x^3 \, dx = \frac{1}{4} \), calcule las integrales:

98. \[ \int_0^1 (1 + x + x^2 + x^3) \, dx \]
99. \[ \int_0^1 (1 – x + x^2 – x^3) \, dx \]
100. \[ \int_0^1 (1 – x)^2 \, dx \]
101. \[ \int_0^1 (1 – 2x)^3 \, dx \]
102. \[ \int_0^1 \left(6x – \frac{4}{3}x^2\right) \, dx \]
103. \[ \int_0^1 (7 – 5x^3) \, dx \]

En los siguientes ejercicios, use el teorema de comparación:

104. \[ \int_0^3 (x^2 – 6x + 9) \, dx \geq 0. \]
105. \[ \int_{-2}^3 (x – 3)(x + 2) \, dx \leq 0. \]
106. \[ \int_0^1 \sqrt{1 + x^3} \, dx \leq \int_0^1 \sqrt{1 + x^2} \, dx. \]
107. \[ \int_1^2 \sqrt{1 + x} \, dx \leq \int_1^2 \sqrt{1 + x^2} \, dx. \]
108. \[ \int_0^{\pi/2} \sin t \, dt \geq \frac{\pi}{4}. \quad (\text{Pista: } \sin t \geq \frac{2t}{\pi} \text{ sobre } \left[0, \frac{\pi}{2}\right]) \]
109. \[ \int_{-\pi/4}^{\pi/4} \cos t \, dt \geq \frac{\pi \sqrt{2}}{4}. \]

En los siguientes ejercicios, encuentre el valor promedio \( f_{\text{ave}} \) de \( f \) entre \( a \) y \( b \), y encuentre un punto \( c \) donde \( f(c) = f_{\text{ave}} \).:

110. \( f(x) = x^2, \quad a = -1, b = 1 \)
111. \( f(x) = x^5, \quad a = -1, b = 1 \)
112. \( f(x) = \sqrt{4 – x^2}, \quad a = 0, b = 2 \)
113. \( f(x) = (3 – |x|), \quad a = -3, b = 3 \)
114. \( f(x) = \sin x, \quad a = 0, b = 2\pi \)
115. \( f(x) = \cos x, \quad a = 0, b = 2\pi \)

En los siguientes ejercicios, aproxime el valor promedio usando sumas de Riemann \( L_{100} \) y \( R_{100} \). ¿Cómo se compara su respuesta con la respuesta exacta dada?:

116. [T] \( y = \ln(x) \) sobre el intervalo \( [1, 4] \); la solución exacta es \( \frac{\ln(256)}{3} – 1 \).
117. [T] \( y = e^{x/2} \) sobre el intervalo \( [0, 1] \); la solución exacta es \( 2(\sqrt{e} – 1) \).
118. [T] \( y = \tan x \) sobre el intervalo \( \left[0, \frac{\pi}{4}\right] \); la solución exacta es \( \frac{2 \ln(2)}{\pi} \).
119. [T] \( y = \frac{x+1}{\sqrt{4-x^2}} \) sobre el intervalo \( [-1, 1] \); la solución exacta es \( \frac{\pi}{6} \).

En los siguientes ejercicios, calcule el valor promedio usando las sumas de Riemann izquierdas \( L_N \) para \( N = 1, 10, 100 \). ¿Cómo se compara la precisión con el valor exacto dado?:

120. [T] \( y = x^2 – 4 \) sobre el intervalo \( [0, 2] \); la solución exacta es \( -\frac{8}{3} \).
121. [T] \( y = xe^{x^2} \) sobre el intervalo \( [0, 2] \); la solución exacta es \( \frac{1}{4} (e^4 – 1) \).
122. [T] \( y = \left(\frac{1}{2}\right)^x \) sobre el intervalo \( [0, 4] \); la solución exacta es \( \frac{15}{64 \ln(2)} \).
123. [T] \( y = x \sin(x^2) \) sobre el intervalo \( [-\pi, 0] \); la solución exacta es \( \frac{\cos(\pi^2) – 1}{2\pi} \).

124. Suponga que \( A = \int_0^{2\pi} \sin^2 t \, dt \) y \( B = \int_0^{2\pi} \cos^2 t \, dt \). Muestre que \( A + B = 2\pi \) y \( A = B \).
125. Suponga que \( A = \int_{-\pi/4}^{\pi/4} \sec^2 t \, dt \) y \( B = \int_{-\pi/4}^{\pi/4} \tan^2 t \, dt \). Muestre que \( A – B = \frac{\pi}{2} \).
126. Muestre que el valor promedio de \( \sin^2 t \) sobre \( [0, 2\pi] \) es igual a 1/2. Sin más cálculos, determine si el valor promedio de \( \sin^2 t \) sobre \( [0, \pi] \) también es igual a 1/2.
127. Muestre que el valor promedio de \( \cos^2 t \) sobre \( [0, 2\pi] \) es igual a 1/2. Sin más cálculos, determine si el valor promedio de \( \cos^2 (t) \) sobre \( [0, \pi] \) también es igual a 1/2.
128. Explique por qué las gráficas de una función cuadrática (parábola) \( p(x) \) y una función lineal \( \ell(x) \) pueden intersecarse en, como máximo, dos puntos. Suponga que \( p(a) = \ell(a) \) y \( p(b) = \ell(b) \), y que \[ \int_a^b p(t) \, dt > \int_a^b \ell(t) \, dt. \] Explique por qué \( \int_c^d p(t) \, dt > \int_c^d \ell(t) \, dt \) siempre que \( a \leq c < d \leq b \).
129. Suponga que la parábola \( p(x) = ax^2 + bx + c \) se abre hacia abajo \( (a < 0) \) y tiene un vértice de \( y = -\frac{b}{2a} > 0 \). ¿Para qué intervalo \( [A, B] \) es \( \int_A^B (ax^2 + bx + c) \, dx \) tan grande como sea posible?

130. Suponga que \( [a, b] \) se puede subdividir en subintervalos \( a = a_0 < a_1 < a_2 < \cdots < a_N = b \) tal que ya sea \( f \geq 0 \) sobre \( [a_{i-1}, a_i] \) o \( f \leq 0 \) sobre \( [a_{i-1}, a_i] \). Establezca \( A_i = \int_{a_{i-1}}^{a_i} f(t) \, dt \).

a. Explique por qué

\[ \int_a^b f(t) \, dt = A_1 + A_2 + \cdots + A_N. \]

b. Luego, explique por qué

\[ \left| \int_a^b f(t) \, dt \right| \leq \int_a^b |f(t)| \, dt. \]

131. Suponga que \( f \) y \( g \) son funciones continuas tales que \[ \int_c^d f(t) \, dt \leq \int_c^d g(t) \, dt \] para cada subintervalo \( [c, d] \) de \( [a, b] \). Explique por qué \( f(x) \leq g(x) \) para todos los valores de \( x \).
132. Suponga que el valor promedio de \( f \) sobre \( [a, b] \) es 1 y el valor promedio de \( f \) sobre \( [b, c] \) es 1 donde \( a < c < b \). Muestre que el valor promedio de \( f \) sobre \( [a, c] \) también es 1.
133. Suponga que \( [a, b] \) se puede dividir. Tomando \( a = a_0 < a_1 < \cdots < a_N = b \) tal que el valor promedio de \( f \) sobre cada subintervalo \( [a_{i-1}, a_i] \) = 1 es igual a 1 para cada \( i = 1, \dots, N \). Explique por qué el valor promedio de \( f \) sobre \( [a, b] \) también es igual a 1.
134. Suponga que para cada \( i \) tal que \( 1 \leq i \leq N \) uno tiene \[ \int_{i-1}^i f(t) \, dt = i. \] Muestre que \[ \int_0^N f(t) \, dt = \frac{N(N+1)}{2}. \]
135. Suponga que para cada \( i \) tal que \( 1 \leq i \leq N \) uno tiene \[ \int_{i-1}^i f(t) \, dt = i^2. \] Muestre que \[ \int_0^N f(t) \, dt = \frac{N(N+1)(2N+1)}{6}. \]

136. [T] Calcule las sumas de Riemann izquierda y derecha \( L_{10} \) y \( R_{10} \) y su promedio \( \frac{L_{10} + R_{10}}{2} \) para \( f(t) = t^2 \) sobre el intervalo \( [0, 1] \). Dado que \( \int_0^1 t^2 \, dt = 0.\overline{33} \), ¿a cuántos decimales es preciso \( \frac{L_{10} + R_{10}}{2} \)?
137. [T] Calcule las sumas de Riemann izquierda y derecha \( L_{10} \) y \( R_{10} \) y su promedio \( \frac{L_{10} + R_{10}}{2} \) para \( f(t) = (4 – t^2) \) sobre el intervalo \( [1, 2] \). Dado que \( \int_1^2 (4 – t^2) \, dt = 1.\overline{66} \), ¿a cuántos decimales es preciso \( \frac{L_{10} + R_{10}}{2} \)?
138. Si \( \int_1^5 \sqrt{1 + t^4} \, dt = 41.7133… \), ¿cuánto es \( \int_1^5 \sqrt{1 + u^4} \, du \)?
139. Estime \( \int_0^1 t \, dt \) usando las sumas de puntos finales izquierdos y derechos, cada una con un solo rectángulo. ¿Cómo se compara el promedio de estas sumas de puntos finales izquierdos y derechos con el valor real de \( \int_0^1 t \, dt \)?
140. Estime \( \int_0^1 t \, dt \) por comparación con el área de un solo rectángulo con altura igual al valor de \( t \) en el punto medio \( t = \frac{1}{2} \). ¿Cómo se compara esta estimación de punto medio con el valor real de \( \int_0^1 t \, dt \)?
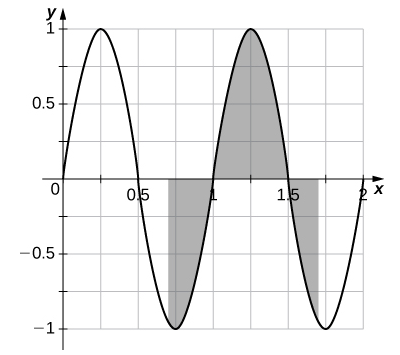
141. A partir de la gráfica de \( \sin(2 \pi x) \) mostrada:

     a. Explique por qué \[ \int_0^1 \sin(2\pi t) \, dt = 0. \]

     b. Explique por qué, en general, \[ \int_a^{a+1} \sin(2\pi t) \, dt = 0 \] para cualquier valor de \( a \).

142. Si \( f \) es 1-periódica \( (f(t+1) = f(t)) \), impar e integrable sobre \( [0, 1] \), ¿es siempre cierto que \[ \int_0^1 f(t) \, dt = 0? \]
143. Si \( f \) es 1-periódica y \[ \int_0^1 f(t) \, dt = A \], ¿es necesariamente cierto que \[ \int_a^{1+a} f(t) \, dt = A \] para toda \( a \)?