| 3. La derivada | Ejercicios propuestos del Capítulo 3.2 |
3.2 La derivada como función
Objetivos de aprendizaje:
3.2.1. Definir la función derivada de una función.
3.2.2. Graficar una función derivada a partir de la gráfica de una función dada.
3.2.3. Indicar la conexión entre derivadas y continuidad.
3.2.4. Describir tres condiciones para cuando una función no tiene una derivada.
3.2.5. Explicar el significado de una derivada de orden superior.
Como hemos visto, la derivada de una función en un punto dado nos da la tasa de cambio o la pendiente de la recta tangente a la función en ese punto. Si diferenciamos una función de posición en un momento dado, obtenemos la velocidad en ese momento. Parece razonable concluir que conocer la derivada de la función en cada punto produciría información valiosa sobre el comportamiento de la función, razonamiento correcto. Sin embargo, el proceso de encontrar la derivada incluso en un puñado de valores utilizando las técnicas de la sección anterior rápidamente se volvería bastante tedioso. En esta sección definimos la función derivada y aprendemos un proceso para encontrarla.
La derivada de una función
La función derivada proporciona la derivada de una función en cada punto del dominio de la función original para la que se define la derivada. Podemos definir formalmente una función derivada de la siguiente manera.
DEFINICIÓN 3.2_1. La función derivada o la derivada de una función
Sea y = f (x) una función. La función derivada de f, denotada por f ′, es una función en x tal que el siguiente límite existe:
\[f'(x) = \lim_{h \to 0} \frac{f(x + h) – f(x)}{h}.\]♦
Se dice que una función f (x) es diferenciable en a si existe f ′(a). De manera más general, se dice que una función es diferenciable en un conjunto abierto S si es diferenciable en cada punto del conjunto S, y una función diferenciable es aquella en la que f ′(x) existe en su dominio.
En los siguientes ejemplos ilustrativos usamos la ecuación proporcionada en la definición 3.2_1 para encontrar la derivada de una función.
Ejemplo ilustrativo 3.2_1. Encontrar la derivada de una función de raíz cuadrada
Encuentre la derivada de f (x) = √x.
Solución:
Comience directamente con la definición de la función derivada.
Sustituya f (x + h) = √(x + h) y f (x) = √x en f ′ (x) = limh → 0 [f (x + h) – f (x)]/h:
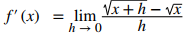
Multiplique el numerador y el denominador por √(x + h) + √x sin distribuir en el denominador:
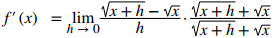
Multiplique los numeradores y simplifique:
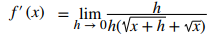
Cancele la h:
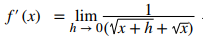
Por último, evalúe el límite:
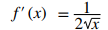
♦
Ejemplo ilustrativo 3.2_2. Encontrar la derivada de una función cuadrática
Encuentre la derivada de la función f (x) = x² − 2x.
Solución:
Siga el mismo procedimiento aquí que en la solución del ejemplo anterior, pero sin tener que multiplicar por el conjugado.
Sustituya f (x + h) = (x + h)² – 2(x + h) y f (x) = x² – 2x en f ′ (x) = limh → 0 [f (x + h) – f (x)]/h:

Expanda (x + h)² – 2(x + h):
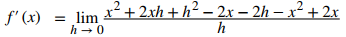
Reduzca términos semejantes:
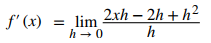
Factorice por h en el numerador:

Cancele el factor común h:

Por último, evalúe el límite:
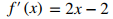
♦
Ejercicio de control 3.2.1
Encuentra la derivada de \(f(x) = x^2\). ♦
Se puede usar una variedad de notaciones diferentes para expresar la derivada de una función. En el ejemplo 3.2_2 mostramos que si f (x) = x² − 2x, entonces f ′(x) = 2x − 2. Si hubiéramos expresado esta función en la forma y = x² − 2x, podríamos haber expresado la derivada como y′ = 2x − 2 o dy/dx = 2x − 2. Podríamos haber transmitido la misma información escribiendo d/dx (x² − 2x) = 2x − 2. Por lo tanto, para la función y = f (x), cada una de las siguientes notaciones representa la derivada de f (x):
\[f'(x), \frac{dy}{dx}, y’, \frac{d}{dx}(f(x)).\]En lugar de f ′(a) también podemos usar
\[\frac{dy}{dx}\Big|_{x=a}\]El uso de la notación dy/dx (llamada notación de Leibniz) es bastante común en ingeniería y física. Para comprender mejor esta notación, recuerde que la derivada de una función en un punto es el límite de las pendientes de las rectas secantes a medida que estas rectas secantes se acercan a la recta tangente. Las pendientes de las rectas secantes a menudo se expresan en la forma Δy/Δx donde Δy es la diferencia en los valores de y correspondientes a la diferencia en los valores de x, que se expresan como Δx (Figura 3.2_1). Así, la derivada, que puede considerarse como la tasa de cambio instantánea de y con respecto a x, se expresa como
\[\frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}.\]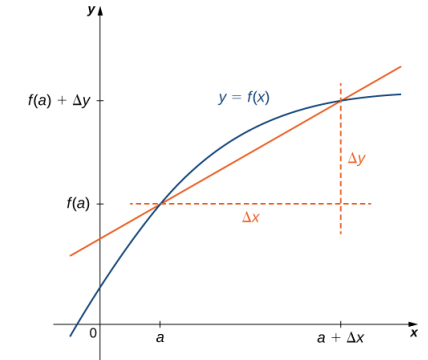
Graficando una derivada
Ya hemos discutido cómo graficar una función, por lo tanto, dada la ecuación de una función o la ecuación de una función derivada, podríamos graficarla. Dado ambos, esperaríamos ver una correspondencia entre las gráficas de estas dos funciones, ya que f ′(x) da la tasa de cambio de una función f (x) (o pendiente de la recta tangente a f (x)).
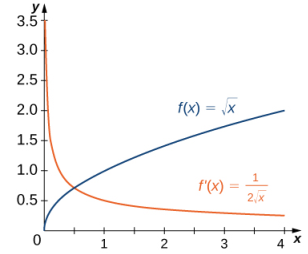
En el ejemplo 3.2_1 encontramos que para f (x) = √x, f ′(x) = 1/√x. Si graficamos estas funciones en los mismos ejes, como en la Figura 3.1_2, podemos usar las gráficas para comprender la relación entre estas dos funciones. Primero, notamos que f (x) está aumentando en todo su dominio, lo que significa que las pendientes de sus rectas tangentes en todos los puntos son positivas. En consecuencia, esperamos f ′(x) > 0 para todos los valores de x en su dominio. Además, a medida que x aumenta, las pendientes de las rectas tangentes a f (x) disminuyen y esperamos ver una disminución correspondiente en f ′(x). También observamos que f (0) no está definida y que el limx→ 0+ f ′(x) = + ∞, correspondiente a una tangente vertical a f (x) en 0.
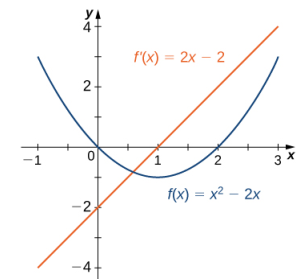
En el ejemplo 3.2_2 encontramos que para f (x) = x² − 2x, f ′(x) = 2x − 2. Las gráficas de estas funciones se muestran en la figura 3.1_3. Observe que f (x) está decreciendo para x < 1. Para estos mismos valores de x, f ′(x) < 0. Para valores de x > 1, f (x) aumenta y f ′ (x) > 0. Además, f (x) tiene una tangente horizontal en x = 1 y f ′(1) = 0.
Ejemplo ilustrativo 3.2_3. Trazar la gráfica de una derivada usando una función
Use la siguiente gráfica de una función f (x) para dibujar la gráfica correspondiente de f ′(x).
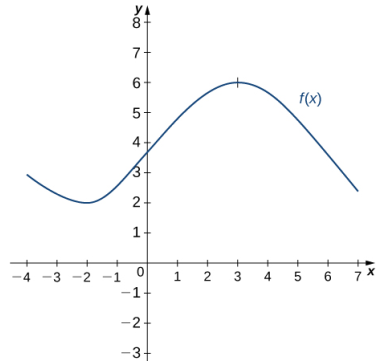
Solución:
La solución se muestra en la siguiente gráfica. Observe que f (x) está creciendo y f ′(x) > 0 en (–2, 3). Además, f (x) está decreciendo y f ′(x) < 0 en (−∞, −2) y en (3, +∞). También tenga en cuenta que f (x) tiene tangentes horizontales en –2 y 3, y f ′(- 2) = 0 y f ′(3) = 0.
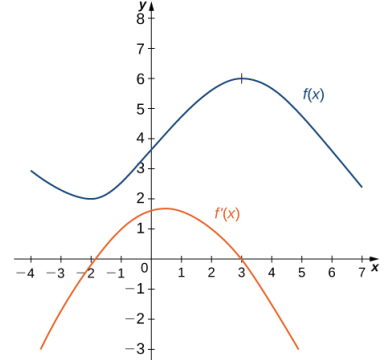
♦
Ejercicio de control 3.2.2
Esboce la gráfica de \(f(x) = x^2 – 4\). ¿En qué intervalo está la gráfica de \(f'(x)\) por encima del eje x? ♦
Derivadas y Continuidad
Ahora que podemos graficar la derivada de una función conociendo la gráfica de la función, examinemos el comportamiento de estas gráficas. Primero, consideramos la relación entre diferenciabilidad y continuidad. Veremos que si una función es diferenciable en un punto, debe ser continua allí; sin embargo, una función que es continua en un punto no necesita ser diferenciable en ese punto. De hecho, una función puede ser continua en un punto y no ser diferenciable en el punto por una de varias razones.
TEOREMA 3.1.1. La diferenciabilidad implica continuidad
Sea f (x) una función y a un número en su dominio. Si f (x) es diferenciable en a, entonces f es continua en a. ♦
Demostración:
Si f (x) es diferenciable en a, entonces f ′(a) existe y
Queremos mostrar que f (x) es continua en a mostrando que limx → a f (x) = f (a). Así,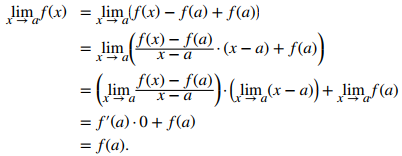 Por lo tanto, dado que f (a) está definido y limx → a f (x) = f (a), concluimos que f es continua en a. ♦
Por lo tanto, dado que f (a) está definido y limx → a f (x) = f (a), concluimos que f es continua en a. ♦
Acabamos de demostrar que la diferenciabilidad implica continuidad, pero ahora consideramos si la continuidad implica diferenciabilidad. Para determinar una respuesta a esta pregunta, examinamos la función valor absoluto f (x) = |x|. Esta función es continua en todas partes; sin embargo, f ‘(0) no está definida. Esta observación nos lleva a creer que la continuidad no implica diferenciabilidad. Exploremos más a fondo. Para f (x) = |x|,
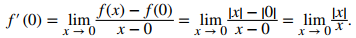
Este límite no existe porque

Vea la Figura 3.2_4:

Consideremos algunas situaciones adicionales en las que una función continua no puede ser diferenciable. Considere la función

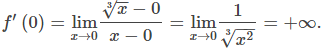
Por lo tanto, f ‘(0) no existe. Un vistazo rápido a la gráfica de f (x) aclara la situación. La función tiene una recta tangente vertical en 0 (Figura 3.2_5).

 tiene una tangente vertical en x = 0. Es continua en 0 pero no es diferenciable en 0.
tiene una tangente vertical en x = 0. Es continua en 0 pero no es diferenciable en 0.La función

también tiene una derivada que exhibe un comportamiento interesante en 0. Vemos que

Este límite no existe, esencialmente porque las pendientes de las rectas secantes cambian continuamente de dirección a medida que se acercan a cero:
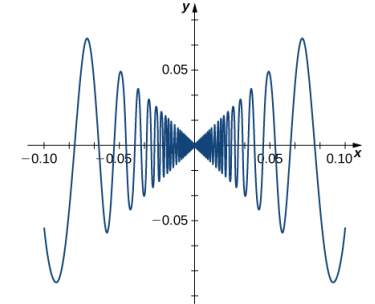
En resumen:
- Observamos que si una función no es continua, no puede ser diferenciable, ya que cada función diferenciable debe ser continua. Sin embargo, si una función es continua, aún puede no ser diferenciable.
- Vimos que f (x) = |x| no se pudo diferenciar en 0 porque el límite de las pendientes de las rectas tangentes a la izquierda y a la derecha no era el mismo. Visualmente, esto resultó en una esquina aguda en el gráfico de la función en 0. De esto concluimos que para ser diferenciable en un punto, una función debe ser “suave” en ese punto.
- Como vimos en el ejemplo de
 una función no puede diferenciarse en un punto donde hay una recta tangente vertical.
una función no puede diferenciarse en un punto donde hay una recta tangente vertical. - Como lo vimos con
 una función puede no ser diferenciable en un punto de formas más complicadas también.
una función puede no ser diferenciable en un punto de formas más complicadas también.
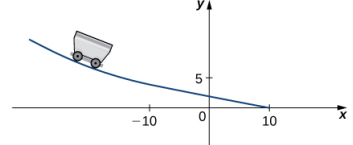
Ejemplo ilustrativo 3.2_4. Una función por partes que es continua y diferenciable
Una empresa de juguetes quiere diseñar una pista para un automóvil de juguete que comience a lo largo de una curva parabólica y luego se convierta en una línea recta (Figura 3.2_7). La función que describe la forma que debe tener la pista es

donde x y f (x) están en pulgadas. Para que el automóvil se mueva suavemente a lo largo de la pista, la función f (x) debe ser continua y diferenciable en −10. Encuentre valores de b y c que hagan que f (x) sea continua y diferenciable.
Solución:
Para que la función sea continua en x = −10, limx → 10− f (x) = f (−10). Por lo tanto, ya que

y f (−10) = 5, debemos tener 10 − 10b + c = 5. De manera equivalente, tenemos que c = 10b − 5.
Para que la función sea diferenciable en −10,
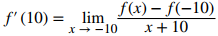
debe existir Dado que f (x) se define usando diferentes reglas a la derecha y a la izquierda, debemos evaluar este límite desde la derecha y la izquierda y luego establecerlos iguales entre sí:

también tenemos que

Esto nos da b − 2 = −1/4. Así b = 7/4 y c = 10 (7/4) −5 = 25/2. ♦
Ejercicio de control 3.2.3
Encuentra los valores de \(a\) y \(b\) que hacen que \(f(x) = \begin{cases} ax + b, & \text{si } x < 3 \\ x^2, & \text{si } x \ge 3 \end{cases}\) sea continua y diferenciable en 3. ♦
Derivadas de orden superior
La derivada de una función es en sí misma una función, por lo que podemos encontrar la derivada de una derivada. Por ejemplo, la derivada de una función de posición es la tasa de cambio de posición o velocidad. La derivada de la velocidad es la tasa de cambio de velocidad, que es la aceleración. La nueva función obtenida al diferenciar la derivada se llama la segunda derivada. Además, podemos continuar tomando derivadas para obtener la tercera derivada, cuarta derivada, etc. Colectivamente, estos se denominan derivadas de orden superior. La notación para las derivadas de orden superior de y = f (x) se puede expresar en cualquiera de las siguientes formas:
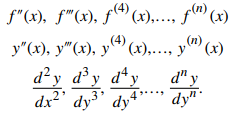
Es interesante notar que la notación para la segunda derivada

puede ser visto como un simbolismo par expresar

de una manera más compacta. Análogamente

Ejemplo ilustrativo 3.2_5. Hallando una segunda derivada
Para f (x) = 2x² − 3x + 1, encuentre f ″(x).
Solución:
Primero encuentra f ′(x):

Luego, encuentre f ″(x) tomando la derivada de f ′(x) = 4x − 3:

♦
Ejercicio de control 3.2.4
Encuentra \(f”(x)\) para \(f(x) = x^2\).
Ejemplo ilustrativo 3.2_65. Encontrar una aceleración
La posición de una partícula a lo largo de un eje de coordenadas en el tiempo t (en segundos) viene dada por s (t)= 3t² − 4t + 1 (en metros). Encuentre la función que describe su aceleración en el tiempo t.
Solución:
Como v(t) = s′(t) y a(t) = v′(t) = s″(t), comenzamos por calcular la derivada de s(t):

Luego, calculamos la segunda derivada de s(t):

De tal manera que, la aceleración de esta partícula es:
a = 6 m/s². ♦
Ejercicio de control 3.2.5
Dada la función \(s(t) = t^3\), encuentra \(a(t)\).

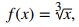 una función no puede diferenciarse en un punto donde hay una recta tangente vertical.
una función no puede diferenciarse en un punto donde hay una recta tangente vertical.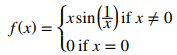 una función puede no ser diferenciable en un punto de formas más complicadas también.
una función puede no ser diferenciable en un punto de formas más complicadas también.