| 9. Ecuaciones diferenciales |
9.1. Introducción a las ecuaciones diferenciales
Objetivos de aprendizaje
En este CAPÍTULO 9.1 Comenzamos nuestro estudio de las ecuaciones diferenciales.
La SECCIÓN 9.1.1 Presenta ejemplos de aplicaciones que conducen a ecuaciones diferenciales.
La SECCIÓN 9.1.2 Introduce conceptos y definiciones básicos sobre ecuaciones diferenciales.
La SECCIÓN 9.1.3 Presenta un método geométrico para tratar ecuaciones diferenciales que se conoce desde hace mucho tiempo, pero que se ha vuelto particularmente útil e importante con la proliferación en la actualidad de software de ecuaciones diferenciales fácilmente disponible.
9.1.1. APLICACIONES QUE LLEVAN A ECUACIONES DIFERENCIALES
Para aplicar métodos matemáticos a un problema físico o de la “vida real”, debemos formular el problema en términos matemáticos; es decir, debemos construir un modelo matemático para el problema. Muchos problemas físicos se refieren a las relaciones entre cantidades cambiantes. Dado que las tasas de cambio están representadas matemáticamente por derivadas, los modelos matemáticos a menudo involucran ecuaciones que relacionan una función desconocida y una o más de sus derivadas. Tales ecuaciones se denominan ecuaciones diferenciales. Son el tema de estudio de estas lecciones.
Gran parte del cálculo se dedica al aprendizaje de técnicas matemáticas que se aplican en cursos posteriores de matemáticas y ciencias; no tendrías tiempo para aprender mucho cálculo si insistieras en ver una aplicación específica de cada tema cubierto en el curso. Del mismo modo, gran parte de las presentes lecciones está dedicado a métodos que pueden aplicarse en cursos posteriores. Solo una parte relativamente pequeña de los capítulos está dedicada a la obtención de ecuaciones diferenciales específicas de modelos matemáticos, o relacionando las ecuaciones diferenciales que estudiamos con aplicaciones específicas. En esta sección mencionamos algunas de estas aplicaciones.
El modelo matemático para un problema aplicado es casi siempre más simple que la situación real que se estudia, ya que generalmente se requieren suposiciones simplificadoras para obtener un problema matemático que se pueda resolver utilizando las técnicas matemáticas disponibles. Por ejemplo, al modelar el movimiento de un objeto que cae, podríamos no tomar en cuenta la resistencia del aire ni la atracción gravitacional de cuerpos celestes, distintos a la Tierra, que ejercen sobre el objeto, o al modelar el crecimiento de una población, podríamos suponer que la población crece continuamente en lugar de en pasos discretos.
Un buen modelo matemático tiene dos propiedades importantes:
• Es lo suficientemente simple como para que se pueda resolver el problema matemático.
• Representa la situación real lo suficientemente bien como para que la solución al problema matemático prediga el resultado del problema real con un grado útil de precisión. Si los resultados pronosticados por el modelo no concuerdan con las observaciones físicas, los supuestos subyacentes del modelo deben revisarse hasta que se obtenga un acuerdo satisfactorio.
Ahora daremos ejemplos de modelos matemáticos que involucran ecuaciones diferenciales. Volveremos a estos problemas en los momentos apropiados, a medida que aprendamos cómo resolver los diversos tipos de ecuaciones diferenciales que ocurren en los modelos.
Todos los ejemplos en esta sección tratan con funciones cuya variable independiente es el tiempo, y que denotamos por t. Si y es una función de t, y′ denota la derivada de y con respecto a t; así
Crecimiento y decrecimiento de una población
Aunque el número de individuos de una población (personas en un país determinado, bacterias en un cultivo de laboratorio, flores silvestres en un bosque, etc.) en un momento dado t es necesariamente un número entero (variable discreta), los modelos que usan ecuaciones diferenciales para describir el crecimiento y el decrecimiento de las poblaciones generalmente se basan en el supuesto simplificador de que el número de miembros de la población puede considerarse como una función diferenciable de variable continua P = P(t). En la mayoría de los modelos de crecimiento y decrecimiento se supone que la ecuación diferencial toma la forma
P′ = a(P)P, (9.1.1_1)
donde a es una función continua de P; P′ representa la tasa de cambio de la población por unidad de tiempo por individuo. En el modelo maltusiano, se supone que a(P) es una constante, por lo que P′ = a(P)P se convierte en
P′ = aP. (9.1.1_2)
Este modelo supone que los números de nacimientos y muertes por unidad de tiempo son ambos proporcionales a la población. Las constantes de proporcionalidad son la tasa de natalidad (nacimientos por unidad de tiempo por individuo) y la tasa de mortalidad (muertes por unidad de tiempo por individuo); a es la tasa de natalidad menos la tasa de mortalidad. Aprendiste en el cálculo que si c es alguna constante, entonces
 (9.1.1_3)
(9.1.1_3)
satisface (9.1.1_2), de tal modo que (9.1.1_2) tiene infinitas soluciones (una para cada valor de c). Para seleccionar la solución del problema específico que estamos considerando, debemos conocer la población P₀ en un momento inicial, digamos t = 0. Establecer t = 0 en (9.1.1_3) produce c = P(0) = P₀, entonces la solución aplicable es

Esto implica que

es decir, la población tiende al infinito si la tasa de natalidad excede la tasa de mortalidad, o tiende a cero si la tasa de mortalidad excede la tasa de natalidad.
Para ver las limitaciones del modelo maltusiano, supongamos que estamos modelando la población de un país, comenzando desde un tiempo t = 0 cuando la tasa de natalidad excede la tasa de mortalidad (a > 0), y los recursos del país en términos de espacio, suministro de alimentos y otras necesidades de la vida pueden apoyar a la población existente. Entonces, la predicción dada por la función 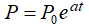 puede ser razonablemente precisa siempre que permanezca dentro de los límites que los recursos del país pueden soportar. Sin embargo, el modelo inevitablemente debe perder validez cuando la predicción excede estos límites. (¡Si nada más, eventualmente no habrá suficiente espacio para la población prevista!)
puede ser razonablemente precisa siempre que permanezca dentro de los límites que los recursos del país pueden soportar. Sin embargo, el modelo inevitablemente debe perder validez cuando la predicción excede estos límites. (¡Si nada más, eventualmente no habrá suficiente espacio para la población prevista!)
Este defecto en el modelo maltusiano sugiere la necesidad de un modelo que tenga en cuenta las limitaciones de espacio y recursos que tienden a oponerse a la tasa de crecimiento de la población a medida que aumenta la población. Quizás el modelo más famoso de este tipo es el modelo Verhulst, donde (9.1.1_2) se reemplaza por
P′ = aP(1 − αP), (9.1.1_4)
donde α es una constante positiva. Mientras P sea pequeño comparado con 1/α, la razón P′/P es aproximadamente igual a a. Por lo tanto, el crecimiento es aproximadamente exponencial; sin embargo, a medida que P aumenta, la relación P′/P disminuye a medida que los factores opuestos se vuelven significativos.
La ecuación (9.1.1_4) es la ecuación logística. Aprenderá cómo resolverla en la Sección 9.2.2 (Consulte el Ejercicio 9.2.2.28.) La solución es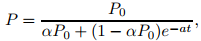 donde P0 = P(0) > 0. Por lo tanto, limt→∞ P(t) = 1/α, independiente de P0.
donde P0 = P(0) > 0. Por lo tanto, limt→∞ P(t) = 1/α, independiente de P0.
La figura 9.1.1_1 muestra gráficos típicos de P versus t para varios valores de P0:

La ley de enfriamiento de Newton
Según la ley de enfriamiento de Newton, la temperatura de un cuerpo cambia a un ritmo proporcional a la diferencia entre la temperatura del cuerpo y la temperatura del medio circundante. Por lo tanto, si Tm es la temperatura del medio y T = T(t) es la temperatura del cuerpo en el tiempo t, entonces donde k es una constante positiva y el signo menos indica que la temperatura del cuerpo aumenta con el tiempo si es menor que la temperatura del medio, o disminuye si es mayor. Más adelante veremos que si Tm es constante, entonces la solución de la ecuación diferencial (9.1.1_5) es (Ver solución dada por ChatGPT)
donde k es una constante positiva y el signo menos indica que la temperatura del cuerpo aumenta con el tiempo si es menor que la temperatura del medio, o disminuye si es mayor. Más adelante veremos que si Tm es constante, entonces la solución de la ecuación diferencial (9.1.1_5) es (Ver solución dada por ChatGPT) donde To es la temperatura del cuerpo cuando t = 0. Por lo tanto, limt→∞ T(t) = Tm, independiente de T₀. (El sentido común sugiere esto. ¿Por qué?)
donde To es la temperatura del cuerpo cuando t = 0. Por lo tanto, limt→∞ T(t) = Tm, independiente de T₀. (El sentido común sugiere esto. ¿Por qué?)
La figura 9.1.1_2 muestra gráficos típicos de T versus t para varios valores de T₀.

Asumir que el medio permanece a temperatura constante parece razonable si estamos considerando enfriar una taza de café en una habitación, pero no si estamos enfriando un enorme caldero de metal fundido en la misma habitación. La diferencia entre las dos situaciones es que no es probable que el calor perdido por el café incremente la temperatura de la habitación de manera apreciable, pero sí el calor perdido por el metal que se está enfriando. En esta segunda situación, debemos usar un modelo que explique el calor intercambiado entre el objeto y el medio.
Sean T = T(t) y Tm = Tm(t) las temperaturas del objeto y el medio respectivamente, y sean T₀ y Tm₀ sus valores iniciales respectivos. Nuevamente, asumimos que T y Tm están relacionados por la ecuación diferencial También suponemos que el cambio en el calor del objeto a medida que su temperatura cambia de T₀ a T es a(T − T₀) y el cambio en el calor del medio a medida que su temperatura cambia de Tm₀ a Tm es am(Tm – Tm₀), donde a y am son constantes positivas dependiendo de las masas y las propiedades térmicas del objeto y el medio, respectivamente. Si además suponemos que el calor total del objeto y el medio permanece constante (es decir, la energía se conserva), entonces
También suponemos que el cambio en el calor del objeto a medida que su temperatura cambia de T₀ a T es a(T − T₀) y el cambio en el calor del medio a medida que su temperatura cambia de Tm₀ a Tm es am(Tm – Tm₀), donde a y am son constantes positivas dependiendo de las masas y las propiedades térmicas del objeto y el medio, respectivamente. Si además suponemos que el calor total del objeto y el medio permanece constante (es decir, la energía se conserva), entonces Resolver esto para Tm y sustituir el resultado en (9.1.1_5) da como resultado la ecuación diferencial
Resolver esto para Tm y sustituir el resultado en (9.1.1_5) da como resultado la ecuación diferencial
para la temperatura del objeto.
Después de aprender a resolver ecuaciones lineales de primer orden, podrás deducir que
Absorción de glucosa por el cuerpo
El cuerpo absorbe la glucosa a una velocidad proporcional a la cantidad de glucosa presente en el torrente sanguíneo.
Sea λ la constante (positiva) de proporcionalidad. Supongamos que hay G₀ unidades de glucosa en el torrente sanguíneo cuando t = 0, y sea G = G(t) el número de unidades de glucosa en el torrente sanguíneo en el tiempo t > 0.
Entonces, dado que la glucosa que absorbe el cuerpo abandona el torrente sanguíneo, G satisface la ecuación

Del cálculo sabes que si c es alguna constante entonces

satisface la ecuación diferencial (9.1.1_7), y esta función uniparamétrica representa una familia de soluciones, un miembro particular de esta familia para cada valor del parámetro c. Establecer t = 0 en la familia y requerir que G(0) = G₀ produce c = G₀, de donde, en este caso

Ahora vamos a complicar las cosas inyectando glucosa por vía intravenosa a una velocidad constante de r unidades de glucosa por unidad de tiempo.
Entonces, la tasa de cambio de la cantidad de glucosa en el torrente sanguíneo por unidad de tiempo es

donde el primer término a la derecha se debe a la absorción de la glucosa por el cuerpo y el segundo término se debe a la inyección. Más adelante estará capacitado para mostrar que la solución de esta ED (9.1.1_9) que satisface G(0) = G₀ es (Ver la solución dada por ChatGPT)

Los gráficos de esta función son similares a los de la figura 9.1.1_2 (¿Por qué?)
Difusión de epidemias
Un modelo para la propagación de epidemias supone que la cantidad de personas infectadas cambia a un ritmo proporcional al producto de la cantidad de personas ya infectadas y la cantidad de personas que son susceptibles, pero que aún no están infectadas. Por lo tanto, si S denota la población total de personas susceptibles e I = I(t) denota el número de personas infectadas en el momento t, entonces S − I es el número de personas susceptibles, pero aún no infectadas. Así,
donde r es una constante positiva. Suponiendo que I(0) = I₀, la solución de esta ecuación es (Ver la solución dada por ChatGPT)

Los gráficos de esta función son similares a los de la figura 9.1.1_1 (¿Por qué?).
Dado que limt → ∞ I(t) = S, este modelo predice que todas las personas susceptibles se infectarán.
La segunda ley de movimiento de Newton
De acuerdo con la segunda ley de movimiento de Newton, la aceleración instantánea a de un objeto con masa constante m está relacionada con la fuerza F que actúa sobre el objeto mediante la ecuación F = ma. Por simplicidad, supongamos que m = 1 y el movimiento del objeto es a lo largo de una recta vertical. Sea y el desplazamiento del objeto desde algún punto de referencia en la superficie de la Tierra, medido positivo hacia arriba. En muchas aplicaciones, hay tres tipos de fuerzas que pueden actuar sobre el objeto:
(a) Una fuerza como la gravedad que depende solo de la posición y, que escribimos como −p(y), donde p(y) > 0 si y ≥ 0.
(b) Una fuerza como la resistencia atmosférica que depende de la posición y la velocidad del objeto, que escribimos como −q(y, y′)y′, donde q es una función no negativa y hemos puesto y′ “afuera” para indicar que la fuerza resistiva siempre está en la dirección opuesta a la velocidad.
(c) Una fuerza f = f (t), ejercida desde una fuente externa (como una línea de remolque desde un helicóptero) que depende solo de t. En este caso, la segunda ley de Newton implica que que generalmente se reescribe como
que generalmente se reescribe como
Dado que la derivada de segundo orden (y no una superior) de y ocurre en esta ecuación, decimos que es una ecuación diferencial de segundo orden.
Especies que interactúan: Competencia
Supongamos que P = P(t) y Q = Q(t) son las poblaciones de dos especies en el tiempo t, y supongamos que cada población crecería exponencialmente si la otra no existiera; es decir, en ausencia de competencia tendríamos donde a y b son constantes positivas. Una forma de modelar el efecto de la competencia es asumir que la tasa de crecimiento por individuo de cada población se reduce en una cantidad proporcional a la otra población, entonces las dos ecuaciones anteriores se reemplazan por
donde a y b son constantes positivas. Una forma de modelar el efecto de la competencia es asumir que la tasa de crecimiento por individuo de cada población se reduce en una cantidad proporcional a la otra población, entonces las dos ecuaciones anteriores se reemplazan por donde α y β son constantes positivas. (Dado que la población negativa no tiene sentido, este sistema funciona solo mientras P y Q son positivos.) Ahora suponga que P(0) = P₀ > 0 y Q(0) = Q₀ > 0. Se puede mostrar que hay una constante positiva ρ tal que si (P₀, Q₀) está por encima de la recta L a través del origen con pendiente ρ, entonces la especie con población P se extingue en tiempo finito, pero si (P₀, Q₀) está por debajo de L, la especie con población Q se extingue en tiempo finito. La figura 9.1.1_3 ilustra esto. Las curvas que se muestran allí están dadas paramétricamente por P = P(t), Q = Q(t), t > 0. Las flechas indican la dirección a lo largo de las curvas con t creciente.
donde α y β son constantes positivas. (Dado que la población negativa no tiene sentido, este sistema funciona solo mientras P y Q son positivos.) Ahora suponga que P(0) = P₀ > 0 y Q(0) = Q₀ > 0. Se puede mostrar que hay una constante positiva ρ tal que si (P₀, Q₀) está por encima de la recta L a través del origen con pendiente ρ, entonces la especie con población P se extingue en tiempo finito, pero si (P₀, Q₀) está por debajo de L, la especie con población Q se extingue en tiempo finito. La figura 9.1.1_3 ilustra esto. Las curvas que se muestran allí están dadas paramétricamente por P = P(t), Q = Q(t), t > 0. Las flechas indican la dirección a lo largo de las curvas con t creciente.

9.1.2: Conceptos básicos »
