Ejercicios propuestos para el Capítulo 5.11
Exprese la función racional como una suma o diferencia de dos expresiones racionales más simples:
$\frac{1}{(x-3)(x-2)}$
$\frac{x^2 + 1}{x(x+1)(x+2)}$
$\frac{1}{x^3 – x}$
$\frac{3x+1}{x^2}$
$\frac{3x^2}{x^2 + 1}$ (Sugerencia: Use la división larga primero.)
$\frac{2x^4}{x^2 – 2x}$
$\frac{1}{(x-1)(x^2 + 1)}$
$\frac{1}{x^2(x-1)}$
$\frac{x}{x^2 – 4}$
$\frac{1}{x(x-1)(x-2)(x-3)}$
$\frac{1}{x^4 – 1} = \frac{1}{(x+1)(x-1)(x^2+1)}$
$\frac{3x^2}{x^3 – 1} = \frac{3x^2}{(x-1)(x^2+x+1)}$
$\frac{2x}{(x+2)^2}$
$\frac{3x^4 + x^3 + 20x^2 + 3x + 31}{(x+1)(x^2+4)^2}$
Utilice el método de fracciones parciales para evaluar cada una de las siguientes integrales:
$\int \frac{dx}{(x-3)(x-2)}$
$\int \frac{3x}{x^2 + 2x – 8} dx$
$\int \frac{dx}{x^3 – x}$
$\int \frac{x}{x^2 – 4} dx$
$\int \frac{dx}{x(x-1)(x-2)(x-3)}$
$\int \frac{2x^2 + 4x + 22}{x^2 + 2x + 10} dx$
$\int \frac{dx}{x^2 – 5x + 6}$
$\int \frac{2 – x}{x^2 + x} dx$
$\int \frac{2}{x^2 – x – 6} dx$
$\int \frac{dx}{x^3 – 2x^2 – 4x + 8}$
$\int \frac{dx}{x^4 – 10x^2 + 9}$
Evalúe las siguientes integrales, las cuales tienen factores cuadráticos irreducibles:
$\int \frac{2}{(x-4)(x^2 + 2x + 6)} dx$
$\int \frac{x^2}{x^3 – x^2 + 4x – 4} dx$
$\int \frac{x^3 + 6x^2 + 3x + 6}{x^3 + 2x^2} dx$
$\int \frac{x}{(x-1)(x^2 + 2x + 2)^2} dx$
Utilice el método de fracciones parciales para evaluar las siguientes integrales:
$\int \frac{3x + 4}{(x^2 + 4)(3 – x)} dx$
$\int \frac{2}{(x + 2)^2 (2 – x)} dx$
$\int \frac{3x + 4}{x^3 – 2x – 4} dx$ (Sugerencia: Use el teorema de la raíz racional.)
Use la sustitución para convertir las integrales a integrales de funciones racionales. Luego, use fracciones parciales para evaluar las integrales:
$\int_0^1 \frac{e^x}{36 – e^{2x}} dx$ (Dé la respuesta exacta y el equivalente decimal. Redondee a cinco lugares decimales.)
$\int \frac{e^x}{e^{2x} – e^x} dx$
$\int \frac{\sin x}{\sin x – \cos^2 x} dx$
$\int \frac{\sin x}{\cos^2 x + \cos x – 6} dx$
$\int \frac{1 – \sqrt{x}}{1 + \sqrt{x}} dx$
$\int \frac{dt}{(e^t – e^{-t})^2}$
$\int \frac{1 + e^x}{1 – e^x} dx$
$\int \frac{dx}{1 + \sqrt{x} + 1}$
$\int \frac{dx}{\sqrt{x} + \sqrt[4]{x}}$
$\int \frac{\cos x}{\sin x(1 – \sin x)} dx$
$\int \frac{e^x}{(e^{2x} – 4)^2} dx$
$\int_1^2 \frac{1}{x^2 \sqrt{4 – x^2}} dx$
$\int \frac{1}{2 + e^{-x}} dx$
$\int \frac{1}{1 + e^x} dx$
Utilice la sustitución dada para convertir la integral en una integral de una función racional, luego evalúe:
$\int \frac{1}{t – \sqrt[3]{t}} dt = x^3$
$\int \frac{1}{\sqrt{x} + \sqrt[3]{x}} dx ; x = u^6$
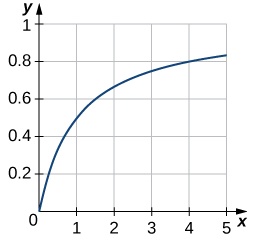
Grafique la curva $y = \frac{x}{1+x}$ sobre el intervalo $[0, 5]$. Luego, encuentre el área de la región limitada por la curva, el eje x, y la línea $x = 4$:
Encuentre el volumen del sólido generado cuando la región limitada por $y = \frac{1}{\sqrt{x(3-x)}}$, $y = 0$, $x = 1$, y $x = 2$ se gira alrededor del eje x.
La velocidad de una partícula que se mueve a lo largo de una línea es una función del tiempo dada por $v(t) = \frac{88t^2}{t^2+1}$. Encuentre la distancia que ha recorrido la partícula después de $t = 5$ segundos.
Resuelva el problema de valor inicial para x como función de t:
$(t^2 – 7t + 12) \frac{dx}{dt} = 1, (t > 4, x(5) = 0)$
$(t + 5) \frac{dx}{dt} = x^2 + 1, t > -5, x(1) = \tan 1$
$(2t^3 – 2t^2 + t – 1) \frac{dx}{dt} = 3, x(2) = 0$
Encuentre la coordenada x del centroide del área limitada por $y(x^2 – 9) = 1$, $y = 0$, $x = 4$, y $x = 5$. (Redondee la respuesta a dos lugares decimales.)
Encuentre el volumen generado al girar el área limitada por $y = \frac{1}{x^3 + 7x^2 + 6x}$, $x = 1$, $x = 7$, y $y = 0$ alrededor del eje y.
Encuentre el área limitada por $y = \frac{x – 12}{x^2 – 8x – 20}$, $y = 0$, $x = 2$, y $x = 4$. (Redondee la respuesta a la centésima más cercana.)
Evalúe la integral $\int \frac{dx}{x^3 + 1}$.
Para los siguientes problemas, use las sustituciones $\tan(\frac{x}{2}) = t$, $dx = \frac{2}{1+t^2} dt$, $\sin x = \frac{2t}{1+t^2}$, y $\cos x = \frac{1-t^2}{1+t^2}$.
$\int \frac{dx}{3 – 5\sin x}$
Encuentre el área bajo la curva $y = \frac{1}{1 + \sin x}$ entre $x = 0$ y $x = \pi$. (Asuma que las dimensiones están en pulgadas.)
Dado $\tan(\frac{x}{2}) = t$, derive las fórmulas $dx = \frac{2}{1+t^2} dt$, $\sin x = \frac{2t}{1+t^2}$, y $\cos x = \frac{1-t^2}{1+t^2}$.
Evalúe $\int \frac{\sqrt[3]{x} – 8}{x} dx$.
