| 4. Aplicaciones de la derivada | Ejercicios propuestos para el Capítulo 4.4 |
4.4 EL TEOREMA DEL VALOR MEDIO
Objetivos de aprendizaje:
4.4.1. Explicar el significado del teorema de Rolle.
4.4.2. Describir la importancia del teorema del valor medio.
4.4.3. Indicar tres consecuencias importantes del teorema del valor medio.
El teorema del valor medio es uno de los teoremas más importantes en el cálculo. Vemos algunas de sus implicaciones al final de esta sección. Primero, comencemos con un caso especial del teorema del valor medio, llamado teorema de Rolle.
El teorema de Rolle
Informalmente, el teorema de Rolle establece que si las salidas de una función diferenciable f son iguales en los puntos finales de un intervalo, entonces debe haber un punto interior c donde f ′(c) = 0. La figura 4.4.1 ilustra este teorema.

Teorema 4.4.1. El teorema de Rolle
Sea f una función continua en el intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b) de modo que f (a) = f (b). Entonces existe al menos un c∈ (a, b) tal que f ′(c) = 0. ♦
Prueba
Sea k = f (a) = f (b). Consideramos tres casos:
- f (x) = k para todo x ∈ (a, b).
- Existe x ∈ (a, b) tal que f (x ) > k.
- Existe x ∈ (a, b) tal que f (x) < k.
Caso 1: Si f (x) = k para todo x ∈ (a, b), entonces f ‘(x) = 0 para todo x ∈ (a, b).
Caso 2: Dado que f es una función continua sobre el intervalo cerrado y acotado [a, b], según el teorema del valor extremo, tiene un máximo absoluto. Además, dado que hay un punto x ∈ (a, b) tal que f (x) > k, el máximo absoluto es mayor que k. Por lo tanto, el máximo absoluto no se produce en ninguno de los puntos finales. Como resultado, el máximo absoluto debe ocurrir en un punto interior c ∈ (a, b). Debido a que f tiene un máximo en un punto interior c, y f es diferenciable en c, por el teorema de Fermat, f ‘(c) = 0.
Caso 3: El caso cuando existe un punto x ∈ (a, b) tal que f (x) < k es análogo al caso 2, con el máximo reemplazado por el mínimo.
Un punto importante sobre el teorema de Rolle es que la diferenciabilidad de la función f es crítica. Si f no es diferenciable, incluso en un solo punto, el resultado puede no ser válido. Por ejemplo, la función f (x) = | x | − 1 es continua sobre [−1, 1] y f (−1) = 0 = f (1), pero f ′(c) ≠ 0 para cualquier c ∈ (−1,1) como se muestra en la siguiente figura.

Figura 4.4.2 Dado que f (x) = | x | − 1 no es diferenciable en x = 0, las condiciones del teorema de Rolle no se cumplen. De hecho, la conclusión no es válida aquí; no hay c ∈ (−1, 1) tal que f ′(c) = 0.
Ejemplo ilustrativo 4.4.1
Para cada una de las siguientes funciones, verifica que la función satisface los criterios establecidos en el teorema de Rolle y encuentra todos los valores \(c\) en el intervalo dado donde \(f'(c) = 0\).
a. \(f(x) = x^2 + 2x\) sobre \([-2, 0]\)
b. \(f(x) = x^3 – 4x\) sobre \([-2, 2]\)
Solución:
a. Dado que \(f\) es un polinomio, es continua y diferenciable en todas partes. Además,
\[ f(-2) = 0 = f(0). \]Por lo tanto, \(f\) satisface los criterios del teorema de Rolle. Concluimos que existe al menos un valor \(c \in (-2, 0)\) tal que \(f'(c) = 0\). Dado que
\[ f'(x) = 2x + 2 = 2(x + 1) \]vemos que \(f'(c) = 2(c + 1) = 0\) implica
\[ c = -1 \]como se muestra en la siguiente gráfica.
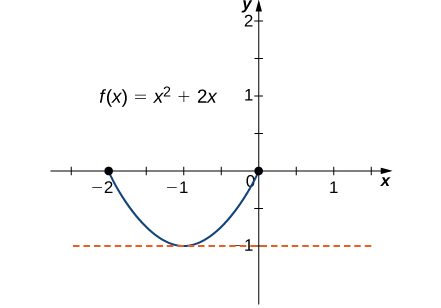
Figura 4.4.3 Esta función es continua y diferenciable sobre \([-2, 0]\), \(f'(c) = 0\) cuando \(c = -1\).
b. Al igual que en la parte a, \(f\) es un polinomio y, por lo tanto, es continua y diferenciable en todas partes. Además,
\[ f(-2) = 0 = f(2). \]Dicho esto, \(f\) satisface los criterios del teorema de Rolle. Derivando, encontramos que
\[ f'(x) = 3x^2 – 4. \]Por lo tanto,
\[ f'(c) = 0 \]cuando
\[ x = \pm\frac{2}{\sqrt{3}}. \]Ambos puntos están en el intervalo \([-2, 2]\) y, por lo tanto, ambos puntos satisfacen la conclusión del teorema de Rolle, como se muestra en la siguiente gráfica.
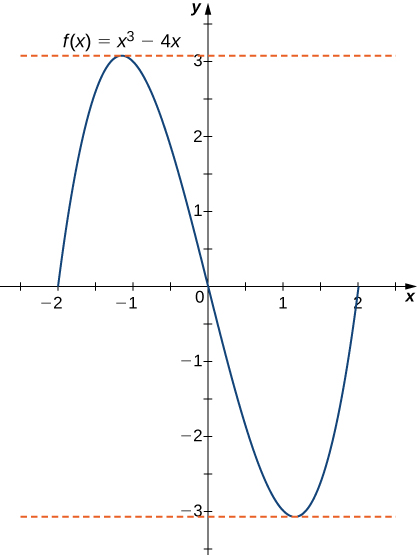
Figura 4.4.4 Para este polinomio sobre \([-2, 2]\), \(f'(c) = 0\) en \(x = \pm\frac{2}{\sqrt{3}}\).
♦
Ejercicio de control 4.4.1
Verifica que la función \(f(x) = 2x^2 – 8x + 6\) definida sobre el intervalo \([1, 3]\) satisface las condiciones del teorema de Rolle. Encuentra todos los puntos \(c\) garantizados por el teorema de Rolle. ♦
El teorema del valor medio y su significado
El teorema de Rolle es un caso especial del teorema del valor medio. En el teorema de Rolle, consideramos funciones diferenciables f definidas en un intervalo cerrado [a, b] con f (a) = f (b). El teorema del valor medio generaliza el teorema de Rolle al considerar funciones que no necesariamente tienen el mismo valor en los puntos finales. En consecuencia, podemos ver el Teorema del valor medio como una versión “inclinada” del teorema de Rolle (Figura 4.4.3). El teorema del valor medio establece que si f es continua durante el intervalo cerrado [a, b] y diferenciable durante el intervalo abierto (a, b), entonces existe un punto c ∈ (a, b) tal que la recta tangente a la gráfica de f en c es paralela a la recta secante que conecta (a, f (a)) y (b, f (b)).

Figura 4.4.5 El teorema del valor medio dice que para una función que cumple sus condiciones, en algún punto la recta tangente tiene la misma pendiente que la recta secante entre los extremos. Para esta función, hay dos valores c1 y c2, de modo que la recta tangente a f en c1 y c2 tiene la misma pendiente que la recta secante.
Teorema 4.4.5. Teorema del valor medio
Sea f continua durante el intervalo cerrado [a, b] y diferenciable durante el intervalo abierto (a, b). Entonces, existe al menos un punto c ∈ (a, b) tal que

Prueba
La prueba se desprende del teorema de Rolle al introducir una función apropiada que satisface los criterios del teorema de Rolle. Considere la recta que conecta (a, f (a)) y (b, f (b)). Como la pendiente de esa recta es

y la recta pasa por el punto (a, f (a)), la ecuación de esa recta se puede escribir como

Supongamos que g (x) denota la diferencia vertical entre el punto (x, f (x)) y el punto (x, y) en esa recta. Por lo tanto,


Figura 4..4.6 El valor g (x) es la diferencia vertical entre el punto (x, f (x)) y el punto (x, y) en la recta secante que conecta (a, f (a)) y (b, f ( b)).
Como la gráfica de f interseca la recta secante cuando x = a y x = b, vemos que g (a) = 0 = g (b). Dado que f es una función diferenciable sobre (a, b), g también es una función diferenciable sobre (a, b). Además, dado que f es continua sobre [a, b], g también es continua sobre [a, b]. Por lo tanto, g satisface los criterios del teorema de Rolle. En consecuencia, existe un punto c ∈ (a, b) tal que g ′(c) = 0. Ya que

vemos que

Como g ‘(c) = 0, concluimos que

Una aplicación que ayuda a ilustrar el teorema del valor medio implica la velocidad. Por ejemplo, supongamos que conducimos un automóvil durante 1 h por una carretera recta con una velocidad promedio de 45 mph. Supongamos que s (t) y v (t) denotan la posición y la velocidad del automóvil, respectivamente, para 0 ≤ t ≤ 1 h. Suponiendo que la función de posición s (t) es diferenciable, podemos aplicar el teorema del valor medio para concluir que, en algún momento c ∈ (0,1), la velocidad del automóvil era exactamente

Ejemplo ilustrativo 4.4.2
Para \(f(x) = \sqrt{x}\) sobre el intervalo \([0, 9]\), muestra que \(f\) satisface las hipótesis del Teorema del Valor Medio y, por lo tanto, existe al menos un valor \(c \in (0, 9)\) tal que \(f'(c)\) es igual a la pendiente de la recta que conecta \((0, f(0))\) y \((9, f(9))\). Encuentra estos valores \(c\) garantizados por el Teorema del Valor Medio.
Solución:
Sabemos que \(f(x) = \sqrt{x}\) es continua sobre \([0, 9]\) y diferenciable sobre \((0, 9)\). Por lo tanto, \(f\) satisface las hipótesis del Teorema del Valor Medio, y debe existir al menos un valor \(c \in (0, 9)\) tal que \(f'(c)\) es igual a la pendiente de la recta que conecta \((0, f(0))\) y \((9, f(9))\) (Figura 4.4.7). Para determinar qué valor(es) de \(c\) están garantizados, primero calculamos la derivada de \(f\). La derivada es
\[ f'(x) = \frac{1}{2\sqrt{x}}. \]La pendiente de la recta que conecta \((0, f(0))\) y \((9, f(9))\) está dada por
\[ \frac{f(9) – f(0)}{9 – 0} = \frac{\sqrt{9} – \sqrt{0}}{9 – 0} = \frac{3}{9} = \frac{1}{3}. \]Queremos encontrar \(c\) tal que
\[ f'(c) = \frac{1}{3}. \]Es decir, queremos encontrar \(c\) tal que
\[ \frac{1}{2\sqrt{c}} = \frac{1}{3}. \]Resolviendo esta ecuación para \(c\), obtenemos
\[ c = \frac{9}{4}. \]En este punto, la pendiente de la recta tangente es igual a la pendiente de la recta que une los puntos extremos.
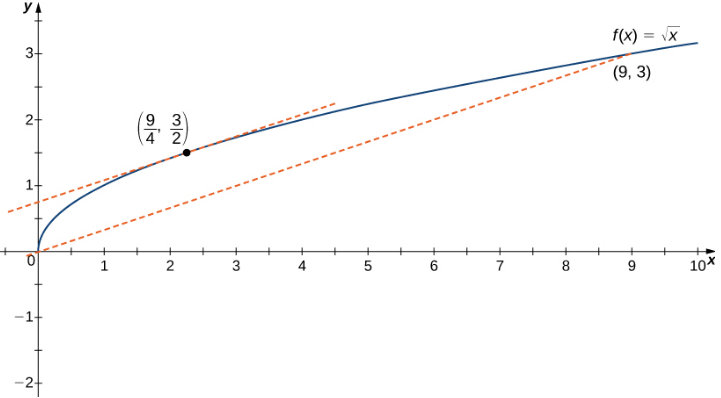
Figura 4.4.7 La pendiente de la recta tangente en c = 9/4 es la misma que la pendiente del segmento de recta que conecta (0, 0) y (9, 3).
Una aplicación que ayuda a ilustrar el Teorema del Valor Medio involucra la velocidad. Por ejemplo, supongamos que conducimos un automóvil durante 1 h por una carretera recta con una velocidad promedio de 45 mph. Sean \(s(t)\) y \(v(t)\) la posición y la velocidad del automóvil, respectivamente, para \(0 \le t \le 1\) h. Asumiendo que la función de posición \(s(t)\) es diferenciable, podemos aplicar el Teorema del Valor Medio para concluir que, en algún tiempo \(c \in (0, 1)\), la velocidad del automóvil fue exactamente
\[ v(c) = s'(c) = \frac{s(1) – s(0)}{1 – 0} = 45 \text{ mph}. \]♦
Ejemplo ilustrativo 4.4.3
Si se deja caer una roca desde una altura de 100 pies, su posición \(t\) segundos después de que se suelta hasta que toca el suelo está dada por la función \(s(t) = -16t^2 + 100\).
a. Determina cuánto tiempo tarda la roca en tocar el suelo.
b. Encuentra la velocidad promedio \(v_{avg}\) de la roca desde que se suelta hasta que toca el suelo.
c. Encuentra el tiempo \(t\) garantizado por el Teorema del Valor Medio cuando la velocidad instantánea de la roca es \(v_{avg}\).
Solución:
a. Cuando la roca toca el suelo, su posición es \(s(t) = 0\), resolviendo \(-16t^2 + 100 = 0\) para \(t\), encontramos \(t = \pm\frac{5}{2}\) seg; como \(t \ge 0\), la roca toca el suelo \(\frac{5}{2}\) seg después de ser soltada.
b. La velocidad promedio está dada por
\[ v_{avg} = \frac{s(5/2) – s(0)}{5/2 – 0} = \frac{0 – 100}{5/2} = -40 \text{ ft/seg}. \]c. La velocidad instantánea está dada por la derivada de la función de posición. Por lo tanto, necesitamos encontrar un tiempo \(t\) tal que \(v(t) = s'(t) = v_{avg} = -40 \text{ ft/seg}\). Dado que \(s(t)\) es continua sobre el intervalo \([0, 5/2]\) y diferenciable sobre el intervalo \((0, 5/2)\), por el Teorema del Valor Medio, se garantiza que existe un punto \(c \in (0, 5/2)\) tal que
\[ s'(c) = \frac{s(5/2) – s(0)}{5/2 – 0} = -40. \]Tomando la derivada de la función de posición \(s(t)\), encontramos que \(s'(t) = -32t\). Por lo tanto, la ecuación se reduce a \(s'(c) = -32c = -40\). Resolviendo esta ecuación para \(c\), tenemos
\[ c = \frac{5}{4}. \]Por lo tanto, \(\frac{5}{4}\) seg después de que se suelta la roca, la velocidad instantánea es igual a la velocidad promedio de la roca durante su caída libre: -40 ft/seg.
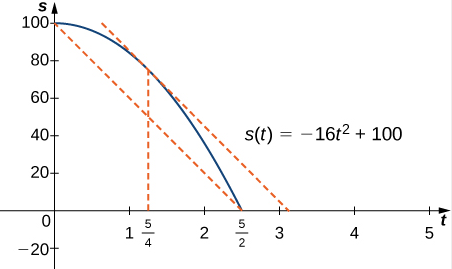
Figura 4.4.8 En el tiempo t = 5/4 segundos, la velocidad de la roca es igual a su velocidad promedio desde el momento en que se suelta hasta que golpea el suelo.
♦
Ejercicio de control 4.4.2
Supongamos que se deja caer una bola desde una altura de 200 pies. Su posición en el tiempo \(t\) está dada por \(s(t) = -16t^2 + 200\). Encuentra el tiempo \(t\) cuando la velocidad instantánea de la bola es igual a su velocidad promedio. ♦
Corolarios del teorema del valor medio
Veamos ahora tres corolarios del teorema del valor medio. Estos resultados tienen consecuencias importantes, que usaremos en las próximas secciones.
En este punto, sabemos que la derivada de cualquier función constante es cero. El teorema del valor medio nos permite concluir que lo contrario también es cierto. En particular, si f ′ (x) = 0 para todas las x en algún intervalo I, entonces f (x) es constante durante ese intervalo. Este resultado puede parecer intuitivamente obvio, pero tiene implicaciones importantes que no son obvias, y lo discutiremos en breve.
Teorema 4.4.6. Corolario 1: Funciones con una derivada de cero
Sea f diferenciable en un intervalo I. Si f ′ (x) = 0 para todo x ∈ I, entonces f (x) = constante para todo x ∈ I. ♦
Prueba
Dado que f es diferenciable sobre I, f debe ser continua sobre I. Suponga que f (x) no es constante para todas las x en I. Entonces existen a, b ∈ I, donde a ≠ b y f (a) ≠ f (b ) Elija la notación para que a < b. Por lo tanto,

Dado que f es una función diferenciable, según el teorema del valor medio, existe c ∈ (a, b) tal que

Por lo tanto, existe c ∈ I tal que f ′ (c) ≠ 0, lo que contradice la suposición de que f ′ (x) = 0 para todo x ∈ I.
Del Corolario 1: Funciones con una derivada de cero, se deduce que si dos funciones tienen la misma derivada, difieren en, como máximo, una constante.
Teorema 4.4.7. Corolario 2: Teorema de la diferencia constante
Si f y g son diferenciables en un intervalo I y f ′ (x) = g ′ (x) para todo x ∈ I, entonces f (x) = g (x) + C para alguna constante C. ♦
Prueba
Sea h (x) = f (x) − g (x). Entonces, h ′ (x) = f ′ (x) − g ′ (x) = 0 para todo x ∈ I. Según el Corolario 1, hay una constante C tal que h (x) = C para todo x ∈ I. Por lo tanto, f (x) = g (x) + C para todo x ∈ I.
El tercer corolario del teorema del valor medio analiza cuándo una función está creciendo y cuándo está decreciendo. Recuerde que una función f es creciente sobre I si f (x1) < f (x2) siempre que x1 < x2, mientras que f decrece sobre I si f (x1) > f (x2) cuando x1 < x2. Usando el teorema del valor medio, podemos mostrar que si la derivada de una función es positiva, entonces la función está aumentando; Si la derivada es negativa, entonces la función está disminuyendo (Figura 4.15). Hacemos uso de este hecho en la siguiente sección, donde mostramos cómo usar la derivada de una función para localizar los valores máximos y mínimos locales de la función, y cómo determinar la forma de la gráfica.
Este hecho es importante porque significa que para una función dada f, si existe una función F tal que F ‘(x) = f (x); entonces, las únicas otras funciones que tienen una derivada igual a f son F (x) + C para alguna constante C. Discutiremos este resultado con más detalle más adelante en el capítulo.

Teorema 4.4.8. Corolario 3: Funciones crecientes y decrecientes
Sea \(f\) continua sobre el intervalo cerrado \([a, b]\) y diferenciable sobre el intervalo abierto \((a, b)\).
i. Si \(f'(x) > 0\) para toda \(x \in (a, b)\), entonces \(f\) es una función creciente sobre \([a, b]\).
ii. Si \(f'(x) < 0\) para toda \(x \in (a, b)\), entonces \(f\) es una función decreciente sobre \([a, b]\).
♦
Prueba
Nosotros demostraremos (i); la prueba de (ii) es similar. Suponga que f no es una función creciente en I. Entonces existen a y b en I de modo que a < b, pero f (a) ≥ f (b). Dado que f es una función diferenciable sobre I, por el teorema del valor medio existe c ∈ (a, b) tal que

Como f (a) ≥ f (b), sabemos que f (b) − f (a) ≤ 0. Además, a < b nos dice que b − a > 0. Concluimos que

