| 3. La derivada | Ejercicios propuestos de la sección 3.9 |

3.9 Derivadas de funciones exponenciales y logarítmicas

Objetivos de aprendizaje:

3.9.1. Encuentra la derivada de funciones exponenciales.
3.9.2. Encuentra la derivada de las funciones logarítmicas.
3.9.3. Use la diferenciación logarítmica para determinar la derivada de una función.

    Hasta ahora, hemos aprendido a diferenciar una variedad de funciones, incluidas las funciones trigonométricas, inversas e implícitas. En esta sección, exploramos derivadas de funciones exponenciales y logarítmicas. Como discutimos en Introducción a las funciones y sus gráficas, las funciones exponenciales juegan un papel importante en el modelado del crecimiento de la población y la descomposición de los materiales radiactivos. Las funciones logarítmicas pueden ayudar a reescalar grandes cantidades y son particularmente útiles para reescribir expresiones complicadas.

Derivada de la función exponencial

Al igual que cuando encontramos las derivadas de otras funciones, podemos encontrar las derivadas de funciones exponenciales y logarítmicas utilizando fórmulas. A medida que desarrollamos estas fórmulas, necesitamos hacer ciertas suposiciones básicas. Las pruebas que sostienen estos supuestos están más allá del alcance de este curso.

Primero que nada, comenzamos con la suposición de que la función \(B(x) = b^x\), \(b > 0\), está definida para todo número real y es continua. En cursos anteriores, los valores de las funciones exponenciales para todos los números racionales fueron definidos—comenzando con la definición de \(b^n\), donde \(n\) es un entero positivo—como el producto de \(b\) multiplicado por sí mismo \(n\) veces. Más tarde, definimos \(b^0 = 1\), \(b^{-n} = \frac{1}{b^n}\), para un entero positivo \(n\), y \(b^{s/t} = (\sqrt[t]{b})^s\) para enteros positivos \(s\) y \(t\).

Estas definiciones dejan abierta la cuestión del valor de \(b^r\) donde \(r\) es un número real arbitrario. Al asumir la continuidad de \(B(x) = b^x\), \(b > 0\), podemos interpretar \(b^r\) como \(\lim_{x \to r} b^x\) donde los valores de \(x\) al tomar el límite son racionales. Por ejemplo, podemos ver \(4^\pi\) como el número que satisface

\[ 4^3 < 4^\pi < 4^4, \quad 4^{3.1} < 4^\pi < 4^{3.2}, \quad 4^{3.14} < 4^\pi < 4^{3.15}, \\ 4^{3.141} < 4^\pi < 4^{3.142}, \quad 4^{3.1415} < 4^\pi < 4^{3.1416}, \quad \dots \]

Como vemos en la siguiente tabla, 4^π ≈ 77.88.

También suponemos que para B(x) = b^x, b > 0, existe el valor B′(0) de la derivada. En esta sección, mostramos que al hacer esta suposición adicional, es posible demostrar que la función B(x) es diferenciable en todas partes.

Hacemos una suposición final: que hay un valor único de b > 0 para el cual B′(0) = 1. Definimos e como este valor único, como lo hicimos en Introducción a funciones y sus gráficas. La figura 3.9_1 proporciona gráficas de las funciones y = 2^x, y = 3^x, y = 2.7^x, y y = 2.8^x. Una estimación visual de las pendientes de las rectas tangentes a estas funciones en 0 proporciona evidencia de que el valor de e se encuentra entre 2.7 y 2.8. La función E(x) = e^x se llama función exponencial natural. Su inverso, L(x) = log_ex = lnx se llama función logaritmo natural.

Para una mejor estimación de e, podemos construir una tabla de estimaciones de B′(0) para funciones de la forma B(x) = bˣ. Antes de hacer esto, recuerda que

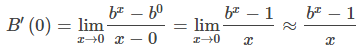
para valores de x muy cercanos a cero. Para nuestras estimaciones, elegimos x = 0.00001 y x = −0.00001 para obtener la estimación

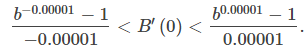
Ver la siguiente tabla:

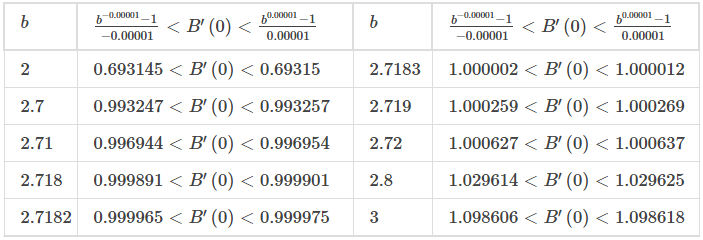
La evidencia de la tabla sugiere que 2.7182 < e < 2.7183.

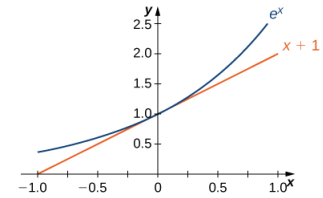
La gráfica de E(x) = eˣ junto con la recta y = x + 1 se muestran en la Figura 3.9_2 Esta recta es tangente a la gráfica de E(x) = eˣ en x = 0.

       Ahora que hemos presentado nuestras suposiciones básicas, comenzamos nuestra investigación explorando la derivada de B(x) = bˣ, b > 0. Recordemos que hemos asumido que B′(0) existe. Al aplicar la definición por límite de la derivada, concluimos que

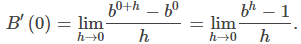
Pasando a \(B'(x)\), obtenemos lo siguiente:

\[ \begin{aligned} B'(x) &= \lim_{h \to 0} \frac{b^{x+h} – b^x}{h} & \text{Aplicar la definición de límite de la derivada.} \\ &= \lim_{h \to 0} \frac{b^x b^h – b^x}{h} & \text{Nótese que } b^{x+h} = b^x b^h. \\ &= \lim_{h \to 0} \frac{b^x(b^h – 1)}{h} & \text{Factorizar } b^x. \\ &= b^x \lim_{h \to 0} \frac{b^h – 1}{h} & \text{Aplicar una propiedad de los límites.} \\ &= b^x B'(0) & \text{Usar } B'(0) = \lim_{h \to 0} \frac{b^{0+h} – b^0}{h} = \lim_{h \to 0} \frac{b^h – 1}{h}. \end{aligned} \]

Vemos que, sobre la base de la suposición de que \(B(x) = b^x\) es diferenciable en 0, \(B(x)\) no solo es diferenciable en todas partes, sino que su derivada es

\[ B'(x) = b^x B'(0). \]

Para E(x) = eˣ, E′(0) = 1. Por lo tanto, tenemos E′(x) = eˣ. (El valor de B′(0) para una función arbitraria de la forma B(x) = bˣ, b > 0, se deducirá más adelante).

TEOREMA 3.9.1. Derivada de la función exponencial natural

Sea \(E(x) = e^x\) la función exponencial natural. Entonces,

\[ E'(x) = e^x. \]

En general,

\[ \frac{d}{dx}(e^{g(x)}) = e^{g(x)} g'(x). \]

♦

Ejemplo ilustrativo 3.9_1. Derivada de una función exponencial

Encuentra la derivada deSolución:

Usando la fórmula para la derivada de una función exponencial natural y la regla de la cadena, se obtiene:

♦

Ejemplo ilustrativo 3.9_2. Combinación de reglas de diferenciación

Encuentra la derivada de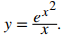

Solución:
Use la derivada de la función exponencial natural, la regla del cociente y la regla de la cadena:♦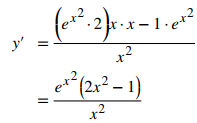  

Ejercicio de control 3.9.1

Encuentra la derivada de \(h(x) = xe^{2x}\). ♦

Ejemplo ilustrativo 3.9_3. Aplicando la función exponencial natural

Una colonia de mosquitos tiene una población inicial de 1000 individuos. Después de t días, la población viene dada por A(t) = 1000e⁰·³ᵗ. Demuestre que la razón de la tasa de cambio de la población, A′(t), a la población, A(t), es constante.

Solución:
Primero encuentre A′(t). Al usar la regla de la cadena, tenemos A′(t) = 300e⁰·³ᵗ. Por lo tanto, la razón de la tasa de cambio de la población a la población viene dada por

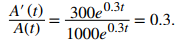
La razón de la tasa de cambio de la población a la población es la constante 0.3. ♦

Ejercicio de control 3.9.2

Si \(A(t) = 1000e^{0.3t}\) describe la población de mosquitos después de \(t\) días, como en el ejemplo anterior, ¿cuál es la tasa de cambio de \(A(t)\) después de 4 días? ♦

Derivada de la función logarítmica

Ahora que tenemos la derivada de la función exponencial natural, podemos usar la diferenciación implícita para encontrar la derivada de su función inversa, la función logarítmica natural .

TEOREMA 3.9.2. La derivada de la función logarítmica natural

Si \(x > 0\) e \(y = \ln x\), entonces

\[ \frac{dy}{dx} = \frac{1}{x} \]

De manera más general, sea \(g(x)\) una función diferenciable. Para todos los valores de \(x\) para los cuales \(g'(x) > 0\), la derivada de \(h(x) = \ln(g(x))\) está dada por

\[ h'(x) = \frac{1}{g(x)} g'(x). \]

♦

Prueba:

Si x > 0 e y = lnx, entonces eʸ = x. Diferenciar ambos lados de esta ecuación da como resultado la ecuaciónDespejamos dy/dxFinalmente, sustituimos x = eʸ para obtener

También podemos derivar este resultado aplicando el teorema de la función inversa, como sigue. Dado que y = g(x) = lnx es la inversa de f (x) = eˣ, aplicando el teorema de la función inversa tenemos

Usando este resultado y aplicando la regla de la cadena a h(x) = ln(g(x)) se obtiene♦

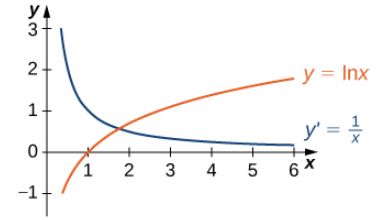
La gráfica de y = lnx y su derivada dy/dx = 1/x se muestran en la figura 3.9_3.

Ejemplo ilustrativo 3.9_4. Tomando una derivada de un logaritmo natural

Encuentre la derivada de f (x) = ln (x³ + 3x − 4).

Solución:
Use directamente la ecuación

♦

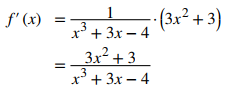
Ejemplo ilustrativo 3.9_5. Uso de las propiedades de los logaritmos en una derivada

Encuentra la derivada de

Solución:

A primera vista, tomar esta derivada parece bastante complicado. Sin embargo, al usar las propiedades de los logaritmos antes de empezar a calcular la derivada, podemos simplificar el problema:

♦

Ejercicio de control 3.9.3

Diferenciar: \(f(x) = \ln(3x + 2)^5\). ♦

       Ahora que podemos diferenciar la función logarítmica natural, podemos usar este resultado para encontrar las derivadas de y = log_bx e y = b^x para b > 0, b ≠ 1.

TEOREMA 3.9.3. Derivadas de funciones exponenciales y logarítmicas generales

Sea \(b > 0\), \(b \ne 1\), y sea \(g(x)\) una función diferenciable.

i. Si \(y = \log_b x\), entonces

\[ \frac{dy}{dx} = \frac{1}{x \ln b}. \]

De manera más general, si \(h(x) = \log_b(g(x))\), entonces para todos los valores de \(x\) para los cuales \(g(x) > 0\),

\[ h'(x) = \frac{g'(x)}{g(x) \ln b}. \]

ii. Si \(y = b^x\), entonces

\[ \frac{dy}{dx} = b^x \ln b. \]

De manera más general, si \(h(x) = b^{g(x)}\), entonces

\[ h'(x) = b^{g(x)} g'(x) \ln b. \]

♦

Prueba

Si \(y = \log_b x\), entonces \(b^y = x\). Se deduce que \(\ln(b^y) = \ln x\). Así, \(y \ln b = \ln x\). Resolviendo para \(y\), tenemos \(y = \frac{\ln x}{\ln b}\). Al diferenciar y tener en cuenta que \(\ln b\) es una constante, vemos que

\[ \frac{dy}{dx} = \frac{1}{x \ln b}. \]

La derivada en la ecuación

\[ h'(x) = \frac{g'(x)}{g(x) \ln b} \]

ahora se sigue de la regla de la cadena.

Si \(y = b^x\), entonces \(\ln y = x \ln b\). Usando la diferenciación implícita, nuevamente teniendo en cuenta que \(\ln b\) es constante, se deduce que \(\frac{1}{y} \frac{dy}{dx} = \ln b\). Resolviendo \(\frac{dy}{dx}\) y sustituyendo \(y = b^x\), vemos que

\[ \frac{dy}{dx} = y \ln b = b^x \ln b. \]

La derivada más general

\[ h'(x) = b^{g(x)} g'(x) \ln b. \]

se deduce de la regla de la cadena. \(\Box\)

Ejemplo ilustrativo 3.9_6. Aplicación de fórmulas de derivadas

Encuentra la derivada de

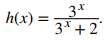
Solución:
Use la regla del cociente y las reglas para las derivadas de las funciones exponenciales y logarítmicas generales.

♦

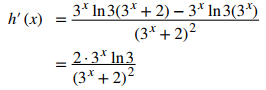
Ejemplo ilustrativo 3.9_7. Encontrar la pendiente de una recta tangente

Encuentre la pendiente de la recta tangente a la gráfica de y = log₂ (3x + 1) en x = 1.

Solución:
Para encontrar la pendiente, debemos evaluar dy/dx en x = 1. Usando la ecuación

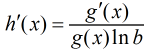
, vemos que

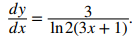
Al evaluar la derivada en x = 1, vemos que la recta tangente tiene pendiente

♦

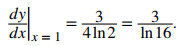
Ejercicio de control 3.9.4

Encuentra la pendiente de la recta tangente a \(y = 3^x\) en \(x = 2\). ♦

Diferenciación logarítmica

En este punto, podemos tomar derivadas de funciones de la forma y = (g(x))ⁿ para ciertos valores de n, así como funciones de la forma y = bᵍ⁽ˣ⁾, donde b > 0 y b ≠ 1 . Desafortunadamente, todavía no conocemos las derivadas de funciones como

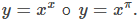
Estas funciones requieren una técnica llamada diferenciación logarítmica, que nos permite diferenciar cualquier función de la forma h(x) = g(x)ᶠ⁽ˣ⁾. También se puede usar para convertir un problema de diferenciación muy complejo en uno más simple, como encontrar la derivada de

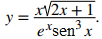
Esbozamos esta técnica en la siguiente estrategia de resolución de problemas.

ESTRATEGIA PARA RESOLVER PROBLEMAS: UTILIZAR LA DIFERENCIACIÓN LOGARÍTMICA

1. Para diferenciar y = h(x) usando la diferenciación logarítmica, tome el logaritmo natural de ambos lados de la ecuación para obtener lny = ln(h(x)).
2. Use las propiedades de los logaritmos para expandir ln (h (x)) tanto como sea posible.
3. Diferenciar ambos lados de la ecuación. A la izquierda tendremos (1/y)(dy/dx).
4. Multiplica ambos lados de la ecuación por y para despejar dy/dx
5. Reemplace y por h(x). ♦

Ejemplo ilustrativo 3.9_8. Usando la diferenciación logarítmica

Halle la derivada de

Solución:
Use la diferenciación logarítmica para encontrar esta derivada:

♦

Ejemplo ilustrativo 3.9_9. Usando la diferenciación logarítmica

Encuentra la derivada deSolución:
Este problema realmente hace uso de las propiedades de los logaritmos y las reglas de diferenciación dadas en este capítulo.

♦

Ejemplo ilustrativo 3.9_10. Extendiendo la Regla de la Potencia

Encuentre la derivada de y = xʳ donde r es un número real arbitrario.

Solución:

El proceso es el mismo que en el Ejemplo 3.9_9, aunque con menos complicaciones.

♦

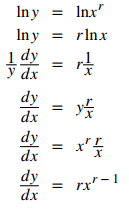
Ejercicio de control 3.9.5

Usa la diferenciación logarítmica para encontrar la derivada de \(y = x^x\). ♦

Ejercicio de control 3.9.6

Encuentra la derivada de \(y = (\tan x)^\pi\). ♦