| 6. Aplicaciones de la integral | Ejercicios propuestos para el Capítulo 6.2 |

6.2 Determinación de volúmenes por rebanadas

Objetivos de aprendizaje:

6.2.1. Determine el volumen de un sólido integrando una sección transversal (el método de rebanado).
6.2.2. Encontrar el volumen de un sólido de revolución usando el método del disco.
6.2.3. Encontrar el volumen de un sólido de revolución con una cavidad utilizando el método de arandelas.

En la sección anterior, usamos integrales definidas para encontrar el área entre dos curvas. En esta sección, usamos integrales definidas para encontrar volúmenes de sólidos tridimensionales. Consideramos tres enfoques (corte, discos y arandelas) para encontrar estos volúmenes, dependiendo de las características del sólido.

Volumen y el método de corte (rebanadas)

Así como el área es la medida numérica de una región bidimensional, el volumen es la medida numérica de un sólido tridimensional. La mayoría de nosotros hemos calculado volúmenes de sólidos usando fórmulas geométricas básicas. El volumen de un sólido rectangular, por ejemplo, se puede calcular multiplicando la longitud, el ancho y la altura: V = lwh.

Las fórmulas para el volumen de una esfera

un cono

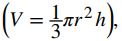
y una pirámide

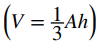
También se han introducido. Aunque algunas de estas fórmulas se obtuvieron usando solo geometría, todas estas fórmulas se pueden obtener mediante la integración.

El cilindro

También podemos calcular el volumen de un cilindro. Aunque la mayoría de nosotros pensamos que un cilindro tiene una base circular, como una lata de sopa o una varilla de metal, en matemáticas la palabra cilindro tiene un significado más general. Para discutir los cilindros en este contexto más general, primero necesitamos definir algo de vocabulario.

Definimos la sección transversal de un sólido como la intersección de un plano con el sólido.

Un cilindro se define como cualquier sólido que se pueda generar por traslación de una región plana a lo largo de una línea perpendicular a la región, llamada eje del cilindro. Por lo tanto, todas las secciones transversales perpendiculares al eje de un cilindro son idénticas. El sólido que se muestra en la figura 6.2.1 es un ejemplo de un cilindro con una base no circular. Para calcular el volumen de un cilindro, simplemente multiplicamos el área A de la sección transversal por la altura h del cilindro: V = A⋅ h. En el caso de un cilindro circular recto (lata de sopa), esto se convierte en

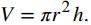
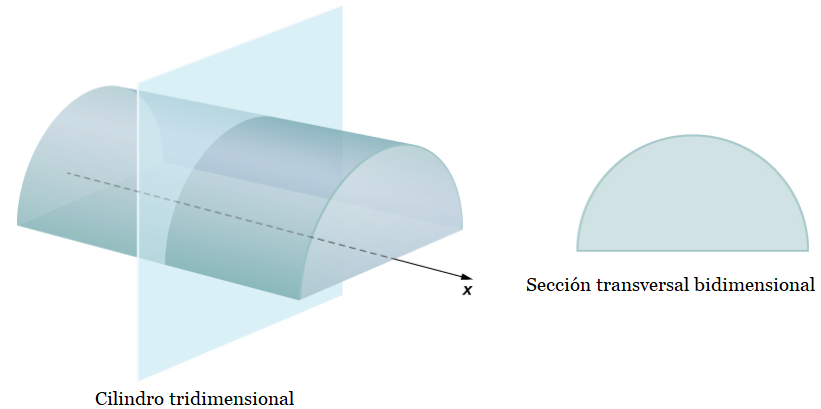
Figura 6.2.1   Cada sección transversal de un cilindro particular es idéntica a las demás.

---

Si un sólido no tiene una sección transversal constante (y no es uno de los otros sólidos básicos), es posible que no tengamos una fórmula para su volumen. En este caso, podemos usar una integral definida para calcular el volumen del sólido. Hacemos esto cortando el sólido en trozos, estimando el volumen de cada rebanada y luego sumando esos volúmenes estimados. Todas las rebanadas deben ser paralelas entre sí, y cuando juntamos todas las rebanadas, deberíamos obtener todo el sólido. Considere, por ejemplo, el sólido S que se muestra en la Figura 6.2.2, que se extiende a lo largo del eje x.

Queremos dividir el sólido S en rodajas perpendiculares al eje x. Como veremos más adelante en el capítulo, puede haber momentos en los que queramos cortar el sólido en otra dirección, por ejemplo, con cortes perpendiculares al eje y. La decisión de qué manera cortar el sólido es muy importante. Si tomamos la decisión equivocada, los cálculos pueden volverse bastante desordenados. Más adelante en el capítulo, examinamos algunas de estas situaciones en detalle y observamos cómo decidir de qué manera cortar el sólido. Para los propósitos de esta sección, sin embargo, usamos cortes perpendiculares al eje x.

Debido a que el área de la sección transversal no es constante, dejamos que A(x) represente el área de la sección transversal en el punto x. Ahora dejemos que P = {x₀, x₁ …, x_n} sea una partición regular del intervalo cerrado [a, b], y para i = 1, 2, … n, dejemos que S_i represente la porción de S que se extiende desde x_{i − 1} a x_i. La siguiente figura muestra el sólido en rodajas con n = 3.

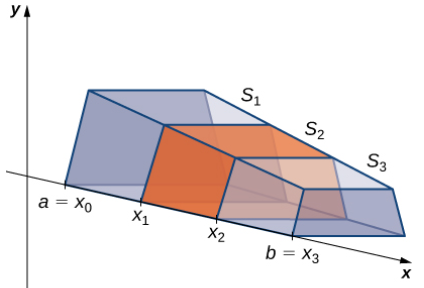
Finalmente, para i = 1, 2, … n, sea x_i* un punto arbitrario en [x_{i − 1}, x_i]. Entonces, el volumen del segmento S_i puede estimarse por V(S_i) ≈ A(x_i*)Δx. Sumando estas aproximaciones juntas, vemos que el volumen de todo el sólido S puede aproximarse por

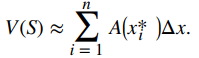
Por ahora, podemos reconocer esto como una suma de Riemann, y nuestro siguiente paso es tomar el límite cuando  n → ∞. Entonces tenemos

La técnica que acabamos de describir se llama método de rebanado. Para aplicarlo, utilizamos la siguiente estrategia.

Estrategia para resolver problemas: Encontrar volúmenes por el método de REBANADO

1. Examine el sólido y determine la forma de una sección transversal del sólido. A menudo es útil hacer un dibujo si no se proporciona uno.
2. Determine una fórmula para el área de la sección transversal.
3. Integre la fórmula del área sobre el intervalo apropiado para obtener el volumen. ♦

Recuerde que en esta sección, asumimos que los cortes son perpendiculares al eje x. Por lo tanto, la fórmula del área está en términos de x y los límites de integración se encuentran en el eje x. Sin embargo, la estrategia de resolución de problemas que se muestra aquí es válida independientemente de cómo elijamos cortar el sólido.

EJEMPLO ILUSTRATIVO 6.2_1.  Derivando la fórmula para el volumen de una pirámide

Sabemos por la geometría que la fórmula para el volumen de una pirámide es V = (1/3)Ah. Si la pirámide tiene una base cuadrada, esto se convierte en V = (1/3)a²h, donde a denota la longitud de un lado de la base. Usaremos el método de corte para derivar esta fórmula.

Solución:

Queremos aplicar el método de corte a una pirámide con una base cuadrada. Para configurar la integral, considere la pirámide que se muestra en la Figura 6.6, orientada a lo largo del eje x.

(Figura 6.2.4 (a) Una pirámide con una base cuadrada está orientada a lo largo del eje x. (b) Una vista bidimensional de la pirámide se ve de lado.)

Primero queremos determinar la forma de una sección transversal de la pirámide. Sabemos que la base es un cuadrado, por lo que las secciones transversales también son cuadrados (paso 1). Ahora queremos determinar una fórmula para el área de uno de estos cuadrados transversales. Mirando la Figura 6.2.4 (b), y usando una proporción, dado que estos son triángulos semejantes, tenemos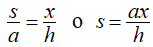

Por lo tanto, el área de uno de los cuadrados de sección transversal es

Luego encontramos el volumen de la pirámide integrando de 0 a h (paso 3):

Esta es la fórmula que estábamos buscando. ♦

Ejercicio de control 6.2_1

Utilice el método de corte para obtener la fórmula V = (1/3)πr²h para el volumen de un cono circular. ♦

Sólidos de revolución

Si una región en un plano gira alrededor de una recta en ese plano, el sólido resultante se llama sólido de revolución, como se muestra en la siguiente figura.

EJEMPLO ILUSTRATIVO 6.2_2. Usando el método de rebanar para encontrar el volumen de un sólido de revolución

Utilice el método de corte para hallar el volumen del sólido de revolución acotado por las gráficas de f (x) = x² − 4x + 5, x = 1 y x = 4, y rotado sobre el eje x.

Solución:
Usando la estrategia de resolución de problemas, primero dibujamos la gráfica de la función cuadrática sobre el intervalo [1, 4] como se muestra en la siguiente figura.

(Figura 6.2.6 Una región utilizada para producir un sólido de revolución).

 

A continuación, gire la región alrededor del eje x, como se muestra en la siguiente figura.

(Figura 6.2.7 Dos vistas, (a) y (b), del sólido de revolución producido al girar la región de la Figura 6.2_7 alrededor del eje x).

 

Dado que el sólido se formó girando la región alrededor del eje x, las secciones transversales son círculos (paso 1). El área de la sección transversal, entonces, es el área de un círculo, y el radio del círculo está dado por f (x). Usa la fórmula para el área del círculo:

A(x) = πr² = π[ f (x)]² = π(x² − 4x + 5)²                     (paso 2).

El volumen, entonces, es (paso 3)

El volumen es 78π/5 de unidades cúbicas. ♦

Ejercicio de control 6.2_2

Utilice el método de corte para encontrar el volumen del sólido de revolución formado al hacer girar la región entre la gráfica de la función f (x) = 1/x y el eje x sobre el intervalo [1, 2] alrededor del eje x. Vea la siguiente figura. 

Figura 2.6.8

♦

El método del disco

Cuando usamos el método de rebanadas con sólidos de revolución, a menudo se le llama método del disco porque, para los sólidos de revolución, las rebanadas que se usan para aproximar el volumen del sólido son discos. Para ver esto, considere el sólido de revolución generado al girar la región entre la gráfica de la función

y el eje x sobre el intervalo [−1, 3] alrededor del eje-x. La gráfica de la función y un disco representativo se muestran en la Figura 6.7 (a) y (b). La región de revolución y el sólido resultante se muestran en la Figura 6.7 (c) y (d).

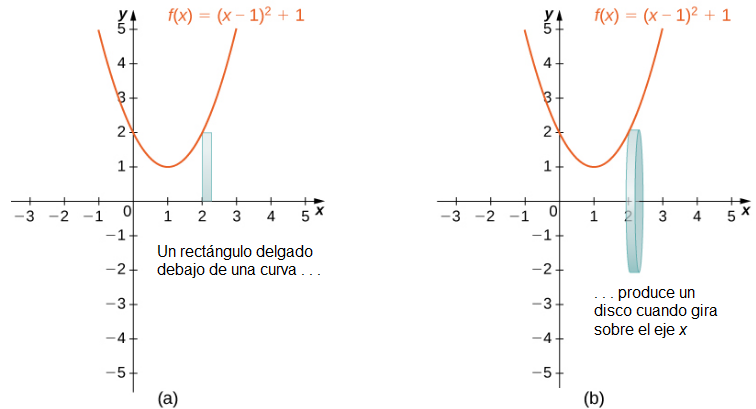
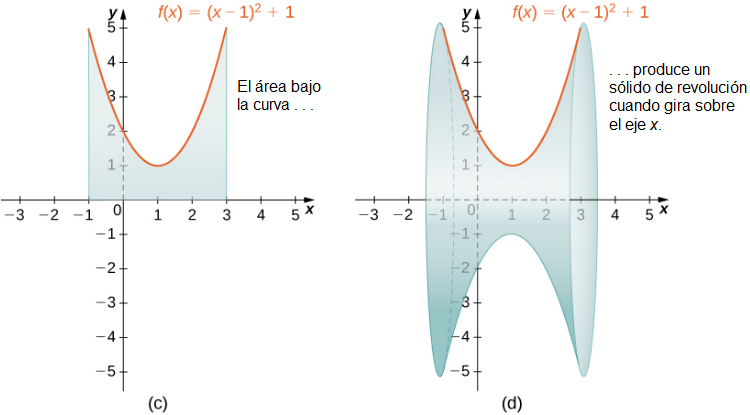
(Figura 6.2_9 (a) Un rectángulo delgado para aproximar el área bajo una curva. (b) Un disco representativo formado al girar el rectángulo alrededor del eje x. (c) La región debajo de la curva gira sobre el eje x, dando como resultado (d) el sólido de revolución.)

Ya usamos el desarrollo formal de la suma de Riemann de la fórmula del volumen cuando desarrollamos el método de las rebanadas. Sabemos que está dada por

La única diferencia con el método del disco es que conocemos la fórmula para el área de la sección transversal con anticipación; es el área de un círculo. Esto da la siguiente regla.

Regla 6.2.1: EL Método del disco

Sea f (x) una función continua y no negativa. Y sea R la región delimitada arriba por la gráfica de f (x), abajo por el eje x, a la izquierda por la recta x = a, y a la derecha por la recta x = b. De tal modo que, el volumen del sólido de revolución formado al girar R alrededor del eje x viene dado por

\( V = \int_a^b \pi [f(x)]^2 dx. \)

---

El volumen del sólido que hemos estado estudiando (Figura 6.2_9) viene dado por

 

Veamos algunos ejemplos.

EJEMPLO ILUSTRATIVO 6.2_3. Uso del método del disco para encontrar el volumen de un sólido de revolución_1

Utilice el método del disco para encontrar el volumen del sólido de revolución generado al rotar la región entre la gráfica de f (x) = √x y el eje x sobre el intervalo [1, 4] alrededor del eje x.

Solución:
Los gráficos de la función y el sólido de revolución se muestran en la siguiente figura.

(Figura 6.2_10 (a) La función f (x) = √x sobre el intervalo [1, 4]. (b) El sólido de revolución obtenido al hacer girar la región debajo de la gráfica de f (x) alrededor del eje x .)

Nosotros tenemos que

El volumen es 15π/2 unidades³. ♦

Ejercicio de control 6.2_3

Utilice el método del disco para encontrar el volumen del sólido de revolución generado al rotar la región entre la gráfica de f (x) = √(4 − x) y el eje x sobre el intervalo [0, 4] alrededor del eje x. ♦

Hasta ahora, nuestros ejemplos tienen todas las regiones interesadas giradas alrededor del eje x, pero podemos generar un sólido de revolución girando una región plana alrededor de cualquier recta horizontal o vertical. En el siguiente ejemplo, observamos un sólido de revolución que se ha generado al girar una región alrededor del eje y. La mecánica del método del disco es casi la misma que cuando el eje x es el eje de revolución, pero expresamos la función en términos de y, además integramos también con respecto a la variable y. Esto se resume en la siguiente regla.

Regla 6.2.2: El método del disco para sólidos de revolución alrededor del eje y

Sea  g (y) una función continua y no negativa. Y sea  Q la región delimitada a la derecha por la gráfica de g (y), a la izquierda por el eje y, debajo por la recta y = c, y arriba por la recta y = d. Entonces, el volumen del sólido de revolución formado al girar Q alrededor del eje y viene dado por

\( V = \int_c^d \pi [g(y)]^2 dy. \)

---

El siguiente ejemplo muestra cómo funciona esta regla en la práctica.

 

EJEMPLO ILUSTRATIVO 6.2_4. Usando el método del disco para encontrar el volumen de un sólido de Revolución_2

Sea R la región delimitada por la gráfica de g(y) = √(4 − y) y el eje y sobre el intervalo del eje y [0, 4]. Utilice el método del disco para encontrar el volumen del sólido de revolución generado al girar R alrededor del eje y.

Solución:

La figura 6.2_11 muestra la función y un disco representativo que se puede usar para estimar el volumen. Observe que, dado que estamos haciendo girar la función alrededor del eje y, los discos son horizontales, en lugar de verticales.

(Figura 6.2_11 (a) Se muestra un rectángulo delgado entre la curva de la función g(y) = √(4 − y) y el eje y. (b) El rectángulo forma un disco representativo después de la revolución alrededor del eje y.)

La región a girar y el sólido completo de la revolución se muestran en la siguiente figura.

(Figura 6.2_12 (a) La región a la izquierda de la función g(y) = √(4 − y) sobre el intervalo del eje y [0, 4]. (b) El sólido de revolución formado al hacer girar la región sobre el eje y.)

Para encontrar el volumen, integramos con respecto a y. Obtenemos

El volumen es de 8π unidades³. ♦

Ejercicio de control 6.2_4

Utilice el método del disco para encontrar el volumen del sólido de revolución generado al rotar la región entre la gráfica de g(y) = y y el eje y sobre el intervalo [1, 4] alrededor del eje y. ♦

El método de las arandelas

Algunos sólidos de revolución tienen cavidades en el medio; no son sólidos hasta el eje de revolución. A veces, esto es solo el resultado de la manera en que se forma la región de revolución con respecto al eje de revolución. En otros casos, las cavidades surgen cuando la región de revolución se define como la región entre las gráficas de dos funciones. Una tercera forma en que esto puede suceder es cuando se selecciona un eje de revolución que no sea el eje x o el eje y.

Cuando el sólido de revolución tiene una cavidad en el medio, las rodajas utilizadas para aproximar el volumen no son discos, sino arandelas (discos con agujeros en el centro). Por ejemplo, considere la región limitada por la gráfica de la función f (x) = √x y por debajo por la gráfica de la función g(x) = 1 en el intervalo [1, 4]. Cuando esta región gira alrededor del eje x, el resultado es un sólido con una cavidad en el medio, y las rodajas son arandelas. El gráfico de la función y una arandela representativa se muestran en la Figura 6.8 (a) y (b). La región de revolución y el sólido resultante se muestran en la Figura 6.2.13 (c) y (d).

(Figura 6.2_13 (a) Un rectángulo delgado en la región entre dos curvas. (b) Un disco representativo formado al girar el rectángulo alrededor del eje x. (c) La región entre las curvas sobre el intervalo dado. (d) El sólido resultante de la revolución).

El área de la sección transversal, entonces, es el área del círculo exterior menos el área del círculo interior. En este caso,

A(x) = π(√x)² − π(1)² = π(x − 1).

Entonces el volumen del sólido es

La generalización de este proceso se conoce como el método de las arandelas.

Regla 6.2.3: El método de las arandelas

Suponga que f (x) y g(x) son funciones continuas, no negativas, y de modo que f (x) ≥ g (x) sobre el intervalo cerrado [a, b]. Supongamos además que R denota la región limitada por la gráfica de f (x), debajo por la gráfica de g(x), a la izquierda por la recta x = a, y a la derecha por la recta x = b. Entonces, el volumen del sólido de revolución formado al girar R alrededor del eje x viene dado por

\( V = \int_a^b \pi [(f(x))^2 – (g(x))^2] dx. \)

---

EJEMPLO ILUSTRATIVO 6.2_5. Usando el método de las arandelas

Encuentre el volumen de un sólido de revolución formado al girar la región delimitada arriba por la gráfica de f (x) = x y abajo por la gráfica de g(x) = 1/x sobre el intervalo [1, 4] alrededor del eje x.

Solución:
Las gráficas de las funciones y el sólido de revolución se muestran en la siguiente figura.

(Figura 9.2_14 (a) La región entre las gráficas de las funciones f (x) = x y g(x) = 1/x en el intervalo [1, 4]. (b) Revolución de la región alrededor del eje x genera un sólido de revolución con una cavidad en el medio).

Tenemos que

♦

Ejercicio de control 6.2_5

Encuentre el volumen de un sólido de revolución formado al girar la región limitada por las gráficas de f (x) = √x y g(x) = 1/x en el intervalo [1, 3] alrededor del eje x. ♦

Al igual que con el método de disco, también podemos aplicar el método de las arandelas a los sólidos de revolución que resultan de girar una región alrededor del eje y. En este caso, se aplica la siguiente regla.

Regla 6.2.4: El método de las arandelas para sólidos de revolución alrededor del eje y

Suponga que u(y) y v(y) son funciones continuas, no negativas, de modo que v(y) ≤ u(y) para y ∈ [c, d]. Supongamos que Q denota la región limitada a la derecha por la gráfica de u(y), a la izquierda por la gráfica de v(y), debajo por la recta y = c, y arriba por la recta y = d. Entonces, el volumen del sólido de revolución formado al girar Q alrededor del eje y viene dado por

\( V = \int_c^d \pi [(u(y))^2 – (v(y))^2] dy. \)

       En lugar de mirar un ejemplo del método de arandela con el eje y como eje de revolución, ahora consideramos un ejemplo en el que el eje de revolución es una línea distinta de uno de los dos ejes de coordenadas. Se aplica el mismo método general, pero es posible que tenga que visualizar cómo describir el área de la sección transversal del volumen.

EJEMPLO ILUSTRATIVO 6.2_6. El método de arandelas con un eje de revolución diferente

Encuentre el volumen de un sólido de revolución formado al girar la región limitada arriba por f (x) = 4 − x y abajo por el eje x sobre el intervalo [0, 4] alrededor de la línea y = −2.

Solución:
La gráfica de la región y el sólido de revolución se muestran en la siguiente figura.

(Figura 6.2_15 (a) La región entre la gráfica de la función f (x) = 4 − x y el eje x sobre el intervalo [0, 4]. (b) Revolución de la región alrededor de la línea y = −2 genera un sólido de revolución con un agujero cilíndrico en el medio).

No podemos aplicar la fórmula del volumen a este problema directamente porque el eje de revolución no es uno de los ejes de coordenadas. Sin embargo, todavía sabemos que el área de la sección transversal es el área del círculo exterior menos el área del círculo interior. Mirando la gráfica de la función, vemos que el radio del círculo exterior está dado por f (x) + 2, que se simplifica a

f (x) + 2 = (4 − x) + 2 = 6 − x.

El radio del círculo interior es g(x) = 2. Por lo tanto, tenemos que

♦

Ejercicio de control 6.2_6

Encuentre el volumen de un sólido de revolución formado al girar la región limitada arriba por la gráfica de f (x) = x + 2 y abajo por el eje x sobre el intervalo [0, 3] alrededor de la línea y = −1. ♦