| 9. Ecuaciones diferenciales | 9.7. Soluciones en serie de ecuaciones lineales de segundo orden | 9.7.2 Soluciones en serie cerca de un punto ordinario I |
Ejercicios propuestos del Capítulo 9.7.2
En los ejercicios 1 a 8, encuentre la serie de potencias en x para la solución general.
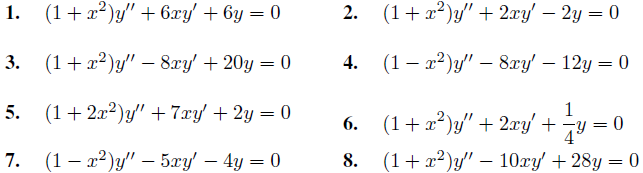
9. (L) (a) Halle la serie de potencias en \(x\) para la solución general de
\[
y^{\prime\prime} + x\,y^{\prime} + 2y = 0.
\]
(b) Para varias elecciones de \(a_0\) y \(a_1\), use software de ecuaciones diferenciales para resolver numéricamente el problema de valor inicial
\[
y^{\prime\prime} + x\,y^{\prime} + 2y = 0,\qquad y(0)=a_0,\qquad y^{\prime}(0)=a_1,
\]
numéricamente en \((-5,5)\).
(c) Para \(r\) fijo en \(\{1,2,3,4,5\}\) gráfico
\[
T_N(x)=\sum_{n=0}^{N} a_n x^n
\]
y la solución obtenida en (a) en \((-r,r)\). Continúe aumentando \(N\) hasta que no haya una diferencia perceptible entre las dos gráficas.
10. (L) Siga las indicaciones del Ejercicio 9 para la ecuación diferencial
\[
y^{\prime\prime} + 2x\,y^{\prime} + 3y = 0.
\]
En los Ejercicios 11–13 encuentre \(a_0, \ldots , a_N\) para \(N \ge 7\) en la solución en serie de potencias
\[
y = \sum_{n=0}^{\infty} a_n x^n
\]
del problema de valor inicial.
11. C \((1 + x^2)y^{\prime\prime} + x y^{\prime} + y = 0,\quad y(0)=2,\quad y^{\prime}(0)=-1.\)
12. C \((1 + 2x^2)y^{\prime\prime} – 9x y^{\prime} – 6y = 0,\quad y(0)=1,\quad y^{\prime}(0)=-1.\)
13. C \((1 + 8x^2)y^{\prime\prime} + 2y = 0,\quad y(0)=2,\quad y^{\prime}(0)=-1.\)
14. L Haga el siguiente experimento para varias elecciones de números reales \(a_0,\; a_1\) y \(r\), con \(0< r < 1/\sqrt{2}\).
(a) Use software de ecuaciones diferenciales para resolver el problema de valor inicial
\[
(1 – 2x^2)\,y^{\prime\prime} – x\,y^{\prime} + 3y = 0,\qquad y(0)=a_0,\qquad y^{\prime}(0)=a_1, \tag{A}
\]
numéricamente en \((-r,r)\).
(b) Para \(N = 2,3,4,\dots\) calcule \(a_2,\dots,a_N\) en la solución en serie de potencias \(y=\sum_{n=0}^{\infty} a_n x^n\) del problema (A), y grafique
\[
T_N(x)=\sum_{n=0}^{N} a_n x^n
\]
y la solución obtenida en (a) en \((-r,r)\). Continúe aumentando \(N\) hasta que no haya una diferencia perceptible entre las dos gráficas.
15. [L] Haga (a) y (b) para varios valores de $r$ en $(0, 1)$:
(a) Use software de ecuaciones diferenciales para resolver el problema de valor inicial
\[ (1+x^2)y^{\prime\prime} + 10xy’ + 14y = 0, \quad y(0) = 5, \quad y'(0) = 1, \quad \text{(A)} \]
numéricamente en $(-r, r)$.
(b) Para $N = 2, 3, 4, \dots$, calcule $a_2, \dots, a_N$ en la solución por series de potencias $y = \sum_{n=0}^{\infty} a_n x^n$ de (A), y grafique
\[ T_N(x) = \sum_{n=0}^{N} a_n x^n \]
y la solución obtenida en (a) en $(-r, r)$. Continúe aumentando $N$ hasta que no haya diferencia perceptible entre las dos gráficas. ¿Qué sucede con el $N$ requerido a medida que $r \to 1$?
(c) Intente (a) y (b) con $r = 1.2$. Explique sus resultados.
En los ejercicios 16 a 20, encuentre la serie de potencias en x − x0 para la solución general.
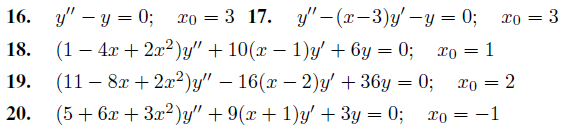
En los Ejercicios 21 – 26 halle $a_0, \dots, a_N$ para $N$ por lo menos $7$ en la serie de potencias $y = \sum_{n=0}^{\infty} a_n (x-x_0)^n$ para la solución del problema de valor inicial. Tome $x_0$ como el punto donde se imponen las condiciones iniciales.
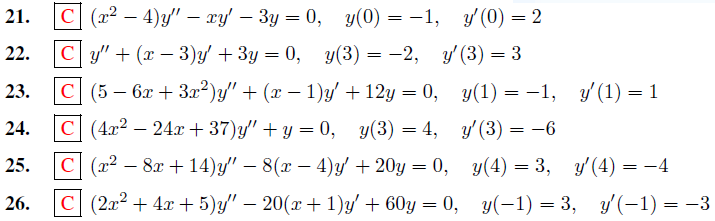
27. (a) Halle una serie de potencias en $x$ para la solución general de
\[ (1+x^2)y” + 4xy’ + 2y = 0. \quad \text{(A)} \]
(b) Use (a) y la fórmula
\[ \frac{1}{1-r} = 1 + r + r^2 + \dots + r^n + \dots \quad (-1 < r < 1) \]
para la suma de una serie geométrica para hallar una expresión en forma cerrada para la solución general de (A) en $(-1, 1)$.
(c) Muestre que la expresión obtenida en (b) es en realidad la solución general de (A) en $(-\infty, \infty)$.
28. Use el Teorema 9.7.2.2 para mostrar que la serie de potencias en $x$ para la solución general de
\[ (1 + \alpha x^2)y^{\prime\prime} + \beta x y’ + \gamma y = 0 \]
es
\[ y = a_0 \sum_{m=0}^{\infty} (-1)^m \left[\prod_{j=0}^{m-1} p(2j)\right] \frac{x^{2m}}{(2m)!} + a_1 \sum_{m=0}^{\infty} (-1)^m \left[\prod_{j=0}^{m-1} p(2j+1)\right] \frac{x^{2m+1}}{(2m+1)!}. \]
29. Use el Ejercicio 28 para mostrar que todas las soluciones de
\[ (1 + \alpha x^2)y^{\prime\prime} + \beta x y’ + \gamma y = 0 \]
son polinomios si y solo si
\[ \alpha n(n-1) + \beta n + \gamma = \alpha(n – 2r)(n – 2s – 1), \]
donde $r$ y $s$ son enteros no negativos.
30. (a) Use el Ejercicio 28 para mostrar que la serie de potencias en $x$ para la solución general de
\[ (1 – x^2)y^{\prime\prime} – 2bxy’ + \alpha(\alpha + 2b – 1)y = 0 \]
es $y = a_0 y_1 + a_1 y_2$, donde
\[ y_1 = \sum_{m=0}^{\infty} \left[\prod_{j=0}^{m-1} (2j – \alpha)(2j + \alpha + 2b – 1)\right] \frac{x^{2m}}{(2m)!} \]
y
\[ y_2 = \sum_{m=0}^{\infty} \left[\prod_{j=0}^{m-1} (2j + 1 – \alpha)(2j + \alpha + 2b)\right] \frac{x^{2m+1}}{(2m + 1)!}. \]
(b) Suponga que $2b$ no es un entero impar negativo y $k$ es un entero no negativo. Muestre que $y_1$ es un polinomio de grado $2k$ tal que $y_1(-x) = y_1(x)$ si $\alpha = 2k$, mientras que $y_2$ es un polinomio de grado $2k+1$ tal que $y_2(-x) = -y_2(x)$ si $\alpha = 2k+1$. Concluya que si $n$ es un entero no negativo, entonces hay un polinomio $P_n$ de grado $n$ tal que $P_n(-x) = (-1)^n P_n(x)$ y
\[ (1 – x^2)P_n^{\prime\prime} – 2bxP_n’ + n(n+2b-1)P_n = 0. \quad \text{(A)} \]
(c) Muestre que (A) implica que
\[ [(1-x^2)^b P_n’]’ = -n(n+2b-1)(1-x^2)^{b-1}P_n, \]
y use esto para mostrar que si $m$ y $n$ son enteros no negativos, entonces
\[ [(1-x^2)^b P_m’]’ P_n – [(1-x^2)^b P_n’]’ P_m = [m(m+2b-1) – n(n+2b-1)](1-x^2)^b P_m P_n. \quad \text{(B)} \]
(d) Ahora suponga $b > 0$. Use (B) y la integración por partes para mostrar que si $m \ne n$, entonces
\[ \int_{-1}^{1} (1-x^2)^{b-1} P_m(x) P_n(x) \, dx = 0. \]
(Decimos que $P_m$ y $P_n$ son ortogonales en $(-1, 1)$ con respecto a la función de peso $(1-x^2)^{b-1}$.)
31. (a) Use el Ejercicio 28 para mostrar que la serie de potencias en $x$ para la solución general de la ecuación de Hermite
\[ y^{\prime\prime} – 2xy’ + 2\alpha y = 0 \]
es $y = a_0 y_1 + a_1 y_2$, donde
\[ y_1 = \sum_{m=0}^{\infty} \left[\prod_{j=0}^{m-1} (2j – \alpha)\right] \frac{2^m x^{2m}}{(2m)!} \]
y
\[ y_2 = \sum_{m=0}^{\infty} \left[\prod_{j=0}^{m-1} (2j + 1 – \alpha)\right] \frac{2^m x^{2m+1}}{(2m + 1)!}. \]
(b) Suponga que $k$ es un entero no negativo. Muestre que $y_1$ es un polinomio de grado $2k$ tal que $y_1(-x) = y_1(x)$ si $\alpha = 2k$, mientras que $y_2$ es un polinomio de grado $2k+1$ tal que $y_2(-x) = -y_2(x)$ si $\alpha = 2k+1$. Concluya que si $n$ es un entero no negativo, entonces hay un polinomio $P_n$ de grado $n$ tal que $P_n(-x) = (-1)^n P_n(x)$ y
\[ P_n^{\prime\prime} – 2xP_n’ + 2nP_n = 0. \quad \text{(A)} \]
(c) Muestre que (A) implica que
\[ [e^{-x^2} P_n’]’ = -2ne^{-x^2} P_n, \]
y use esto para mostrar que si $m$ y $n$ son enteros no negativos, entonces
\[ [e^{-x^2} P_m’]’ P_n – [e^{-x^2} P_n’]’ P_m = 2(m-n)e^{-x^2} P_m P_n. \quad \text{(B)} \]
(d) Use (B) y la integración por partes para mostrar que si $m \ne n$, entonces
\[ \int_{-\infty}^{\infty} e^{-x^2} P_m(x) P_n(x) \, dx = 0. \]
(Decimos que $P_m$ y $P_n$ son ortogonales en $(-\infty, \infty)$ con respecto a la función de peso $e^{-x^2}$.)
32. Considere la ecuación
\[ (1 + \alpha x^3)y^{\prime\prime} + \beta x^2 y’ + \gamma y = 0, \quad \text{(A)} \]
y sea $p(n) = \alpha n(n-1) + \beta n + \gamma$. (El caso especial $y” – xy = 0$ de (A) es la ecuación de Airy.)
(a) Modifique el argumento usado para demostrar el Teorema 9.7.2.2. para mostrar que
\[ y = \sum_{n=0}^{\infty} a_n x^n \]
es una solución de (A) si y solo si $a_2 = 0$ y
\[ a_{n+3} = -\frac{p(n)}{(n+3)(n+2)} a_n, \quad n \ge 0. \]
(b) Muestre a partir de (a) que $a_n = 0$ a menos que $n = 3m$ o $n = 3m + 1$ para algún entero no negativo $m$, y que
\[ a_{3m+3} = -\frac{p(3m)}{(3m+3)(3m+2)} a_{3m}, \quad m \ge 0, \]
y
\[ a_{3m+4} = -\frac{p(3m+1)}{(3m+4)(3m+3)} a_{3m+1}, \quad m \ge 0, \]
donde $a_0$ y $a_1$ pueden especificarse arbitrariamente.
(c) Concluya a partir de (b) que la serie de potencias en $x$ para la solución general de (A) es
\[ y = a_0 \sum_{m=0}^{\infty} (-1)^m \left[ \prod_{j=0}^{m-1} \frac{p(3j)}{3j+2} \right] \frac{x^{3m}}{3^m m!} + a_1 \sum_{m=0}^{\infty} (-1)^m \left[ \prod_{j=0}^{m-1} \frac{p(3j+1)}{3j+4} \right] \frac{x^{3m+1}}{3^m m!}. \]
En los Ejercicios 33 a 37 utilice el método del Ejercicio 32 para encontrar la serie de potencias en x para la solución general.
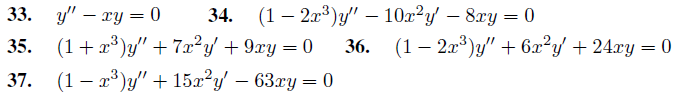
38. Considere la ecuación
\[ (1 + \alpha x^{k+2})y^{\prime\prime} + \beta x^k y’ + \gamma y = 0, \quad \text{(A)} \]
donde $k$ es un entero positivo, y sea $p(n) = \alpha n(n-1) + \beta n + \gamma$.
(a) Modifique el argumento usado para demostrar el Teorema 9.7.2.2. para mostrar que
\[ y = \sum_{n=0}^{\infty} a_n x^n \]
es una solución de (A) si y solo si $a_n = 0$ para $2 \le n \le k+1$ y
\[ a_{n+k+2} = -\frac{p(n)}{(n+k+2)(n+k+1)} a_n, \quad n \ge 0. \]
(b) Muestre a partir de (a) que $a_n = 0$ a menos que $n = (k+2)m$ o $n = (k+2)m + 1$ para algún entero no negativo $m$, y que
\[ a_{(k+2)(m+1)} = -\frac{p((k+2)m)}{(k+2)(m+1)[(k+2)(m+1)-1]} a_{(k+2)m}, \quad m \ge 0, \]
y
\[ a_{(k+2)m+k+2} = -\frac{p((k+2)m + 1)}{[(k+2)m + k + 2][(k+2)m + k + 1]} a_{(k+2)m+1}, \quad m \ge 0, \]
donde $a_0$ y $a_1$ pueden especificarse arbitrariamente.
(c) Concluya a partir de (b) que la serie de potencias en $x$ para la solución general de (A) es
\[ y = a_0 \sum_{m=0}^{\infty} (-1)^m \left[ \prod_{j=0}^{m-1} \frac{p((k+2)j)}{(k+2)j + 1} \right] \frac{x^{(k+2)m}}{(k+2)^m m!} + a_1 \sum_{m=0}^{\infty} (-1)^m \left[ \prod_{j=0}^{m-1} \frac{p((k+2)j + 1)}{(k+2)j + 2} \right] \frac{x^{(k+2)m+1}}{(k+2)^m m!}. \]
En los Ejercicios 39 a 44, utilice el método del Ejercicio 38 para encontrar la serie de potencias en x para la solución general.
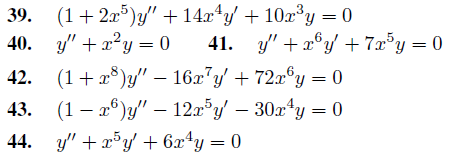
9.7.3: Soluciones en serie cerca de un punto ordinario II »
