| 9. Ecuaciones diferenciales | 9.5 Ecuaciones lineales de segundo orden | 9.5.7 Variación de parámetros |
Ejercicios propuestos para el capítulo 9.5.7
En los ejercicios 1 a 6, use la variación de parámetros para encontrar una solución particular.
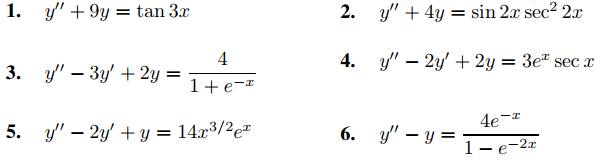
En los Ejercicios 7 a 29 use la variación de parámetros para encontrar una solución particular, dadas las soluciones y1, y2 de la ecuación complementaria.
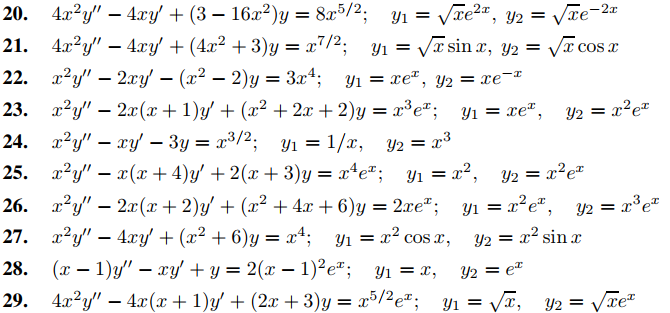
En los ejercicios 30 a 32 utilice la variación de parámetros para resolver el problema de valor inicial, dado que y1, y2 son soluciones de la ecuación complementaria.
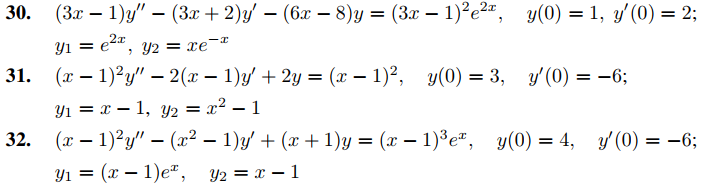
En los Ejercicios 33 a 35 utilice la variación de parámetros para resolver el problema de valor inicial y grafique la solución, dado que y1, y2 son soluciones de la ecuación complementaria.
36. Supongamos que
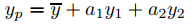
es una solución particular de
P0(x)y′′ + P1(x)y′ + P2(x)y = F(x), (A)
donde y1 e y2 son soluciones de la ecuación complementaria
P0(x)y′′ + P1(x)y′ + P2(x)y = 0
Demuestre que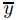 
es también una solución de (A).
37. Suponga que p, q y f son continuas en (a, b) y sea x0 en (a, b). Sean y1 e y2 las soluciones de
y′′ + p(x)y′ + q(x)y = 0
tal que
y1(x0) = 1, y1′ (x0) = 0, y2(x0) = 0, y2′ (x0) = 1.
Use la variación de parámetros para mostrar que la solución del problema de valor inicial
y′′ + p(x)y′ + q(x)y = f (x), y(x0) = k0, y′(x0) = k1,
es
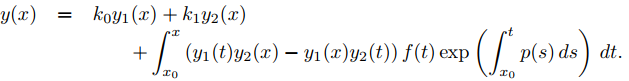
AYUDA: Use la fórmula de Abel para el Wronskiano de {y1, y2} e integre u1′ y u2′ de x0 a x. Muestre también que
38. Suponga que f es continua en un intervalo abierto que contiene x0 = 0. Use la variación de parámetros para encontrar una fórmula para la solución del problema de valor inicial
y′′ − y = f (x), y(0) = k0, y′(0) = k1
39. Suponga que f es continua en (a, ∞), donde a < 0, entonces x0 = 0 está en (a, ∞).
(a) Use la variación de parámetros para encontrar una fórmula para la solución del problema de valor inicial
y′′ + y = f (x), y(0) = k0, y′(0) = k1
SUGERENCIA: necesitará las fórmulas de suma para el seno y el coseno:
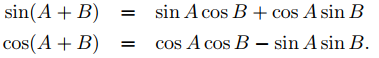
Para el resto de este ejercicio suponga que la integral impropia 
es absolutamente convergente.
(b) Demuestre que si y es una solución de
y′′ + y = f (x) (A)
en (a, ∞), entonces
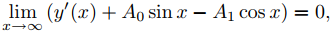(B)
y
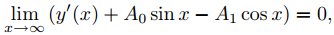(C)
donde
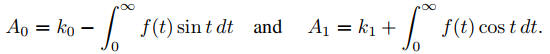
AYUDA: Recuerde del cálculo que si converge absolutamente, entonces 
(c) Demuestre que si A0 y A1 son constantes arbitrarias, entonces hay una única solución de y′′ + y = f (x) en (a, ∞) que satisface (B) y (C).