| 9. Ecuaciones diferenciales | 9.4. Aplicaciones de ecuaciones de primer orden | 9.4.4 Ecuaciones autónomas de segundo orden |
Ejercicios propuestos para el Capítulo 9.4.4
En los ejercicios 1 a 4, encuentre las ecuaciones de las trayectorias de la ecuación no amortiguada dada. Identifique las soluciones de equilibrio, determine si son estables o inestables y trace algunas trayectorias. SUGERENCIA: Use la Ecuación 9.4.4.8 para obtener las ecuaciones de las trayectorias.
En los ejercicios 5 a 8, encuentre las ecuaciones de las trayectorias de la ecuación no amortiguada dada. Identifique las soluciones de equilibrio, determine si son estables o inestables y encuentre las ecuaciones de las separatrices (es decir, las curvas a través de los equilibrios inestables). Trazar las separatrices y algunas trayectorias en cada una de las regiones del plano de Poincaré determinadas por ellas. SUGERENCIA: Use la Ecuación 9.4.4.17 para determinar las separatrices.
En los ejercicios 9 a 12, trace algunas trayectorias de la ecuación dada para varios valores (positivo, negativo, cero) del parámetro a. Encuentra los equilibrios de la ecuación y clasifícalos como estables o inestables. Explique por qué las gráficas del plano de fase correspondientes a valores positivos y negativos de a difieren tan marcadamente. ¿Puedes pensar en una razón por la cual cero merece ser llamado el valor crítico de a?
En los ejercicios 13 a 18, grafique las trayectorias de la ecuación dada para c = 0 y valores pequeños distintos de cero (positivos y negativos) de c para observar los efectos del amortiguamiento.
19. L La ecuación de van der Pol
y′′ − µ(1 − y2)y′ + y = 0, (A)
donde µ es una constante positiva e y es la corriente eléctrica (Sección 9.6.3), surge en el estudio de un circuito eléctrico cuyas propiedades resistivas dependen de la corriente. El término de amortiguamiento −µ(1 − y2)y′ sirve para reducir |y| si |y| < 1 o para aumentar |y| si |y| > 1. Se puede demostrar que la ecuación de van der Pol tiene exactamente una trayectoria cerrada, que se denomina ciclo límite. Las trayectorias dentro del ciclo límite giran en espiral hacia afuera, mientras que las trayectorias fuera del ciclo límite giran en espiral hacia adentro (Figura 9.4.4.16). Use su software de ecuaciones diferenciales favorito para verificar esto para µ = 0.5, 1.1.5,2. Usa una cuadrícula con −4 < y < 4 y −4 < v < 4.
Figura 9.4.4.16 Trayectorias de la ecuación de van der Pol
20. L Ecuación de Rayleigh,
y′′ − µ(1 − (y′)2/3)y′ + y = 0
también tiene un ciclo límite. Siga las instrucciones del Ejercicio 19 para esta ecuación.
21. En relación con la Ecuación 9.4.4.15, suponga que y(0) = 0 y y′(0) = v0, donde 0 < v0 < vc.
(a) Sea T1 el tiempo necesario para que y aumente de cero a ymax = 2 sen−1(v0/vc). Muestre que
(A)
(b) Separe las variables en (A) y demuestre que
(B)
(c) Sustituya senu/2 = (v0/vc) senθ en (B) para obtener
(C)
(d) Concluya a partir de la simetría que el tiempo necesario para que (y(t), v(t)) recorra la trayectoria
v2 = v02 − vc2 sen2y/2
es T = 4T1, y que en consecuencia y(t + T) = y(t) y v(t + T) = v(t); es decir, la oscilación es periódica con período T.
(e) Demuestre que si v0 = vc, la integral en (C) es impropia y diverge hacia ∞. Concluya de esto que y(t) < π para todo t y limt→∞ y(t) = π.
22. Dé una definición directa de un equilibrio inestable de y′′ + p(y) = 0.
23. Sea p continua para todo y y p(0) = 0. Supongamos que existe un número positivo ρ tal que p(y) > 0 si 0 < y ≤ ρ y p(y) < 0 si −ρ ≤ y < 0. Para 0 < r ≤ ρ sea
y 
Sea y la solución del problema de valor inicial
y′′ + p(y) = 0, y(0) = v0, y′(0) = v0,
y definir 
(a) Demuestre que
0 < c(y0, v0) < v02 + 2β(|y0|) si 0 < |y0| ≤ ρ.
(b) Demuestre que
(c) Concluya de (b) que si c(y0, v0) < 2α(r) entonces |y| < r, t > 0.
(d) Dado ε > 0, sea δ > 0 elegido de modo que
Demuestra que si 
entonces 
para t > 0, lo que implica que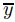 
= 0 es un equilibrio estable de y′′ + p(y) = 0.
(e) Ahora sea p continua para todo y y p(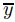) = 0, donde 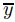no es necesariamente cero. Supongamos que hay un número positivo ρ tal que p(y) > 0 si 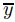< y ≤ 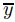+ ρ y p(y) < 0 si 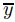− ρ ≤ y < 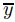. Demuestre que 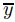es un equilibrio estable de y′′ + p(y) = 0.
24. Sea p continua para todo y.
(a) Suponga que p(0) = 0 y hay un número positivo ρ tal que p(y) < 0 si 0 < y ≤ ρ. Sea cualquier número tal que 0 < ε < ρ. Demostrar que si y es la solución del problema de valor inicial
y′′ + p(y) = 0, y(0) = y0, y′(0) = 0
con 0 < y0 < ε, entonces y(t) ≥ ε para algún t > 0. Concluya que 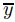= 0 es un equilibrio inestable de y′′ + p(y) = 0.
AYUDA: Sea k = minyo ≤ x ≤ ε (−p(x)), que es positivo. Demuestre que si y(t) < ε para 0 ≤ t < T entonces kT2 < 2(ε − y0).
(b) Ahora sea p(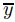) = 0, donde 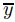no es necesariamente cero. Supongamos que hay un número positivo ρ tal que p(y) < 0 si 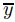< y ≤ 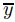+ ρ. Demuestre que 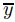es un equilibrio inestable de y′′ + p(y) = 0.
(c) Modifique sus pruebas de (a) y (b) para mostrar que si hay un número positivo ρ tal que p(y) > 0 si 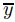− ρ ≤ y < 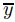, entonces 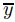es un equilibrio inestable de y′′ + p(y) = 0.