| 9. Ecuaciones diferenciales | 9.12. Soluciones de Fourier de ecuaciones diferenciales parciales | 9.12.2. La ecuación de onda |

Ejercicios propuestos para el Capítulo 9.12.2.2

      En los Ejercicios 1 a 15 resuelva el problema de valor inicial y de frontera. En algunos de estos ejercicios, el Teorema 9.11.3.5(b) o el Ejercicio 9.11.3.35 simplificarán el cálculo de los coeficientes en la serie de senos de Fourier.

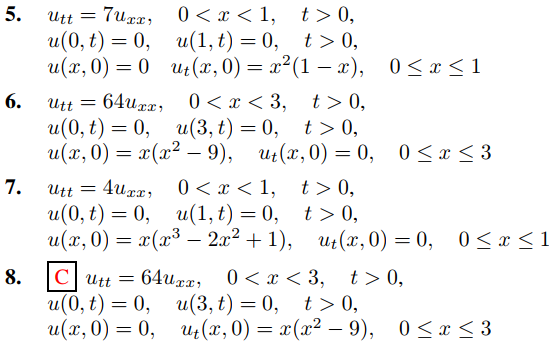
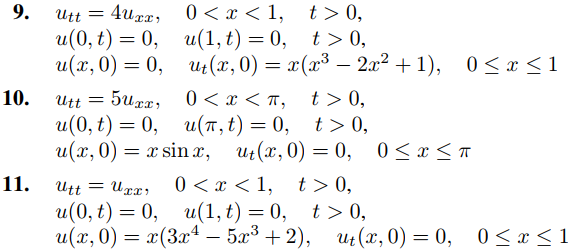
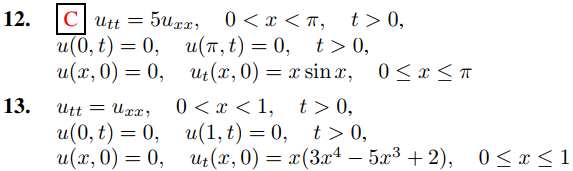
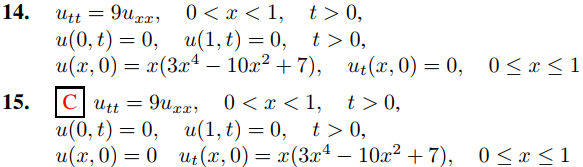
16. Vimos que el desplazamiento de la cuerda pulsada es, por un lado,

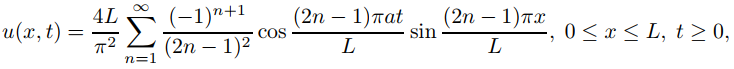       (A)

y, por otro lado,

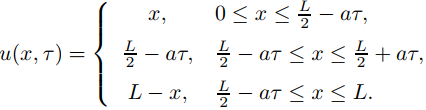       (B)

si 0 ≤ τ ≤ L/2a. El primer objetivo de este ejercicio es mostrar que (B) se puede usar para calcular u(x, t) para 0 ≤ x ≤ L y todo t > 0.

(a) Demuestre que si t > 0, existe un entero no negativo m tal que

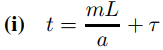       o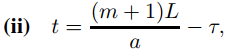     

donde 0 ≤ τ ≤ L/2a.

(b) Use (A) para mostrar que u(x, t) = (−1)^mu(x, τ) si (i) se cumple, mientras que u(x, t) = (−1)^m+1u(x, τ) si (ii) se cumple.

(c) L Realice el siguiente experimento para valores específicos de L y a y varios valores de m y k: Sea

por lo tanto, t₀, t₁, . . . , t_k son puntos igualmente espaciados en [0, L/2a]. Para cada j = 0, 1, 2,. . . , k, grafique la m-ésima suma parcial de (A) y u(x, t_j) calculada a partir de (B) en el mismo eje. Cree una animación, como se describe en los comentarios sobre el uso de la tecnología al final de la sección.

17. Si una cuerda vibra con el extremo en x = 0 libre para moverse en una pista vertical sin fricción y el extremo en x = L fijo, entonces el problema de valor inicial y de frontera para su desplazamiento toma la form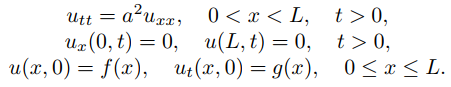a

       (A)

Justifique la definición de la solución formal de (A) como

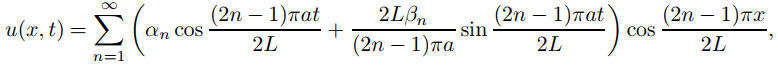
donde

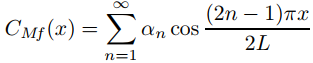   y 

son las series mixtas de cosenos de Fourier de f y g en [0, L]; es decir,

   y 

      En los ejercicios 18 a 31, use el Ejercicio 17 para resolver el problema de valor inicial y de frontera. En algunos de estos ejercicios, el Teorema 9.11.3.5(c) o el Ejercicio Ejercicio 9.11.3.42 (b) simplificarán el cálculo de los coeficientes en la serie mixta de cosenos de Fourier.

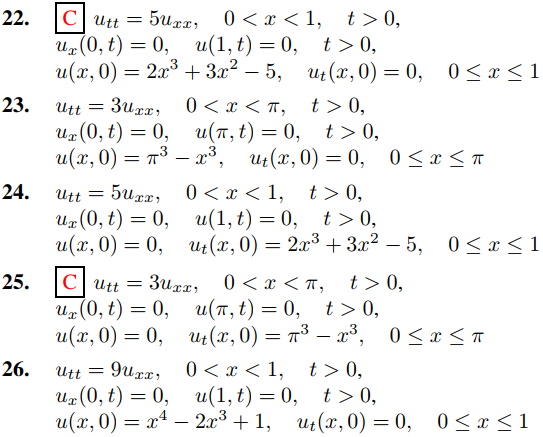
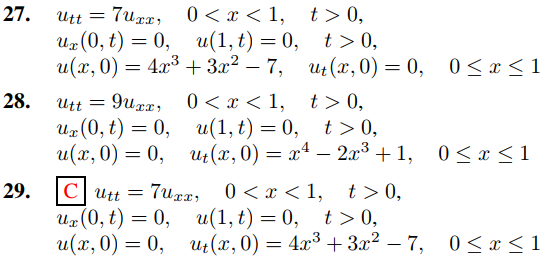
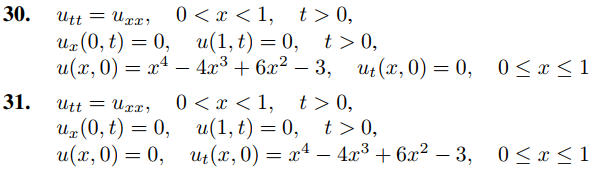
32. Adapte la prueba del Teorema 9.12.2.1 para encontrar la solución de d’Alembert del problema de valor inicial y de frontera del ejercicio 17.

33. Use el resultado del ejercicio 32 para mostrar que la solución formal del problema de valor inicial y de frontera en el ejercicio 17 es una solución real si g es diferenciable y f es dos veces diferenciable en [0, L] y

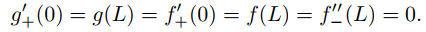
AYUDA: Vea el Ejercicio 9.11.3.57 y aplique el Teorema 9.12.2.2 reemplazando L por 2L.

34. Justificar la definición de la solución formal del problema del valor inicial y de frontera

sea

donde

    y   

son las series mixtas de senos de Fourier de f y g en [0, L]; es decir,

    y   

      En los ejercicios 35 a 46, use el ejercicio 34 para resolver el problema de valor inicial y de frontera. En algunos de estos ejercicios, el Teorema 9.11.3.5(d) o el Ejercicio 9.11.3.50 (b) simplificarán el cálculo de los coeficientes en la serie mixta de senos de Fourier.

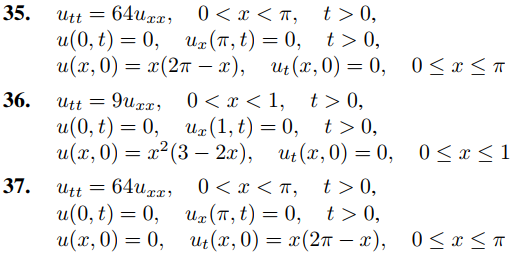
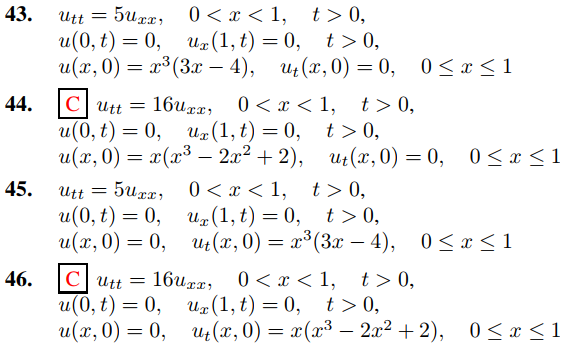
47. Adapte la prueba del Teorema 9.12.2.1 para encontrar la solución de d’Alembert del problema de valor inicial y de frontera del ejercicio 34.

48. Use el resultado del ejercicio 47 para mostrar que la solución formal del problema de valor inicial y de frontera del ejercicio 34 es una solución real si g es diferenciable y f es dos veces diferenciable en [0, L] y

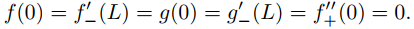
AYUDA: Vea el Ejercicio 9.11.3.58 y aplique el Teorema 9.12.2.2 reemplazando L por 2L.

49. Justifique la definición de la solución formal del problema de valor inicial y de frontera

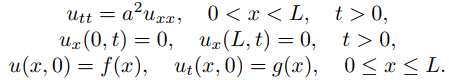
sea

donde

    y   

son las series de cosenos de Fourier de f y g en [0, L]; es decir,

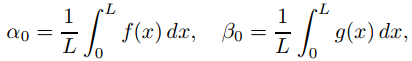     y   

      En los ejercicios 50 a 59, use el ejercicio 49 para resolver el problema de valor inicial y de frontera. En algunos de estos ejercicios, el Teorema 9.11.3.5(a) simplificará el cálculo de los coeficientes en la serie de cosenos de Fourier.

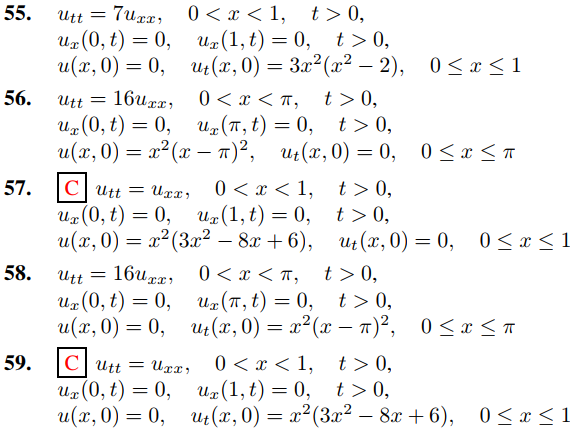
60. Adapte la prueba del Teorema 9.12.2.1 para encontrar la solución de d’Alembert del problema de valor inicial y de frontera inicial del ejercicio 49.

61. Use el resultado del ejercicio 60 para mostrar que la solución formal del problema de valor inicial y de frontera del ejercicio 49 es una solución real si g es diferenciable y f es dos veces diferenciable en [0, L] y

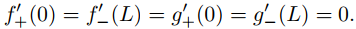
62. Suponga que λ y µ son constantes y p_n(x) = cosnλx  o  p_n(x) = sennλx, mientras que q_n(t) = cosnµt  o  q_n(t) = sennµt para n = 1, 2, 3 , . . .  . Sea

        (A)

donde son constantes.

(a) Demuestre que si converge entonces u(x, t) converge para todo (x, t).

(b) Utilice el Teorema 9.12.1.1 para demostrar que si 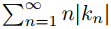converge entonces (A) se puede derivar término a término con respecto a x y t para todo (x, t); es decir,

y

(c) Supongamos que converge. Muestre que

y

(d) Supongamos que y ambos convergen. Demuestre que la solución formal

de la Ecuación 9.12.2.1 satisface u_tt = a²u_xx para todo (x, t).

Esta conclusión también se aplica a las soluciones formales definidas en los ejercicios 17, 34 y 49.

63. Suponga que g es diferenciable y f es dos veces diferenciable en (−∞, ∞), y sea

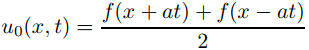    y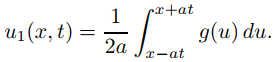   

(a) Demuestre que

y

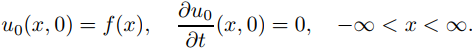(b) Demuestre que

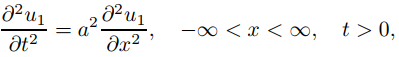
y

(c) Resuelva

      En los Ejercicios 64 a 68 use el resultado del Ejercicio 63 para encontrar una solución de

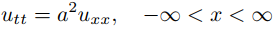
que satisface las condiciones iniciales dadas.