| 9. Ecuaciones diferenciales | 9.1. Introducción a las ecuaciones diferenciales | Ejercicios propuestos para Capítulo 9.1.2 |

9.1.2. CONCEPTOS BÁSICOS

Una ecuación diferencial es una ecuación que contiene una o más derivadas de una función desconocida. El orden de una ecuación diferencial es el orden de la derivada más alta que contiene.

       Una ecuación diferencial es una ecuación diferencial ordinaria si involucra una función desconocida de una sola variable independiente, o una ecuación diferencial parcial si involucra derivadas parciales de una función de más de una variable independiente. Por ahora consideraremos sólo ecuaciones diferenciales ordinarias, y las llamaremos simplemente ecuaciones diferenciales.

A lo largo de este capítulo, todas las variables y constantes son reales a menos que se indique lo contrario. Usualmente usaremos x para la variable independiente a menos que la variable independiente sea el tiempo; entonces usaremos t.
Las ecuaciones diferenciales más simples son ecuaciones de primer orden de la formadonde f es una función conocida de x. Ya sabemos por cálculo cómo encontrar funciones que satisfagan este tipo de ecuaciones. Por ejemplo, si

y′ = x³,

entonces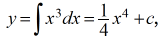donde c es una constante arbitraria. Si n > 1 podemos encontrar funciones y que satisfacen ecuaciones de la formapor integración repetida. Nuevamente, este es un problema de cálculo integral.

Excepto para fines ilustrativos en esta sección, no es necesario considerar ecuaciones diferenciales como (9.1.2_1). Por lo general, consideraremos ecuaciones diferenciales que se pueden escribir como

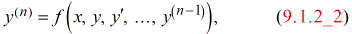
donde al menos una de las funcionesefectivamente aparece a la derecha. Aquí hay unos ejemplos:

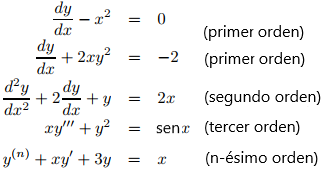
Aunque ninguna de estas ecuaciones está escrita como en (9.1.2_2), todas pueden escribirse de esta forma:

Soluciones de ecuaciones diferenciales

Una solución de una ecuación diferencial es una función que satisface la ecuación diferencial en algún intervalo abierto; así, y es una solución de (9.1.2_2) si y es n veces diferenciable y

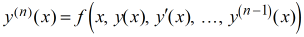
para todas las x en algún intervalo abierto (a, b). En este caso, también decimos que y es una solución de (9.1.2_2) en (a, b).
Las funciones que satisfacen una ecuación diferencial en puntos aislados no son interesantes. Por ejemplo, y = x² satisface

xy′ + x² = 3x

si y sólo si x = 0 o x = 1, pero no es una solución de esta ecuación diferencial porque no satisface la ecuación en un intervalo abierto.

    La gráfica de una solución de una ecuación diferencial es una curva de solución. En términos más generales, se dice que una curva C es una curva integral de una ecuación diferencial si cada función y = y(x) cuya gráfica es un segmento de C es una solución de la ecuación diferencial. Por lo tanto, cualquier curva de solución de una ecuación diferencial es una curva integral, pero una curva integral no necesita ser una curva de solución.

Ejemplo ilustrativo 9.1.2_1

Si a es una constante positiva, la circunferencia

x² + y² = a²         (9.1.2_3)

es una curva integral de

Para ver esto, tenga en cuenta que las únicas funciones cuyas gráficas son segmentos de (9.1.2_3) son

Le dejamos que verifique que estas funciones satisfacen (9.1.2_4) en el intervalo abierto (−a, a) (Ver la verificación dada por ChtatGPT). Sin embargo, (9.1.2_3) no es una curva de solución de (9.1.2_4), ya que no es la gráfica de una función.    ♦

Ejemplo ilustrativo 9.1.2_2

Verifique que

es una solución de

xy′ + y = x²        (9.1.2_6)

en (0, ∞) y en (−∞, 0).

Solución:

Sustituyendo (9.1.2_5) y

en (9.1.2_6), obtenemos

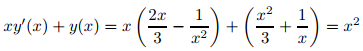
para todo x ≠ 0. Por lo tanto, y es una solución de (9.1.2_6) en (−∞, 0) y (0, ∞). Sin embargo, y no es una solución de la ecuación diferencial en cualquier intervalo abierto que contenga x = 0, ya que y no está definido en x = 0.

    La figura 9.1.2_1 muestra la gráfica de (9.1.2_5). La parte de la gráfica de (9.1.2_5) en (0, ∞) es una curva de solución de (9.1.2_6), al igual que la parte de la gráfica en (−∞, 0).    ♦

Figura 9.1.2_1

Ejemplo ilustrativo 9.1.2_3

Demuestre que si c₁ y c₂ son constantes, entonces

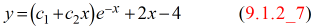
es una solución de 

y″ + 2y′ + y = 2x          (9.1.2_8)

en (−∞, ∞).

Solución:

Diferenciando (9.1.2_7) dos veces, se obtiene

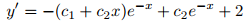
y

entonces

para todos los valores de x. Por lo tanto, y es una solución de (9.1.2_8) en (−∞, ∞).    ♦

Ejemplo ilustrativo 9.1.2_4

Encuentra todas las soluciones de

Solución:

Integrando (9.1.2_9), obtenemos

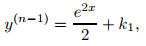
donde k₁ es una constante. Si n = 2, la integración de nuevo produce

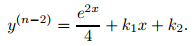
Si n ≥ 3, se obtiene por integración repetida

donde k₁, k₂,. . . , kₙ son constantes. Esto muestra que cada solución de (9.1.2_9) tiene la forma (9.1.2_10) para alguna elección de las constantes k₁, k₂,. . . , kₙ. Por otro lado, diferenciar (9.1.2_10) n veces muestra que si k₁, k₂,. . . , kₙ son constantes arbitrarias, entonces la función y en (9.1.2_10) satisface (9.1.2_9).

Las constantes k₁, k₂,. . . , kₙ en (9.1.2_10) son arbitrarias, al igual que las constantes

Por lo tanto, este ejemplo muestra que todas las soluciones de (9.1.2_9) se pueden escribir como

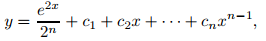
donde cambiamos el nombre de las constantes arbitrarias en (9.1.2_10) para obtener una fórmula más simple. Como regla general, las constantes arbitrarias que aparecen en soluciones de ecuaciones diferenciales deben simplificarse si es posible. Verá ejemplos de esto en todo el capítulo.    ♦

Problemas de valor inicial

En el Ejemplo 9,1,2,4 vimos que la ecuación diferencial

tiene una familia infinita de soluciones que dependen de las n constantes arbitrarias c₁, c₂,. . . cₙ. En ausencia de condiciones adicionales, no hay razón para preferir una solución de una ecuación diferencial sobre otra. Sin embargo, a menudo nos interesará encontrar una solución de una ecuación diferencial que satisfaga una o más condiciones específicas. El siguiente ejemplo ilustra esto.

Ejemplo ilustrativo 9.1.2_5

Encuentre una solución de

y′ = x³

tal que y(1) = 2.

Solución:

Al comienzo de esta sección vimos que las soluciones de y′ = x³ son

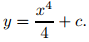
Para determinar un valor de c tal que y(1) = 2, establecemos x = 1 e y = 2 aquí para obtener

2 = y(1) = 1/4 + c, entonces c = 7/4.

Por lo tanto, la solución requerida es

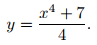
La figura 9.1.2_2 muestra la gráfica de esta solución. Tenga en cuenta que imponer la condición y(1) = 2 es equivalente a requerir que la gráfica de y pase por el punto (1, 2).    ♦

Figura 9.1.2_2

Podemos reescribir el problema considerado en el ejemplo 9.1.2_5 más brevemente como

y′ = x³,    y(1) = 2.

Llamamos a esto un problema de valor inicial. El requisito y(1) = 2 es una condición inicial. También se pueden plantear problemas de valor inicial para ecuaciones diferenciales de orden superior. Por ejemplo,

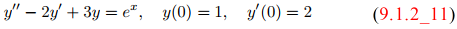
es un problema de valor inicial para una ecuación diferencial de segundo orden donde se requiere que y e y′ tengan valores especificados en x = 0. En general, un problema de valor inicial para una ecuación diferencial de orden n requiere que y y sus primeras n − 1 derivadas tengan valores especificados en algún punto x₀. Estos requisitos son las condiciones iniciales.

       Denotaremos un problema de valor inicial para una ecuación diferencial escribiendo las condiciones iniciales después de la ecuación, como en (9.1.2_11). Por ejemplo, escribiríamos un problema de valor inicial para (9.1.2_2) como

De acuerdo con nuestra definición anterior de una solución de la ecuación diferencial en (9.1.2_12), decimos que y es una solución del problema del valor inicial (9.1.2_12) si y es n veces diferenciable y

para todo x en algún intervalo abierto (a, b) que contiene x₀,  y cumple las condiciones iniciales dadas en (9.1.2_12). El intervalo abierto más grande que contiene x₀ en el que se define y satisface la ecuación diferencial es el intervalo de validez de y.

Ejemplo ilustrativo 9.1.2_6

En el ejemplo 9.1.2_5 vimos que

es una solución del problema de valor inicial

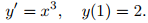
Como la función en (9.1.2_13) está definida para todas las x, el intervalo de validez de esta solución es (−∞, ∞).    ♦

Ejemplo ilustrativo 9.1.2_7

En el ejemplo 9.1.2_2 verificamos que

es una solución de

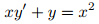
en (0, ∞) y en (−∞, 0). Al evaluar (9.1.2_14) en x = ± 1, puede ver que (9.1.2_14) es una solución de los problemas de valores iniciales

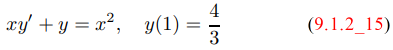
y

El intervalo de validez de (9.1.2_14) como solución de (9.1.2_15) es (0, ∞), ya que este es el intervalo más grande que contiene x₀ = 1 en el que se define (9.1.2_14). Del mismo modo, el intervalo de validez de (9.1.2_14) como solución de (9.1.2_16) es (−∞, 0), ya que este es el intervalo más grande que contiene x₀ = −1 en el que se define (9.1.2_14).    ♦

Caída libre bajo gravedad constante

El término problema de valor inicial se originó en problemas de movimiento donde la variable independiente es t (que representa el tiempo transcurrido), y las condiciones iniciales son la posición y la velocidad de un objeto en el momento inicial (inicio) de un experimento.

Ejemplo ilustrativo 9.1.2_8

Un objeto cae bajo la influencia de la gravedad cerca de la superficie de la Tierra, donde se puede suponer que la magnitud de la aceleración debida a la gravedad es una constante g.

(a) Construya un modelo matemático para el movimiento del objeto en forma de un problema de valor inicial para una ecuación diferencial de segundo orden, suponiendo que la altitud y la velocidad del objeto en el tiempo t = 0 sean conocidas. Suponga que la gravedad es la única fuerza que actúa sobre el objeto.

(b) Resuelva el problema de valor inicial deducido en (a) para obtener la altitud en función del tiempo.

Solución:

(a) Sea y(t) la altitud del objeto en el tiempo t. Dado que la aceleración del objeto tiene una magnitud constante g y está en dirección hacia abajo (negativa), y satisface la ecuación de segundo orden

donde las primas ahora indican diferenciación con respecto a t. Si y₀ y v₀ denotan la altitud y la velocidad cuando t = 0, entonces y es una solución del problema del valor inicial

(b) Al integrar (9.1.2_17) dos veces, se obtiene

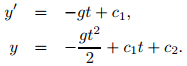
La imposición de las condiciones iniciales y(0) = y₀ e y′(0) = v₀ en estas dos ecuaciones muestra que c₁ = v₀ y c₂ = y₀. Por lo tanto, la solución del problema de valor inicial (9.1.2_17) es

    ♦