| 6.7 Integrales, funciones exponenciales y logaritmos |
Ejercicios propuestos para el Capítulo 6.7
Para los siguientes ejercicios, encuentre la derivada \(\frac{d\mathit{y}}{d\mathit{x}}\):
295. \(\mathit{y} = \ln (2\mathit{x})\)
296. \(\mathit{y} = \ln (2\mathit{x} + 1)\)
297. \(\mathit{y} = \frac{1}{\ln \mathit{x}}\)
Para los siguientes ejercicios, encuentre la integral indefinida:298. \(\int \frac{d\mathit{t}}{3\mathit{t}}\)
299. \(\int \frac{d\mathit{x}}{1 + \mathit{x}}\)
Para los siguientes ejercicios, encuentre la derivada dy/dx. (Puede usar una calculadora para graficar la función y la derivada para confirmar que es correcta):
300. [T] \(\mathit{y} = \frac{\ln(\mathit{x})}{\mathit{x}}\)
301. [T] \(\mathit{y} = \mathit{x} \ln(\mathit{x})\)
302. [T] \(\mathit{y} = \log_{10} \mathit{x}\)
303. [T] \(\mathit{y} = \ln(\sin \mathit{x})\)
304. [T] \(\mathit{y} = \ln(\ln \mathit{x})\)
305. [T] \(\mathit{y} = 7 \ln(4\mathit{x})\)
306. [T] \(\mathit{y} = \ln((4\mathit{x})^7)\)
307. [T] \(\mathit{y} = \ln(\tan \mathit{x})\)
308. [T] \(\mathit{y} = \ln(\tan (3\mathit{x}))\)
309. [T] \(\mathit{y} = \ln(\cos^2 \mathit{x})\)
Para los siguientes ejercicios, encuentre la integral definida o indefinida:
310. \(\int_{0}^{1} \frac{d\mathit{x}}{3 + \mathit{x}}\)
311. \(\int_{0}^{1} \frac{d\mathit{t}}{3 + 2\mathit{t}}\)
312. \(\int_{0}^{2} \frac{\mathit{x} d\mathit{x}}{\mathit{x}^2 + 1}\)
313. \(\int_{0}^{2} \frac{\mathit{x}^3 d\mathit{x}}{\mathit{x}^2 + 1}\)
314. \(\int_{2}^{e} \frac{d\mathit{x}}{\mathit{x} \ln \mathit{x}}\)
315. \(\int_{2}^{e} \frac{d\mathit{x}}{\mathit{x} (\ln \mathit{x})^2}\)
316. \(\int \frac{\cos \mathit{x}}{\sin \mathit{x}} d\mathit{x}\)
317. \(\int_{0}^{\pi/4} \tan \mathit{x} d\mathit{x}\)
318. \(\int \cot (3\mathit{x}) d\mathit{x}\)
319. \(\int \frac{(\ln \mathit{x})^2}{\mathit{x}} d\mathit{x}\)
Para los siguientes ejercicios, calcula \(\frac{d\mathit{y}}{d\mathit{x}}\) diferenciando \(\ln \mathit{y}\):
320. \(\mathit{y} = \sqrt{\mathit{x}^{\,2} + 1}\)
321. \(\mathit{y} = \sqrt{\mathit{x}^{\,2} + 1} \sqrt{\mathit{x}^{\,2} – 1}\)
322. \(\mathit{y} = e^{\sin \mathit{x}}\)
323. \(\mathit{y} = \mathit{x}^{-1/\mathit{x}}\)
324. \(\mathit{y} = e^{(e^{\mathit{x}})}\)
325. \(\mathit{y} = \mathit{x}^{e}\)
326. \(\mathit{y} = \mathit{x}^{(e^{\mathit{x}})}\)
327. \(\mathit{y} = \sqrt{\mathit{x}} \sqrt[3]{\mathit{x}} \sqrt[6]{\mathit{x}}\)
328. \(\mathit{y} = \mathit{x}^{-1/\ln \mathit{x}}\)
329. \(\mathit{y} = e^{-\ln \mathit{x}}\)
Para los siguientes ejercicios, evalúe por cualquier método:
330. \(\int_{5}^{10} \frac{d\mathit{t}}{\mathit{t}} – \int_{5\mathit{x}}^{10\mathit{x}} \frac{d\mathit{t}}{\mathit{t}}\)
331. \(\int_{1}^{e^x} \frac{d\mathit{x}}{\mathit{x}} + \int_{2}^{1} \frac{d\mathit{x}}{\mathit{x}}\)
332. \(\frac{d}{d\mathit{x}} \int_{\mathit{x}}^{1} \frac{d\mathit{t}}{\mathit{t}}\)
333. \(\frac{d}{d\mathit{x}} \int_{\mathit{x}}^{\mathit{x}^2} \frac{d\mathit{t}}{\mathit{t}}\)
334. \(\frac{d}{d\mathit{x}} \ln(\sec \mathit{x} + \tan \mathit{x})\)
Para los siguientes ejercicios, use la función \(\ln \mathit{x}\). Si no puede encontrar los puntos de intersección analíticamente, use una calculadora:
335. Encuentra el área de la región encerrada por \(\mathit{x} = 1\) y \(\mathit{y} = 5\) por encima de \(\mathit{y} = \ln \mathit{x}\).
336. [T] Encuentra la longitud del arco de \(\ln \mathit{x}\) desde \(\mathit{x} = 1\) hasta \(\mathit{x} = 2\).
337. Encuentra el área entre \(\ln \mathit{x}\) y el eje x desde \(\mathit{x} = 1\) hasta \(\mathit{x} = 2\).
338. Encuentra el volumen de la forma creada al rotar esta curva desde \(\mathit{x} = 1\) hasta \(\mathit{x} = 2\) alrededor del eje x, como se muestra aquí.
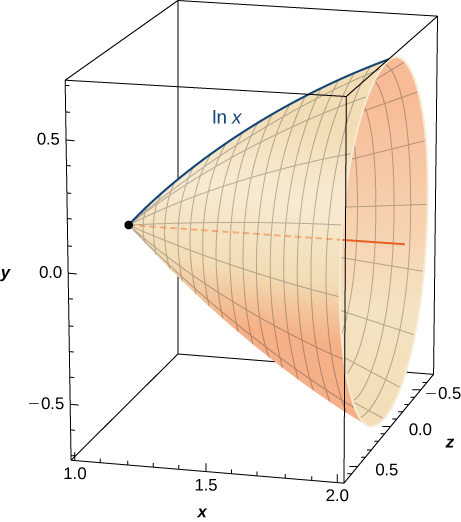
339. [T] Encuentre el área de la superficie de la forma creada al rotar la curva en el ejercicio anterior desde \(\mathit{x} = 1\) hasta \(\mathit{x} = 2\) alrededor del eje \(\mathit{x}\).
Si no puede encontrar los puntos de intersección analíticamente en los siguientes ejercicios, use una calculadora:
340. Encuentra el área del cuarto de círculo hiperbólico encerrado por \(\mathit{x} = 2\) e \(\mathit{y} = 2\) por encima de \(\mathit{y} = 1/\mathit{x}\).
341. [T] Encuentra la longitud del arco de \(\mathit{y} = 1/\mathit{x}\) desde \(\mathit{x} = 1\) hasta \(\mathit{x} = 4\).
342. Encuentra el área debajo de \(\mathit{y} = 1/\mathit{x}\) y por encima del eje x desde \(\mathit{x} = 1\) hasta \(\mathit{x} = 4\).
Para los siguientes ejercicios, verifica las derivadas y antiderivadas.
343. \(\frac{d}{d\mathit{x}} \ln (\mathit{x} + \sqrt{\mathit{x}^{\,2} + 1}) = \frac{1}{\sqrt{1 + \mathit{x}^{\,2}}}\)
344. \(\frac{d}{d\mathit{x}} \ln \left( \frac{\mathit{x} – \mathit{a}}{\mathit{x} + \mathit{a}} \right) = \frac{2\mathit{a}}{(\mathit{x}^2 – \mathit{a}^2)}\)
345. \(\frac{d}{d\mathit{x}} \ln \left( \frac{1 + \sqrt{1 – \mathit{x}^2}}{\mathit{x}} \right) = -\frac{1}{\mathit{x} \sqrt{1 – \mathit{x}^2}}\)
346. \(\frac{d}{d\mathit{x}} \ln (\mathit{x} + \sqrt{\mathit{x}^{\,2} – \mathit{a}^2}) = \frac{1}{\sqrt{\mathit{x}^{\,2} – \mathit{a}^2}}\)
347. \(\int \frac{d\mathit{x}}{\mathit{x} \ln \mathit{x} \ln (\ln \mathit{x})} = \ln (\ln (\ln \mathit{x})) + C\)
