| 6.6 Momentos y centros de masa |
Ejercicios propuestos para el Capítulo 6.6
Para los siguientes ejercicios, calcule el centro de masa para la colección de masas dada:
254. \(\mathit{m}_1 = 2\) en \(\mathit{x}_1 = 1\) y \(\mathit{m}_2 = 4\) en \(\mathit{x}_2 = 2\)
255. \(\mathit{m}_1 = 1\) en \(\mathit{x}_1 = -1\) y \(\mathit{m}_2 = 3\) en \(\mathit{x}_2 = 2\)
256. \(\mathit{m} = 3\) en \(\mathit{x} = 0, 1, 2, 6\)
257. Masas unitarias en \((\mathit{x}, \mathit{y}) = (1, 0), (0, 1), (1, 1)\)
258. \(\mathit{m}_1 = 1\) en \((1, 0)\) y \(\mathit{m}_2 = 4\) en \((0, 1)\)
259. \(\mathit{m}_1 = 1\) en \((1, 0)\) y \(\mathit{m}_2 = 3\) en \((2, 2)\)
Para los siguientes ejercicios, calcule el centro de masa \(\overline{x}\):
260. \(\rho = 1\) para \(\mathit{x} \in (-1, 3)\)
261. \(\rho = \mathit{x}^2\) para \(\mathit{x} \in (0, \mathit{L})\)
262. \(\rho = 1\) para \(\mathit{x} \in (0, 1)\) y \(\rho = 2\) para \(\mathit{x} \in (1, 2)\)
263. \(\rho = \sin \mathit{x}\) para \(\mathit{x} \in (0, \pi)\)
264. \(\rho = \cos \mathit{x}\) para \(\mathit{x} \in (0, \frac{\pi}{2})\)
265. \(\rho = e^{\mathit{x}}\) para \(\mathit{x} \in (0, 2)\)
266. \(\rho = \mathit{x}^3 + \mathit{x}e^{-\mathit{x}}\) para \(\mathit{x} \in (0, 1)\)
267. \(\rho = \mathit{x} \sin \mathit{x}\) para \(\mathit{x} \in (0, \pi)\)
268. \(\rho = \sqrt{\mathit{x}}\) para \(\mathit{x} \in (1, 4)\)
269. \(\rho = \ln \mathit{x}\) para \(\mathit{x} \in (1, e)\)
Para los siguientes ejercicios, calcule el centro de masa \((\overline{\mathit{x}}, \overline{\mathit{y}})\). Use la simetría para ayudar a localizar el centro de masa siempre que sea posible:
270. \(\rho = 7\) en el cuadrado \(0 \leq \mathit{x} \leq 1, 0 \leq \mathit{y} \leq 1\)
271. \(\rho = 3\) en el triángulo con vértices \((0, 0), (\mathit{a}, 0)\), y \((0, \mathit{b})\)
272. \(\rho = 2\) para la región acotada por \(\mathit{y} = \cos(\mathit{x})\), \(\mathit{y} = -\cos(\mathit{x})\), \(\mathit{x} = -\frac{\pi}{2}\), y \(\mathit{x} = \frac{\pi}{2}\)
Para los siguientes ejercicios, use una calculadora para dibujar la región, luego calcule el centro de masa \((\overline{\mathit{x}}, \overline{\mathit{y}})\). Use la simetría para ayudar a localizar el centro de masa siempre que sea posible:
273. [T] La región acotada por \(\mathit{y} = \cos(2\mathit{x})\), \(\mathit{x} = -\frac{\pi}{4}\), y \(\mathit{x} = \frac{\pi}{4}\)
274. [T] La región entre \(\mathit{y} = 2\mathit{x}^2\), \(\mathit{y} = 0\), \(\mathit{x} = 0\), y \(\mathit{x} = 1\)
275. [T] La región entre \(\mathit{y} = \frac{5}{4} \mathit{x}^2\) e \(\mathit{y} = 5\)
276. [T] Región entre \(\mathit{y} = \sqrt{\mathit{x}}\), \(\mathit{y} = \ln(\mathit{x})\), \(\mathit{x} = 1\), y \(\mathit{x} = 4\)
277. [T] La región acotada por \(\mathit{y} = 0\), \(\frac{\mathit{x}^2}{4} + \frac{\mathit{y}^2}{9} = 1\)
278. [T] La región acotada por \(\mathit{y} = 0\), \(\mathit{x} = 0\), y \(\frac{\mathit{x}^2}{4} + \frac{\mathit{y}^2}{9} = 1\)
279. [T] La región acotada por \(\mathit{y} = \mathit{x}^2\) e \(\mathit{y} = \mathit{x}^4\) en el primer cuadrante
Para los siguientes ejercicios, use el teorema de Pappus para determinar el volumen de la forma:
280. Rotando \(\mathit{y} = \mathit{mx}\) alrededor del eje \(\mathit{x}\) entre \(\mathit{x} = 0\) y \(\mathit{x} = 1\)
281. Rotando \(\mathit{y} = \mathit{mx}\) alrededor del eje \(\mathit{y}\) entre \(\mathit{x} = 0\) y \(\mathit{x} = 1\)
282. Un cono general creado al rotar un triángulo con vértices \((0, 0), (\mathit{a}, 0)\), y \((0, \mathit{b})\) alrededor del eje \(\mathit{y}\). ¿Concuerda tu respuesta con el volumen de un cono?
283. Un cilindro general creado al rotar un rectángulo con vértices \((0, 0), (\mathit{a}, 0), (0, \mathit{b})\), y \((\mathit{a}, \mathit{b})\) alrededor del eje \(\mathit{y}\). ¿Concuerda tu respuesta con el volumen de un cilindro?
284. Una esfera creada al rotar un semicírculo con radio \(\mathit{a}\) alrededor del eje \(\mathit{y}\). ¿Concuerda tu respuesta con el volumen de una esfera?
Para los siguientes ejercicios, use una calculadora para dibujar la región encerrada por la curva. Encuentra el área \(\mathit{M}\) y el centroide \((\overline{\mathit{x}}, \overline{\mathit{y}})\) para las formas dadas. Use la simetría para ayudar a localizar el centro de masa siempre que sea posible:
285. [T] Cuarto de círculo: \(\mathit{y} = \sqrt{1 – \mathit{x}^2}\), \(\mathit{y} = 0\), y \(\mathit{x} = 0\)
286. [T] Triángulo: \(\mathit{y} = \mathit{x}\), \(\mathit{y} = 2 – \mathit{x}\), y \(\mathit{y} = 0\)
287. [T] Lente: \(\mathit{y} = \mathit{x}^2\) e \(\mathit{y} = \mathit{x}\)
288. [T] Anillo: \(\mathit{y}^2 + \mathit{x}^2 = 1\) e \(\mathit{y}^2 + \mathit{x}^2 = 4\)
289. [T] Semi-anillo: \(\mathit{y}^2 + \mathit{x}^2 = 1\), \(\mathit{y}^2 + \mathit{x}^2 = 4\), y \(\mathit{y} = 0\)
290. Encuentre el centro de masa generalizado en la astilla entre \(\mathit{y} = \mathit{x}^a\) e \(\mathit{y} = \mathit{x}^b\) con \(\mathit{a} > \mathit{b}\). Luego, use el teorema de Pappus para encontrar el volumen del sólido generado al girar alrededor del eje \(\mathit{y}\).
291. Encuentre el centro de masa generalizado entre \(\mathit{y} = \mathit{a}^2 – \mathit{x}^2\), \(\mathit{x} = 0\), e \(\mathit{y} = 0\). Luego, use el teorema de Pappus para encontrar el volumen del sólido generado al girar alrededor del eje \(\mathit{y}\).
292. Encuentre el centro de masa generalizado entre \(\mathit{y} = \mathit{b} \sin(\mathit{ax})\), \(\mathit{x} = 0\), y \(\mathit{x} = \frac{\pi}{\mathit{a}}\). Luego, use el teorema de Pappus para encontrar el volumen del sólido generado al girar alrededor del eje \(\mathit{y}\).
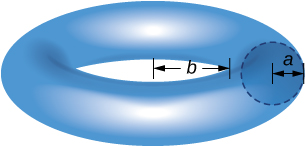
293. Use el teorema de Pappus para encontrar el volumen de un toro (que se muestra aquí). Asuma que un disco de radio \(\mathit{a}\) se coloca con el extremo izquierdo del círculo en \(\mathit{x} = \mathit{b}\), \(\mathit{b} > 0\), y se gira alrededor del eje \(\mathit{y}\).
294. Encuentre el centro de masa \((\overline{\mathit{x}}, \overline{\mathit{y}})\) para un alambre delgado a lo largo del semicírculo \(\mathit{y} = \sqrt{1 – \mathit{x}^2}\) con masa unitaria. (Pista: Use el teorema de Pappus.)
