| 9. Ecuaciones diferenciales | 9.6 Aplicaciones de ecuaciones lineales de segundo orden | Ejercicios propuestos para el Capítulo 9.6.2 |

9.6.2 PROBLEMAS DE MUELLES II

Vibraciones libres con amortiguación

En esta sección consideramos el movimiento de un objeto en un sistema masa-resorte con amortiguamiento. Comenzamos con movimiento no forzado, por lo que la ecuación de movimiento es

my′′ + cy′ + ky = 0.         (9.6.2.1)

Ahora suponga que el objeto se desplaza del equilibrio y se le da una velocidad inicial. La intuición sugiere que si la fuerza de amortiguamiento es lo suficientemente débil, el movimiento resultante será oscilatorio, como en el caso no amortiguado considerado en la sección anterior, mientras que si es lo suficientemente fuerte, el objeto puede moverse lentamente hacia la posición de equilibrio sin llegar a alcanzarla. Ahora confirmaremos matemáticamente estas ideas intuitivas. La ecuación característica de (9.6.2.1) es

mr² + cr + k = 0.

Las raíces de esta ecuación son

  y          (9.6.2.2)

En la Sección 9.5.2 vimos que la forma de la solución de (9.6.2.1) depende de si c² − 4mk es positivo, negativo o cero. Ahora consideraremos estos tres casos.

Movimiento subamortiguado

Decimos que el movimiento está subamortiguado si c < √(4mk). En este caso, r₁ y r₂ en (9.6.2.2) son conjugados complejos, que escribimos como

  y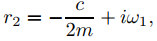 

donde

La solución general de (9.6.2.1) en este caso es

Por el método usado en la Sección 9.6.1 para derivar la forma amplitud-fase del desplazamiento de un objeto en movimiento armónico simple, podemos reescribir esta ecuación como

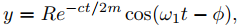        (9.6.2.3)

donde

Rcosφ = c₁, y  Rsenφ = c₂.

El factor Re^−ct/2m en (9.6.2.3) se denomina amplitud del movimiento variable en el tiempo, la cantidad ω1 se denomina frecuencia y T = 2π/ω₁ (que es el período de la función coseno en (9.6 .2.3) se denomina cuasi-período. En la figura 9.6.2.1 se muestra una gráfica típica de (9.6.2.3). Como se ilustra en esa figura, la gráfica de y oscila entre las curvas exponenciales punteadas y = ±Re^−ct/2m.

Figura 9.6.2.1 Movimiento subamortiguado

Movimiento sobreamortiguado

Decimos que el movimiento está sobreamortiguado si c > √(4mk). En este caso los ceros r₁ y r₂ del polinomio característico son reales, con r1r₁ < r₂ < 0 (ver (9.6.2.2)), y la solución general de (9.6.2.1) es

De nuevo lím_t→∞ y(t) = 0 como en el caso subamortiguado, pero el movimiento no es oscilatorio, ya que y no puede ser igual a cero para más de un valor de t a menos que c₁ = c₂ = 0. (Ejercicio 23).

Movimiento críticamente amortiguado

Decimos que el movimiento está críticamente amortiguado si c = √(4mk). En este caso r₁ = r₂ = −c/2m y la solución general de (9.6.2.1) es

Nuevamente lim_t→∞ y(t) = 0 y el movimiento no es oscilatorio, ya que y no puede ser igual a cero para más de un valor de t a menos que c₁ = c₂ = 0. (Ejercicio 22).

Ejemplo ilustrativo 9.6.2.1

Suponga que un peso de 64 lb estira un resorte 6 pulgadas en equilibrio y un amortiguador proporciona una fuerza de amortiguamiento de c lb por cada pie/seg de velocidad.

(a) Escriba la ecuación de movimiento del objeto y determine el valor de c para el cual el movimiento está críticamente amortiguado.
(b) Encuentre el desplazamiento y para t > 0 si el movimiento está críticamente amortiguado y las condiciones iniciales son y(0) = 1 y y′(0) = 20.
(c) Halle el desplazamiento y para t > 0 si el movimiento está críticamente amortiguado y las condiciones iniciales son y(0) = 1 y y′(0) = −20.

Solución:

(a) Aquí m = 2 slugs y k = 64/0.5 = 128 lb/ft. Por tanto, la ecuación de movimiento (9.6.2.1) es

2y′′ + cy′ + 128y = 0.         (9.6.2.4)

La ecuación característica es

2r² + cr + 128 = 0,

que tiene raíces

Por lo tanto, el amortiguamiento es crítico si

c = √(8 · 128) = 32 lb–seg/pie.

(b) Al establecer c = 32 en (9.6.2.4) y cancelar el factor común 2 se obtiene

y′′ + 16y + 64y = 0.

La ecuación característica es

r² + 16r + 64y = (r + 8)² = 0.

Por lo tanto, la solución general es

y = e^−8t(c₁ + c₂t).         (9.6.2.5)

Diferenciando esto se obtiene

y′ = −8y + c₂e^−8t.         (9.6.2.6)

La imposición de las condiciones iniciales y(0) = 1 y y′(0) = 20 en las dos últimas ecuaciones muestra que 1 = c₁ y 20 = −8 + c₂. Por lo tanto, la solución del problema de valor inicial es

y = e^−8t(1 + 28t).

Por lo tanto, el objeto se aproxima al equilibrio desde arriba cuando t → ∞. No hay oscilación.

Figura 9.6.2.2 (a) y = e^−8t(1 + 28t)  (b) y = e^−8t(1 + 28t)

(c) Al imponer las condiciones iniciales y(0) = 1 y y′(0) = −20 en (9.6.2.5) y (9.6.2.6) se obtiene 1 = c₁ y −20 = −8 + c₂. Por lo tanto, la solución de este problema de valor inicial es

y = e^−8t(1 − 12t).

Por lo tanto, el objeto se mueve hacia abajo a través del equilibrio solo una vez y luego se acerca al equilibrio desde abajo cuando t → ∞. De nuevo, no hay oscilación. Las soluciones de estos dos problemas de valor inicial se representan gráficamente en la figura 9.6.2.2.  ♦

Ejemplo ilustrativo 9.6.2.2

Encuentre el desplazamiento del objeto en el Ejemplo 6.2.1 si la constante de amortiguamiento es c = 4 lb–seg/ft y las condiciones iniciales son y(0) = 1.5 ft y y′(0) = −3 ft/seg.

Solución:

Con c = 4, la ecuación de movimiento (9.6.2.4) se convierte en

y′′ + 2y′ + 64y = 0         (9.6.2.7)

después de cancelar el factor común 2. La ecuación característica

 r² + 2r + 64 = 0

tiene raíces complejas conjugadas

Por tanto, el movimiento está subamortiguado y la solución general de (9.6.2.7) es

y = e^−t(c₁cos 3√7t + c₂ sen3√7t).

Diferenciando esto se obtiene

y′ = − y + 3√7e^−t(−c₁ sen 3√7t + c₂ cos 3√7t).

Al imponer las condiciones iniciales y(0) = 1,5 y y′(0) = −3 en las dos últimas ecuaciones se obtiene 1,5 = c₁ y −3 = −1,5 + 3√7c₂. Por lo tanto, la solución del problema de valor inicial es

         (9.6.2.8)

La amplitud de la función entre paréntesis es

Por lo tanto podemos reescribir (9.6.2.8) como

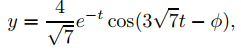
donde

  y 

Por lo tanto φ ≅ −0.125 radianes.  ♦

Ejemplo ilustrativo 9.6.2.3

Sea la constante de amortiguamiento en el Ejemplo 1 c = 40 lb-seg/ft. Encuentre el desplazamiento y para t > 0 si y(0) = 1 y y′(0) = 1.

Solución:

Con c = 40, la ecuación de movimiento (9.6.2.4) se reduce a

y′′ + 20y′ + 64y = 0          (9.6.2.9)

después de cancelar el factor común 2. La ecuación característica

r² + 20r + 64 = (r + 16)(r + 4) = 0

tiene las raíces r₁ = −4 y r₂ = −16. Por tanto, la solución general de (9.6.2.9) es

y = c₁e^−4t + c₂e^−16t.         (9.6.2.10)

Diferenciando esto se obtiene

y′ = −c₁4e^−4t − 16c₂e^−16t.

Las dos últimas ecuaciones y las condiciones iniciales y(0) = 1 y y′(0) = 1 implican que

La solución de este sistema es c₁ = 17/12, c₂ = −5/12. Sustituyendo estos en (9.6.2.10) se obtiene

como la solución del problema de valor inicial dado (Figura 9.6.2.3).  ♦

Figura 9.6.2.3

Vibraciones Forzadas Con Amortiguación

Ahora consideramos el movimiento de un objeto en un sistema masa-resorte con amortiguamiento, bajo la influencia de una función forzada periódica F(t) = F₀ cosωt, de modo que la ecuación de movimiento es

my′′ + cy′ + ky = F₀ cosωt.         (9.6.2.11)

En la Sección 9.6.1 consideramos esta ecuación con c = 0 y encontramos que el desplazamiento resultante y asumía valores arbitrariamente grandes en el caso de resonancia (es decir, cuando ω = ω₀ = √k/m). Aquí veremos que en presencia de amortiguamiento el desplazamiento permanece acotado para todo t, y las condiciones iniciales tienen poco efecto sobre el movimiento cuando t → ∞. De hecho, veremos que para t grande, el desplazamiento se aproxima mucho mediante una función de la forma

y = R cos(ωt − φ),         (9.6.2.12)

donde la amplitud R depende de m, c, k, F₀ y ω. Nos interesa la siguiente pregunta:

PREGUNTA: Suponiendo que m, c, k y F₀ se mantienen constantes, ¿qué valor de ω produce la mayor amplitud R en (9.6.2.12), y cuál es esta mayor amplitud?

       Para responder a esta pregunta, debemos resolver (9.6.2.11) y determinar R en términos de F₀, ω₀, ω y c. Podemos obtener una solución particular de (9.6.2.11) por el método de los coeficientes indeterminados. Como cos ωt no satisface la ecuación complementaria

my′′ + cy′ + ky = 0,

podemos obtener una solución particular de (9.6.2.11) en la forma

y_p = Acosωt + Bsenωt.         (9.6.2.13)

Diferenciando esto se obtiene

y_p′ = ω(−Asenωt + Bcosωt)

y

y_p′′ = −ω²(Acosωt + Bsenωt).

De las últimas tres ecuaciones,

my_p′′ + cy_p′ + ky_p = (−mω²A + cωB + kA) cosωt + (−mω²B − cωA + kB) senωt,

entonces y_p satisface (9.6.2.11) si

Resolviendo para A y B y sustituyendo los resultados en (9.6.2.13) se obtiene

que se puede escribir en forma de amplitud-fase como

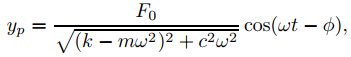        (9.6.2.14)

donde

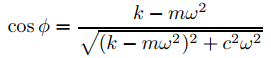  y          (9.6.2.15)

       Para comparar esto con la vibración forzada no amortiguada que consideramos en la Sección 9.6.1, es útil escribir

        (9.6.2.16)

donde ω₀ = √k/m es la frecuencia angular natural del movimiento armónico simple no amortiguado de un objeto con masa m sobre un resorte con constante k. Sustituyendo (9.6.2.16) en (9.6.2.14) se obtiene

      (9.6.2.17)

      La solución de un problema de valor inicial

my′′ + cy′ + ky = F₀ cosωt,  y(0) = y₀,  y′(0) = v₀,

es de la forma y = y_c + y_p, donde y_c tiene una de las tres formas

En los tres casos lim_t→∞ y_c(t) = 0 para cualquier elección de c₁ y c₂. Por eso decimos que y_c  es la componente transitoria de la solución y. El comportamiento de y para t grande está determinado por y_p, que llamamos componente de estado estacionario de y. Por lo tanto, para t grande, el movimiento es como un movimiento armónico simple a la frecuencia de la fuerza externa.

      La amplitud de y_p en (9.6.2.17) es

        (9.6.2.18)

que es finito para todo ω; es decir, la presencia de amortiguamiento excluye el fenómeno de resonancia que encontramos al estudiar vibraciones no amortiguadas bajo una función forzada periódica. Ahora encontraremos el valor ω_max de ω para el cual R se maximiza. Este es el valor de ω para el cual la función

ρ(ω) = m²(ω₀² − ω²)² + c²ω²

en el denominador de (9.6.2.18) alcanza su valor mínimo. Al reescribir esto como

ρ(ω) = m²(ω₀⁴ + ω⁴) + (c² − 2m²ω₀²)ω²,          (6.2.19)

se puede ver que ρ es una función estrictamente creciente de ω² si

(Recordemos que ω₀² = k/m). Por lo tanto ω_max = 0 si se cumple esta desigualdad. De (9.6.2.15), puedes ver que φ = 0 si ω = 0. En este caso, (9.6.2.14) se reduce a

lo cual es consistente con la ley de Hooke: si la masa está sujeta a una fuerza constante F₀, su desplazamiento debe aproximarse a una constante y_p tal que ky_p = F₀. Ahora suponga que c < √2mk. Entonces, de (9.6.2.19),

ρ′(ω) = 2ω(2m²ω² + c² − 2m²ω₀²),

y ω_max es el valor de ω para el cual la expresión entre paréntesis es igual a cero; es decir,

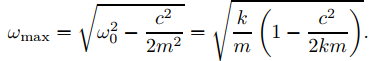
(Para ver que ρ(ω_max) es el valor mínimo de ρ(ω), tenga en cuenta que ρ′(ω) < 0 si ω < ω_max y ρ′(ω) > 0 si ω > ω_max.) Sustituyendo ω = ω_max en (9.6.2.18) y simplificando muestra que la amplitud máxima R_max es

  si 

Resumimos nuestros resultados de la siguiente manera.

Teorema 9.6.2.1

Supongamos que consideramos la amplitud R de la componente de estado estacionario de la solución de

my′′ + cy′ + ky = F₀ cosωt

en función de ω.

(a) Si c ≥ √(2mk), la amplitud máxima es R_max = F₀/k y se alcanza cuando ω = ω_max = 0.
(b) Si c < √(2mk), la amplitud máxima es

      (6.2.20)

y se logra cuando

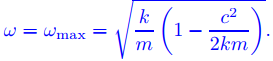      (6.2.21)

Nótese que R_max y ω_max son funciones continuas de c, para c ≥ 0, ya que (9.6.2.20) y (9.6.2.21) se reducen a R_max = F₀/k y ω_max = 0 si c = √(2km).  ♦