| 11. Diferenciación de funciones de varias variables | Ejercicios propuestos para el Capítulo 11.4 |

11.4 Planos tangentes y aproximaciones lineales

Objetivos de aprendizaje

En esta sección consideramos el problema de hallar el plano tangente a una superficie, lo cual es análogo a encontrar la ecuación de la recta tangente a una curva cuando la curva está definida por la gráfica de una función de una sola variable, y = f (x). La pendiente de la recta tangente en el punto (x = a) viene dada por m = f ′(a); ¿cuál es entonces la pendiente de un plano tangente? Ya hemos estudiado la ecuación de un plano en Ecuaciones de rectas y planos en el espacio; en esta sección veremos cómo puede aplicarse al problema que nos ocupa.

Planos tangentes

De manera intuitiva, parece claro que, en un plano, solo una recta puede ser tangente a una curva en un punto. Sin embargo, en el espacio tridimensional, muchas rectas pueden ser tangentes en un punto dado. Si estas rectas se encuentran en un mismo plano, determinan el plano tangente en ese punto. Un plano tangente en un punto regular contiene todas las rectas tangentes en ese punto.

Una forma más intuitiva de pensar en un plano tangente es suponer que la superficie es suave en ese punto (sin esquinas). Entonces, una recta tangente a la superficie en ese punto, en cualquier dirección, no presenta cambios bruscos en la pendiente, ya que la dirección varía de manera suave.

Definición

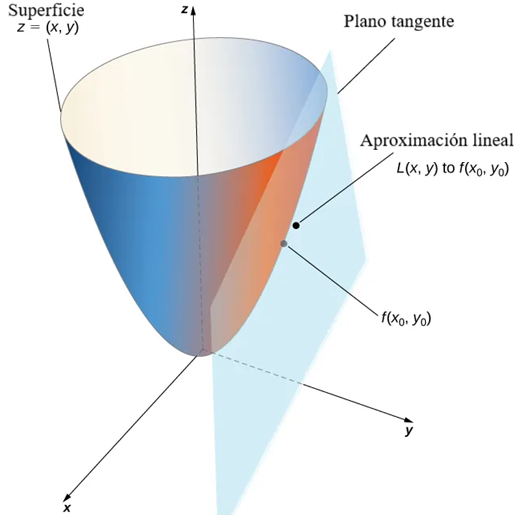
Sea $P_0 = (x_0, y_0, z_0)$ un punto en una superficie $S$, y sea $C$ cualquier curva que pase por $P_0$ y se encuentre enteramente en $S$. Si las líneas tangentes a todas estas curvas $C$ en $P_0$ se encuentran en el mismo plano, entonces este plano se llama el plano tangente a $S$ en $P_0$ (Figura 11.4.1).

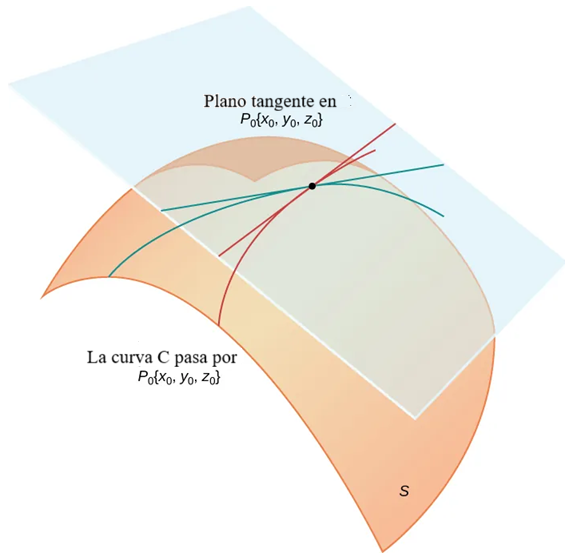
Figura 11.4.1 El plano tangente a una superficie 𝑆 en un punto 𝑃0 contiene todas las rectas tangentes a las curvas en 𝑆 que pasan por 𝑃0.

Para que exista un plano tangente a una superficie en un punto de dicha superficie, es suficiente que la función que define la superficie sea diferenciable en ese punto, como se definirá más adelante en esta sección. Aquí definimos el término plano tangente y luego exploramos la idea de manera intuitiva.

Definición

Sea $S$ una superficie definida por una función diferenciable $z = f(x, y)$, y sea $P_0 = (x_0, y_0)$ un punto en el dominio de $f$. Entonces, la ecuación del plano tangente a $S$ en $P_0$ está dada por

$$ z = f(x_0, y_0) + f_x(x_0, y_0)(x – x_0) + f_y(x_0, y_0)(y – y_0). \hspace{20pt} \text{(11.4.1)}$$

♦

Para ver por qué esta fórmula es correcta, primero busquemos dos líneas tangentes a la superficie $S$. La ecuación de la línea tangente a la curva representada por la intersección de $S$ con la traza vertical dada por $x = x_0$ es $z = f(x_0, y_0) + f_y(x_0, y_0)(y – y_0)$. De manera similar, la ecuación de la línea tangente a la curva representada por la intersección de $S$ con la traza vertical dada por $y = y_0$ es $z = f(x_0, y_0) + f_x(x_0, y_0)(x – x_0)$. Un vector paralelo a la primera línea tangente es $\mathbf{a} = \mathbf{j} + f_y(x_0, y_0)\mathbf{k}$; un vector paralelo a la segunda línea tangente es $\mathbf{b} = \mathbf{i} + f_x(x_0, y_0)\mathbf{k}$. Podemos realizar el producto cruz de estos dos vectores:

$$ \begin{aligned} \mathbf{a} \times \mathbf{b} &= (\mathbf{j} + f_y(x_0, y_0)\mathbf{k}) \times (\mathbf{i} + f_x(x_0, y_0)\mathbf{k}) \\ &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 1 & f_y(x_0, y_0) \\ 1 & 0 & f_x(x_0, y_0) \end{vmatrix} \\ &= f_x(x_0, y_0)\mathbf{i} + f_y(x_0, y_0)\mathbf{j} – \mathbf{k}. \end{aligned} $$

Este vector es perpendicular a ambas líneas y, por lo tanto, es perpendicular al plano tangente. Podemos usar este vector como un vector normal al plano tangente, junto con el punto $P_0 = (x_0, y_0, f(x_0, y_0))$ en la ecuación para un plano:

$$ \begin{aligned} \mathbf{n} \cdot ((x – x_0)\mathbf{i} + (y – y_0)\mathbf{j} + (z – f(x_0, y_0))\mathbf{k}) &= 0 \\ (f_x(x_0, y_0)\mathbf{i} + f_y(x_0, y_0)\mathbf{j} – \mathbf{k}) \cdot ((x – x_0)\mathbf{i} + (y – y_0)\mathbf{j} + (z – f(x_0, y_0))\mathbf{k}) &= 0 \\ f_x(x_0, y_0)(x – x_0) + f_y(x_0, y_0)(y – y_0) – (z – f(x_0, y_0)) &= 0. \end{aligned} $$

Al resolver esta ecuación para (z) se obtiene la Ecuación 11.4.1.

Ejemplo ilustrativo 11.4.1. Determinación de un plano tangente

Halle la ecuación del plano tangente a la superficie definida por la función

$$ f(x, y) = 2x^2 – 3xy + 8y^2 + 2x – 4y + 4 \text{ en el punto } (2, -1). $$

Solución:

Primero, debemos calcular $f_x (x, y)$ y $f_y (x, y)$, luego utilizar la Ecuación 11.4.1 con $x_0 = 2$ y $y_0 = -1$:

$$ \begin{aligned} f_x (x, y) &= 4x – 3y + 2 \\ f_y (x, y) &= -3x + 16y – 4 \\ f(2, -1) &= 2(2)^2 – 3(2)(-1) + 8(-1)^2 + 2(2) – 4(-1) + 4 = 34 \\ f_x (2, -1) &= 4(2) – 3(-1) + 2 = 13 \\ f_y (2, -1) &= -3(2) + 16(-1) – 4 = -26 \end{aligned} $$

Entonces, la Ecuación 11.4.1 se convierte en

$$ \begin{aligned} z &= f(x_0, y_0) + f_x (x_0, y_0)(x – x_0) + f_y (x_0, y_0)(y – y_0) \\ z &= 34 + 13(x – 2) – 26(y – (-1)) \\ z &= 34 + 13x – 26 – 26y – 26 \\ z &= 13x – 26y – 18 \end{aligned} $$

(Vea la siguiente figura).

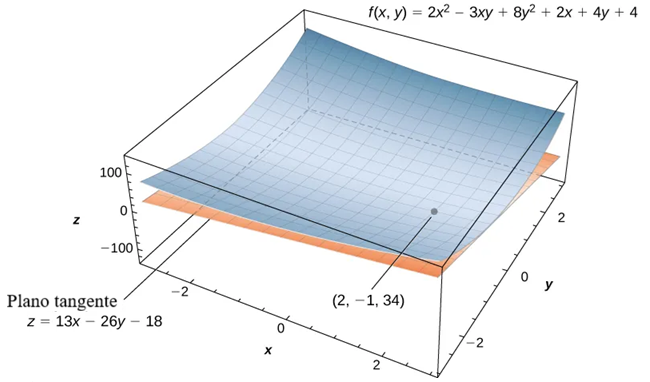
Figura 11.4.2 Cálculo de la ecuación de un plano tangente a una superficie dada en un punto dado.

Ejercicio de control 11.4.1

Halle la ecuación del plano tangente a la superficie definida por la función:

$$f(x, y) = x^3 – x^2y + y^2 – 2x + 3y – 2 \text{ en el punto } (-1, 3).$$
♦

Ejemplo ilustrativo 11.4.2. Determinación de otro plano tangente

Halle la ecuación del plano tangente a la superficie definida por la función

$$f(x, y) = \sin (2x) \cos (3y) \text{ en el punto } (\pi/3, \pi/4).$$

Solución:

Primero, calcule $f_x(x, y)$ y $f_y(x, y)$, luego use la Ecuación 11.4.1 con $x_0 = \pi/3$ y $y_0 = \pi/4$:

$$ \begin{aligned} f_x(x, y) &= 2 \cos (2x) \cos (3y) \\ f_y(x, y) &= -3 \sin (2x) \sin (3y) \\ f\left(\frac{\pi}{3}, \frac{\pi}{4}\right) &= \sin \left(2 \left(\frac{\pi}{3}\right)\right) \cos \left(3 \left(\frac{\pi}{4}\right)\right) = \left(\frac{\sqrt{3}}{2}\right) \left(-\frac{\sqrt{2}}{2}\right) = -\frac{\sqrt{6}}{4} \\ f_x\left(\frac{\pi}{3}, \frac{\pi}{4}\right) &= 2 \cos \left(2 \left(\frac{\pi}{3}\right)\right) \cos \left(3 \left(\frac{\pi}{4}\right)\right) = 2 \left(-\frac{1}{2}\right) \left(-\frac{\sqrt{2}}{2}\right) = \frac{\sqrt{2}}{2} \\ f_y\left(\frac{\pi}{3}, \frac{\pi}{4}\right) &= -3 \sin \left(2 \left(\frac{\pi}{3}\right)\right) \sin \left(3 \left(\frac{\pi}{4}\right)\right) = -3 \left(\frac{\sqrt{3}}{2}\right) \left(\frac{\sqrt{2}}{2}\right) = -\frac{3\sqrt{6}}{4}. \end{aligned} $$

Entonces la Ecuación 11.4.1 se convierte en:

$$ \begin{aligned} z &= f(x_0, y_0) + f_x(x_0, y_0)(x – x_0) + f_y(x_0, y_0)(y – y_0) \\ z &= -\frac{\sqrt{6}}{4} + \frac{\sqrt{2}}{2} \left(x – \frac{\pi}{3}\right) – \frac{3\sqrt{6}}{4} \left(y – \frac{\pi}{4}\right) \\ z &= \frac{\sqrt{2}}{2}x – \frac{3\sqrt{6}}{4}y – \frac{\sqrt{6}}{4} – \frac{\pi\sqrt{2}}{6} + \frac{3\pi\sqrt{6}}{16}. \end{aligned} $$

♦

Un plano tangente a una superficie no siempre existe en cada punto de la superficie. Considere la función

$$f(x, y) = \begin{cases} \frac{xy}{\sqrt{x^2+y^2}} & (x,y) \neq (0,0) \\ 0 & (x,y) = (0,0). \end{cases}$$

La gráfica de esta función se muestra a continuación.

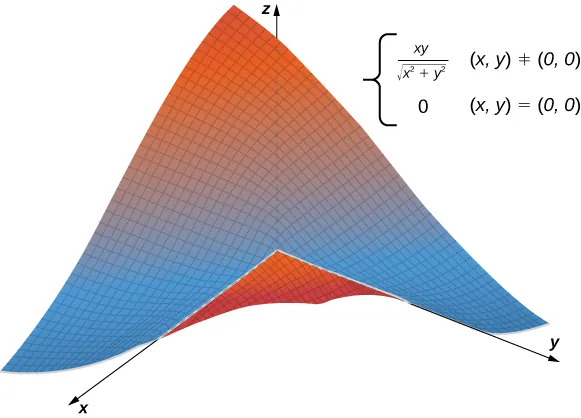
Figura 11.4.3 Gráfica de una función que no tiene plano tangente en el origen.

Si $x = 0$ o $y = 0$, entonces $f(x, y) = 0$, por lo que el valor de la función no cambia en ninguno de los ejes $x$ o $y$. Por lo tanto, $f_x(x, 0) = f_y(0, y) = 0$, de modo que a medida que $x$ o $y$ se acercan a cero, estas derivadas parciales se mantienen iguales a cero. Al sustituirlas en la Ecuación 11.4.1 , se obtiene $z = 0$ como la ecuación de la línea tangente. Sin embargo, si nos acercamos al origen desde una dirección diferente, obtenemos una historia distinta. Por ejemplo, supongamos que nos acercamos al origen a lo largo de la línea $y = x$. Si sustituimos $y = x$ en la función original, se convierte en

$$f(x, x) = \frac{x(x)}{\sqrt{x^2 + (x)^2}} = \frac{x^2}{\sqrt{2x^2}} = \frac{|x|}{\sqrt{2}}.$$

Cuando $x > 0$, la pendiente de esta curva es igual a $\sqrt{2}/2$; cuando $x < 0$, la pendiente de esta curva es igual a $-(\sqrt{2}/2)$. Esto presenta un problema. En la definición de plano tangente, presuponemos que todas las líneas tangentes que pasan por el punto $P$ (en este caso, el origen) se encuentran en el mismo plano. Claramente, este no es el caso aquí. Cuando estudiemos funciones diferenciables, veremos que esta función no es diferenciable en el origen.

Aproximaciones lineales

Recuerde de Aproximaciones Lineales y Diferenciales que la fórmula para la aproximación lineal de una función $f(x)$ en el punto $x = a$ viene dada por

$$y \approx f(a) + f'(a)(x – a).$$

El diagrama de la aproximación lineal de una función de una variable aparece en la siguiente gráfica.

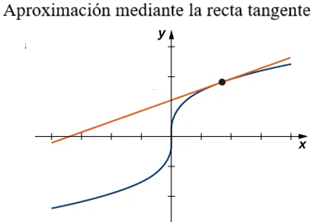
Figura 11.4.4 Aproximación lineal de una función de una variable.

La recta tangente puede utilizarse como una aproximación de la función $f(x)$ para valores de $x$ razonablemente cercanos a $x = a$. Cuando se trabaja con una función de dos variables, la recta tangente se sustituye por un plano tangente, pero la idea de la aproximación es muy similar.

Definición

Dada una función $z = f(x, y)$ con derivadas parciales continuas que existen en el punto $(x_0, y_0)$, la aproximación lineal de $f$ en el punto $(x_0, y_0)$ viene dada por la ecuación

$$L(x, y) = f(x_0, y_0) + f_x(x_0, y_0)(x – x_0) + f_y(x_0, y_0)(y – y_0). \hspace{20pt} \text{(11.4.2)} $$

♦

Observe que esta ecuación también representa el plano tangente a la superficie definida por $z = f(x, y)$ en el punto $(x_0, y_0)$. La idea detrás del uso de una aproximación lineal es que, si hay un punto $(x_0, y_0)$ en el cual se conoce el valor preciso de $f(x, y)$, entonces para valores de $(x, y)$ razonablemente cercanos a $(x_0, y_0)$, la aproximación lineal (es decir, el plano tangente) produce un valor que también está razonablemente cerca del valor exacto de $f(x, y)$ (Figura 11.4.5). Además, el plano que se utiliza para hallar la aproximación lineal es también el plano tangente a la superficie en el punto $(x_0, y_0)$.

Figura 11.4.5 Uso de un plano tangente para la aproximación lineal en un punto.

Ejemplo ilustrativo 11.4.3. Uso de una aproximación mediante el plano tangente

Dada la función $f(x, y) = \sqrt{41 – 4x^2 – y^2}$, aproxime $f(2.1, 2.9)$ utilizando el punto $(2, 3)$ para $(x_0, y_0)$. ¿Cuál es el valor aproximado de $f(2.1, 2.9)$ con cuatro decimales?

Solución:

Para aplicar la Ecuación 11.4.2, primero debemos calcular $f(x_0, y_0)$, $f_x(x_0, y_0)$ y $f_y(x_0, y_0)$ usando $x_0 = 2$ y $y_0 = 3$:

$$ \begin{aligned} f(x_0, y_0) &= f(2, 3) = \sqrt{41 – 4(2)^2 – (3)^2} = \sqrt{41 – 16 – 9} = \sqrt{16} = 4 \\ f_x(x, y) &= -\frac{4x}{\sqrt{41 – 4x^2 – y^2}} \text{ por lo que } f_x(x_0, y_0) = -\frac{4(2)}{\sqrt{41 – 4(2)^2 – (3)^2}} = -2 \\ f_y(x, y) &= -\frac{y}{\sqrt{41 – 4x^2 – y^2}} \text{ por lo que } f_y(x_0, y_0) = -\frac{3}{\sqrt{41 – 4(2)^2 – (3)^2}} = -\frac{3}{4}. \end{aligned} $$

Ahora sustituimos estos valores en la Ecuación 11.4.2:

$$ \begin{aligned} L(x, y) &= f(x_0, y_0) + f_x(x_0, y_0)(x – x_0) + f_y(x_0, y_0)(y – y_0) \\ &= 4 – 2(x – 2) – \frac{3}{4}(y – 3) \\ &= \frac{41}{4} – 2x – \frac{3}{4}y. \end{aligned} $$

Por último, sustituimos $x = 2.1$ y $y = 2.9$ en $L(x, y)$:

$$L(2.1, 2.9) = \frac{41}{4} – 2(2.1) – \frac{3}{4}(2.9) = 10.25 – 4.2 – 2.175 = 3.875.$$

El valor aproximado de $f(2.1, 2.9)$ con cuatro decimales es

$$f(2.1, 2.9) = \sqrt{41 – 4(2.1)^2 – (2.9)^2} = \sqrt{14.95} \approx 3.8665,$$

lo cual corresponde a un error de aproximación del 0.2%. ♦

Ejercicio de control 11.4.2

Dada la función $f(x, y) = e^{5-2x+3y}$, aproxime $f(4.1, 0.9)$ utilizando el punto $(4, 1)$ para $(x_0, y_0)$. ¿Cuál es el valor aproximado de $f(4.1, 0.9)$ con cuatro decimales? ♦

Diferenciabilidad

Cuando se trabaja con una función $y = f(x)$ de una variable, se dice que la función es diferenciable en un punto $x = a$ si existe $f'(a)$. Además, si una función de una variable es diferenciable en un punto, la gráfica es “suave” en ese punto (es decir, no existen esquinas) y una recta tangente está bien definida en ese punto.

La idea detrás de la diferenciabilidad de una función de dos variables está conectada con la idea de suavidad en ese punto. En este caso, una superficie se considera suave en el punto $P$ si existe un plano tangente a la superficie en ese punto. Si una función es diferenciable en un punto, entonces existe un plano tangente a la superficie en ese punto. Recuerde que la fórmula para un plano tangente en un punto $(x_0, y_0)$ viene dada por

$$z = f(x_0, y_0) + f_x(x_0, y_0)(x – x_0) + f_y(x_0, y_0)(y – y_0),$$

Para que exista un plano tangente en el punto $(x_0, y_0)$, las derivadas parciales deben, por lo tanto, existir en ese punto. Sin embargo, esta no es una condición suficiente para la suavidad, como se ilustró en la Figura 11.4.3 . En ese caso, las derivadas parciales existían en el origen, pero la función también tenía una esquina en la gráfica en el origen.

Definición

Una función $f(x, y)$ es diferenciable en un punto $P(x_0, y_0)$ si, para todos los puntos $(x, y)$ en un disco $\delta$ alrededor de $P$, podemos escribir

$$f(x, y) = f(x_0, y_0) + f_x(x_0, y_0)(x – x_0) + f_y(x_0, y_0)(y – y_0) + E(x, y), \hspace{20pt} \text{(11.4.3)} $$

donde el término de error $E$ satisface

$$\lim_{(x,y) \to (x_0,y_0)} \frac{E(x, y)}{\sqrt{(x – x_0)^2 + (y – y_0)^2}} = 0.$$

♦

El último término en la Ecuación 11.4.3 se denomina término de error y representa qué tan cerca se encuentra el plano tangente de la superficie en un entorno pequeño (disco $\delta$) del punto $P$. Para que la función $f$ sea diferenciable en $P$, la función debe ser suave; es decir, la gráfica de $f$ debe estar cerca del plano tangente para puntos cercanos a $P$.

Ejemplo ilustrativo 11.4.4. Demostración de la diferenciabilidad

Demuestre que la función $f(x, y) = 2x^2 – 4y$ es diferenciable en el punto $(2, -3)$.

Solución:

Primero, calculamos $f(x_0, y_0)$, $f_x(x_0, y_0)$ y $f_y(x_0, y_0)$ usando $x_0 = 2$ y $y_0 = -3$, luego utilizamos la Ecuación 11.4.3 :

$$ \begin{aligned} f(2, -3) &= 2(2)^2 – 4(-3) = 8 + 12 = 20 \\ f_x(2, -3) &= 4(2) = 8 \\ f_y(2, -3) &= -4. \end{aligned} $$

Por lo tanto, $m_1 = 8$ y $m_2 = -4$, y la Ecuación 11.4.3 se convierte en:

$$ \begin{aligned} f(x, y) &= f(2, -3) + f_x(2, -3)(x – 2) + f_y(2, -3)(y + 3) + E(x, y) \\ 2x^2 – 4y &= 20 + 8(x – 2) – 4(y + 3) + E(x, y) \\ 2x^2 – 4y &= 20 + 8x – 16 – 4y – 12 + E(x, y) \\ 2x^2 – 4y &= 8x – 4y – 8 + E(x, y) \\ E(x, y) &= 2x^2 – 8x + 8. \end{aligned} $$

A continuación, calculamos $\lim_{(x,y) \to (x_0,y_0)} \frac{E(x, y)}{\sqrt{(x – x_0)^2 + (y – y_0)^2}}$:

$$ \begin{aligned} \lim_{(x,y) \to (2,-3)} \frac{E(x, y)}{\sqrt{(x – 2)^2 + (y + 3)^2}} &= \lim_{(x,y) \to (2,-3)} \frac{2x^2 – 8x + 8}{\sqrt{(x – 2)^2 + (y + 3)^2}} \\ &= \lim_{(x,y) \to (2,-3)} \frac{2(x^2 – 4x + 4)}{\sqrt{(x – 2)^2 + (y + 3)^2}} \\ &= \lim_{(x,y) \to (2,-3)} \frac{2(x – 2)^2}{\sqrt{(x – 2)^2 + (y + 3)^2}} \\ &\leq \lim_{(x,y) \to (2,-3)} \frac{2((x – 2)^2 + (y + 3)^2)}{\sqrt{(x – 2)^2 + (y + 3)^2}} \\ &= \lim_{(x,y) \to (2,-3)} 2\sqrt{(x – 2)^2 + (y + 3)^2} \\ &= 0. \end{aligned} $$

Dado que $E(x, y) \geq 0$ para cualquier valor de $x$ o $y$, el límite original debe ser igual a cero. Por lo tanto, $f(x, y) = 2x^2 – 4y$ es diferenciable en el punto $(2, -3)$. ♦

Ejercicio de control 11.4.3

Demuestre que la función $f(x, y) = 3x – 4y^2$ es diferenciable en el punto $(-1, 2)$. ♦

La función $f(x, y) = \begin{cases} \frac{xy}{\sqrt{x^2+y^2}} & (x,y) \neq (0,0) \\ 0 & (x,y) = (0,0) \end{cases}$ no es diferenciable en el origen. Podemos ver esto calculando las derivadas parciales. Esta función apareció anteriormente en la sección, donde demostramos que $f_x(0, 0) = f_y(0, 0) = 0$. Sustituyendo esta información en la Ecuación 11.4.3 usando $x_0 = 0$ y $y_0 = 0$, obtenemos:

$$ \begin{aligned} f(x, y) &= f(0, 0) + f_x(0, 0)(x – 0) + f_y(0, 0)(y – 0) + E(x, y) \\ E(x, y) &= \frac{xy}{\sqrt{x^2+y^2}}. \end{aligned} $$

Calcular $\lim_{(x,y) \to (x_0,y_0)} \frac{E(x, y)}{\sqrt{(x – x_0)^2 + (y – y_0)^2}}$ resulta en:

$$ \begin{aligned} \lim_{(x,y) \to (x_0,y_0)} \frac{E(x, y)}{\sqrt{(x – x_0)^2 + (y – y_0)^2}} &= \lim_{(x,y) \to (0,0)} \frac{\frac{xy}{\sqrt{x^2+y^2}}}{\sqrt{x^2+y^2}} \\ &= \lim_{(x,y) \to (0,0)} \frac{xy}{x^2+y^2}. \end{aligned} $$

Dependiendo de la trayectoria tomada hacia el origen, este límite toma diferentes valores. Por lo tanto, el límite no existe y la función $f$ no es diferenciable en el origen, como se muestra en la siguiente figura.

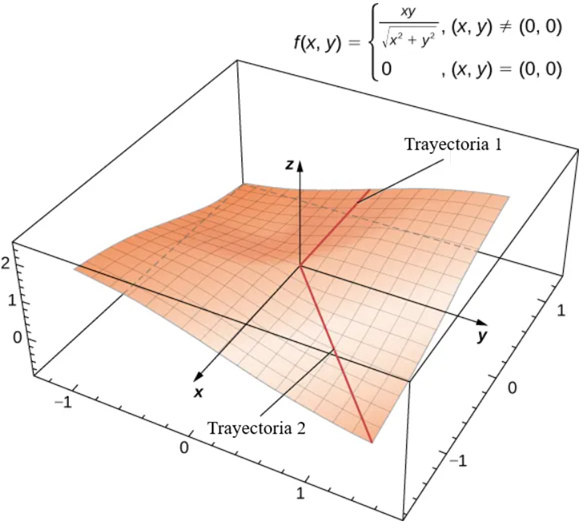
Figura 11.4.6 Esta función f (x, y) no es diferenciable en el origen.

La diferenciabilidad y la continuidad para funciones de dos o más variables están relacionadas, al igual que ocurre con las funciones de una sola variable. De hecho, con algunos ajustes en la notación, el teorema básico es el mismo.

Teorema 11.4.1. La diferenciabilidad implica continuidad

Sea $z = f(x, y)$ una función de dos variables con $(x_0, y_0)$ en el dominio de $f$. Si $f(x, y)$ es diferenciable en $(x_0, y_0)$, entonces $f(x, y)$ es continua en $(x_0, y_0)$. ♦

La Diferenciabilidad Implica Continuidad muestra que si una función es diferenciable en un punto, entonces es continua en dicho punto. Sin embargo, si una función es continua en un punto, no es necesariamente diferenciable en ese punto. Por ejemplo,

$$f(x, y) = \begin{cases} \frac{xy}{\sqrt{x^2+y^2}} & (x,y) \neq (0,0) \\ 0 & (x,y) = (0,0) \end{cases}$$

es continua en el origen, pero no es diferenciable en el origen. Esta observación también es similar a la situación en el cálculo de una sola variable.

La Continuidad de las Primeras Derivadas Parciales Implica Diferenciabilidad explora más a fondo la conexión entre la continuidad y la diferenciabilidad en un punto. Este teorema establece que si la función y sus derivadas parciales son continuas en un punto, la función es diferenciable.

Teorema 11.4.2. La continuidad de las derivadas parciales de primer orden implica diferenciabilidad

Sea $z = f(x, y)$ una función de dos variables con $(x_0, y_0)$ en el dominio de $f$. Si $f(x, y)$, $f_x(x, y)$, y $f_y(x, y)$ existen en un entorno de $(x_0, y_0)$ y son continuas en $(x_0, y_0)$, entonces $f(x, y)$ es diferenciable allí. ♦

Recuerde que anteriormente mostramos que la función

$$f(x, y) = \begin{cases} \frac{xy}{\sqrt{x^2+y^2}} & (x,y) \neq (0,0) \\ 0 & (x,y) = (0,0) \end{cases}$$

no era diferenciable en el origen. Calculemos las derivadas parciales $f_x$ y $f_y$:

$$\frac{\partial f}{\partial x} = \frac{y^3}{(x^2 + y^2)^{3/2}} \quad \text{and} \quad \frac{\partial f}{\partial y} = \frac{x^3}{(x^2 + y^2)^{3/2}}.$$

La contrarrecíproca del teorema anterior establece que si una función no es diferenciable, entonces al menos una de las hipótesis debe ser falsa. Exploremos la condición de que $f_x(0,0)$ debe ser continua. Para que esto sea cierto, debe cumplirse que $\lim_{(x,y) \to (0,0)} f_x(x,y) = f_x(0,0)$:

$$\lim_{(x,y) \to (0,0)} f_x(x, y) = \lim_{(x,y) \to (0,0)} \frac{y^3}{(x^2 + y^2)^{3/2}}.$$

Sea $x = ky$. Entonces:

$$ \begin{aligned} \lim_{(x,y) \to (0,0)} \frac{y^3}{(x^2 + y^2)^{3/2}} &= \lim_{y \to 0} \frac{y^3}{((ky)^2 + y^2)^{3/2}} \\ &= \lim_{y \to 0} \frac{y^3}{(k^2 y^2 + y^2)^{3/2}} \\ &= \lim_{y \to 0} \frac{y^3}{|y|^3 (k^2 + 1)^{3/2}} \\ &= \frac{1}{(k^2 + 1)^{3/2}} \lim_{y \to 0} \frac{|y|}{y}. \end{aligned} $$

Si $y > 0$, entonces esta expresión es igual a $1/(k^2 + 1)^{3/2}$; si $y < 0$, entonces es igual a $-(1/(k^2 + 1)^{3/2})$. En cualquier caso, el valor depende de $k$, por lo tanto, el límite no existe.

Diferenciales

En Aproximaciones Lineales y Diferenciales estudiamos primero el concepto de diferenciales. El diferencial de $y$, escrito como $dy$, se define como $f'(x) \, dx$. El diferencial se utiliza para aproximar $\Delta y = f(x + \Delta x) – f(x)$, donde $\Delta x = dx$. Al extender esta idea a la aproximación lineal de una función de dos variables en el punto $(x_0, y_0)$, se obtiene la fórmula para el diferencial total de una función de dos variables.

Definición

Sea $z = f(x, y)$ una función de dos variables con $(x_0, y_0)$ en el dominio de $f$, y sean $\Delta x$ y $\Delta y$ elegidos de tal manera que $(x_0 + \Delta x, y_0 + \Delta y)$ también esté en el dominio de $f$. Si $f$ es diferenciable en el punto $(x_0, y_0)$, entonces los diferenciales $dx$ y $dy$ se definen como

$$dx = \Delta x \quad \text{y} \quad dy = \Delta y.$$

El diferencial $dz$, también llamado el diferencial total de $z = f(x, y)$ en $(x_0, y_0)$, se define como

$$dz = f_x(x_0, y_0) \, dx + f_y(x_0, y_0) \, dy. \hspace{20pt} \text{(11.4.4)}$$

Observe que el símbolo $\partial$ no se utiliza para denotar el diferencial total; en su lugar, aparece $d$ delante de $z$. Ahora, definamos $\Delta z = f(x + \Delta x, y + \Delta y) – f(x, y)$. Usamos $dz$ para aproximar $\Delta z$, por lo que

$$\Delta z \approx dz = f_x(x_0, y_0) \, dx + f_y(x_0, y_0) \, dy.$$

Por lo tanto, el diferencial se utiliza para aproximar el cambio en la función $z = f(x_0, y_0)$ en el punto $(x_0, y_0)$ para valores dados de $\Delta x$ y $\Delta y$. Dado que $\Delta z = f(x + \Delta x, y + \Delta y) – f(x, y)$, esto puede utilizarse además para aproximar $f(x + \Delta x, y + \Delta y)$:

$$ \begin{aligned} f(x + \Delta x, y + \Delta y) &= f(x, y) + \Delta z \\ &\approx f(x, y) + f_x(x_0, y_0) \, \Delta x + f_y(x_0, y_0) \, \Delta y. \end{aligned} $$

Consulte la siguiente figura.

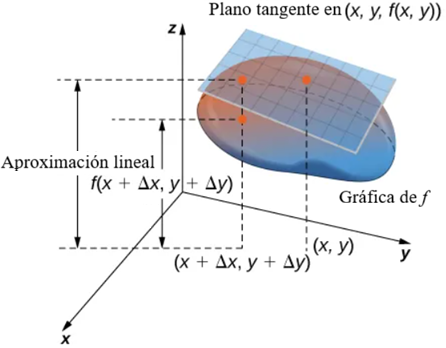
Figura 11.4.7 La aproximación lineal se calcula mediante la fórmula

$$ f(x + \Delta x, y + \Delta y) \approx f(x, y) + f_x(x_0, y_0)\,\Delta x + f_y(x_0, y_0)\,\Delta y. $$

Una aplicación de esta idea es determinar la propagación del error. Por ejemplo, si estamos fabricando un dispositivo y cometemos cierto error al medir una magnitud dada, el diferencial puede utilizarse para estimar el error en el volumen total del dispositivo.

Ejemplo ilustrativo 11.4.5. Aproximación mediante diferenciales

Encuentre el diferencial $dz$ de la función $f(x, y) = 3x^2 – 2xy + y^2$ y utilícelo para aproximar $\Delta z$ en el punto $(2, -3)$. Use $\Delta x = 0.1$ y $\Delta y = -0.05$. ¿Cuál es el valor exacto de $\Delta z$?

Solución:

Primero, debemos calcular $f(x_0, y_0)$, $f_x(x_0, y_0)$ y $f_y(x_0, y_0)$ usando $x_0 = 2$ y $y_0 = -3$:

$$ \begin{aligned} f(x_0, y_0) &= f(2, -3) = 3(2)^2 – 2(2)(-3) + (-3)^2 = 12 + 12 + 9 = 33 \\ f_x(x, y) &= 6x – 2y \\ f_y(x, y) &= -2x + 2y \\ f_x(x_0, y_0) &= f_x(2, -3) = 6(2) – 2(-3) = 12 + 6 = 18 \\ f_y(x_0, y_0) &= f_y(2, -3) = -2(2) + 2(-3) = -4 – 6 = -10. \end{aligned} $$

Luego, sustituimos estas cantidades en la Ecuación 11.4.4 :

$$ \begin{aligned} dz &= f_x(x_0, y_0) \, dx + f_y(x_0, y_0) \, dy \\ dz &= 18(0.1) – 10(-0.05) = 1.8 + 0.5 = 2.3. \end{aligned} $$

Esta es la aproximación a $\Delta z = f(x_0 + \Delta x, y_0 + \Delta y) – f(x_0, y_0)$. El valor exacto de $\Delta z$ viene dado por:

$$ \begin{aligned} \Delta z &= f(x_0 + \Delta x, y_0 + \Delta y) – f(x_0, y_0) \\ &= f(2 + 0.1, -3 – 0.05) – f(2, -3) \\ &= f(2.1, -3.05) – f(2, -3) \\ &= 2.3425. \end{aligned} $$

♦

Ejercicio de control 11.4.4

Encuentre el diferencial $dz$ de la función $f(x, y) = 4y^2 + x^2y – 2xy$ y utilícelo para aproximar $\Delta z$ en el punto $(1, -1)$. Use $\Delta x = 0.03$ y $\Delta y = -0.02$. ¿Cuál es el valor exacto de $\Delta z$? ♦

Diferenciabilidad de una función de tres variables

Todos los resultados anteriores sobre la diferenciabilidad de funciones de dos variables pueden generalizarse a funciones de tres variables. En primer lugar, la definición:

Definición

Una función $f(x, y, z)$ es diferenciable en un punto $P(x_0, y_0, z_0)$ si para todos los puntos $(x, y, z)$ en un disco $\delta$ alrededor de $P$ podemos escribir

$$ \begin{aligned} f(x, y, z) &= f(x_0, y_0, z_0) + f_x(x_0, y_0, z_0)(x – x_0) + f_y(x_0, y_0, z_0)(y – y_0) \\ &\quad + f_z(x_0, y_0, z_0)(z – z_0) + E(x, y, z), \end{aligned} $$

donde el término de error $E$ satisface

$$\lim_{(x,y,z) \to (x_0,y_0,z_0)} \frac{E(x, y, z)}{\sqrt{(x – x_0)^2 + (y – y_0)^2 + (z – z_0)^2}} = 0.$$

♦

Si una función de tres variables es diferenciable en un punto $(x_0, y_0, z_0)$, entonces es continua allí. Además, la continuidad de las primeras derivadas parciales en ese punto garantiza la diferenciabilidad.

Páginas: 1 2