| 11. Diferenciación de funciones de varias variables | Ejercicios propuestos para el Capítulo 11.3 |

11.3 Derivadas parciales

Objetivos de aprendizaje

Ahora que hemos examinado los límites y la continuidad de funciones de dos variables, podemos proceder al estudio de las derivadas. El cálculo de derivadas de funciones de dos variables es el concepto clave de este capítulo, con tantas aplicaciones en matemáticas, ciencia e ingeniería como la diferenciación de funciones de una sola variable. Sin embargo, ya hemos visto que los límites y la continuidad de funciones multivariables presentan nuevos problemas y requieren nueva terminología e ideas para abordarlos. Esto también se extiende al proceso de diferenciación.

Derivadas de una función de dos variables

Al estudiar derivadas de funciones de una variable, descubrimos que una interpretación de la derivada es una tasa de cambio instantánea de $y$ como una función de $x$. La notación de Leibniz para la derivada es $dy/dx$, lo cual implica que $y$ es la variable dependiente y $x$ es la variable independiente. Para una función $z = f(x, y)$ de dos variables, $x$ e $y$ son las variables independientes y $z$ es la variable dependiente. Esto plantea dos preguntas de inmediato: ¿Cómo adaptamos la notación de Leibniz para funciones de dos variables? Además, ¿cuál es una interpretación de la derivada? La respuesta reside en las derivadas parciales.

Definición

Sea $f(x, y)$ una función de dos variables. Entonces, la derivada parcial de $f$ con respecto a $x$, escrita como $\partial f / \partial x$ o $f_x$, se define como

$$ \frac{\partial f}{\partial x} = \lim_{h \to 0} \frac{f(x + h, y) – f(x, y)}{h}. \hspace{20pt} \text{(11.3.1)} $$

La derivada parcial de $f$ con respecto a $y$, escrita como $\partial f / \partial y$ o $f_y$, se define como

$$ \frac{\partial f}{\partial y} = \lim_{k \to 0} \frac{f(x, y + k) – f(x, y)}{k}. \hspace{20pt} \text{(11.3.2)}$$

♦

Esta definición ya muestra dos diferencias. Primero, la notación cambia, en el sentido de que todavía usamos una versión de la notación de Leibniz, pero la $d$ en la notación original se reemplaza con el símbolo $\partial$. (Esta “d” redondeada se suele llamar “parcial”, por lo que $\partial f / \partial x$ se lee como la “parcial de $f$ con respecto a $x$”). Este es el primer indicio de que estamos tratando con derivadas parciales. Segundo, ahora tenemos dos derivadas diferentes que podemos tomar, ya que hay dos variables independientes distintas. Dependiendo de qué variable elijamos, podemos obtener derivadas parciales totalmente diferentes, y a menudo lo hacemos.

Ejercicio ilustrativo 11.3.1. Cálculo de derivadas parciales a partir de la definición

Utilice la definición de la derivada parcial como un límite para calcular $\partial f / \partial x$ y $\partial f / \partial y$ para la función

$$ f(x, y) = x^2 – 3xy + 2y^2 – 4x + 5y – 12. $$

Solución:

Primero, calcule $f(x + h, y)$.

$$ \begin{aligned} f(x + h, y) &= (x + h)^2 – 3(x + h)y + 2y^2 – 4(x + h) + 5y – 12 \\ &= x^2 + 2xh + h^2 – 3xy – 3hy + 2y^2 – 4x – 4h + 5y – 12. \end{aligned} $$

A continuación, sustituya esto en la Definición (11.3.1). y simplifique:

$$ \begin{aligned} \frac{\partial f}{\partial x} &= \lim_{h \to 0} \frac{f(x+h, y) – f(x, y)}{h} \\ &= \lim_{h \to 0} \frac{(x^2 + 2xh + h^2 – 3xy – 3hy + 2y^2 – 4x – 4h + 5y – 12) – (x^2 – 3xy + 2y^2 – 4x + 5y – 12)}{h} \\ &= \lim_{h \to 0} \frac{x^2 + 2xh + h^2 – 3xy – 3hy + 2y^2 – 4x – 4h + 5y – 12 – x^2 + 3xy – 2y^2 + 4x – 5y + 12}{h} \\ &= \lim_{h \to 0} \frac{2xh + h^2 – 3hy – 4h}{h} \\ &= \lim_{h \to 0} \frac{h(2x + h – 3y – 4)}{h} \\ &= \lim_{h \to 0} (2x + h – 3y – 4) \\ &= 2x – 3y – 4. \end{aligned} $$

Para calcular $\frac{\partial f}{\partial y}$, primero calcule $f(x, y + h)$:

$$ \begin{aligned} f(x, y + h) &= x^2 – 3x(y + h) + 2(y + h)^2 – 4x + 5(y + h) – 12 \\ &= x^2 – 3xy – 3xh + 2y^2 + 4yh + 2h^2 – 4x + 5y + 5h – 12. \end{aligned} $$

Luego, sustituya esto en la Definición (11.3.2). y simplifique:

$$ \begin{aligned} \frac{\partial f}{\partial y} &= \lim_{k \to 0} \frac{f(x, y+h) – f(x, y)}{k} \\ &= \lim_{k \to 0} \frac{(x^2 – 3xy – 3xk + 2y^2 + 4yk + 2k^2 – 4x + 5y + 5k – 12) – (x^2 – 3xy + 2y^2 – 4x + 5y – 12)}{k} \\ &= \lim_{k \to 0} \frac{x^2 – 3xy – 3xk + 2y^2 + 4yk + 2k^2 – 4x + 5y + 5k – 12 – x^2 + 3xy – 2y^2 + 4x – 5y + 12}{k} \\ &= \lim_{k \to 0} \frac{-3xk + 4yk + 2k^2 + 5k}{k} \\ &= \lim_{k \to 0} \frac{k(-3x + 4y + 2k + 5)}{k} \\ &= \lim_{k \to 0} (-3x + 4y + 2k + 5) \\ &= -3x + 4y + 5. \end{aligned} $$

♦

Ejercicio de control 11.3.1

Use la definición de la derivada parcial como un límite para calcular $\partial f/\partial x$ y $\partial f/\partial y$ para la función

$$ f(x, y) = 4x^2 + 2xy – y^2 + 3x – 2y + 5. $$ ♦

La idea fundamental que se debe tener en cuenta al calcular derivadas parciales es tratar todas las variables independientes, excepto aquella con respecto a la cual estamos derivando, como constantes. Luego, se procede a derivar como se haría con una función de una sola variable.

Para ver por qué esto es cierto, primero fijamos $y$ y definimos $g(x) = f(x, y)$ como una función de $x$. Entonces:

$$ g'(x) = \lim_{h \to 0} \frac{g(x + h) – g(x)}{h} = \lim_{h \to 0} \frac{f(x + h, y) – f(x, y)}{h} = \frac{\partial f}{\partial x}. $$

Lo mismo ocurre al calcular la derivada parcial de $f$ con respecto a $y$. Esta vez, fijamos $x$ y definimos $h(y) = f(x, y)$ como una función de $y$. Entonces:

$$ h'(y) = \lim_{k \to 0} \frac{h(y + k) – h(y)}{k} = \lim_{k \to 0} \frac{f(x, y + k) – f(x, y)}{k} = \frac{\partial f}{\partial y}. $$

Todas las reglas de diferenciación de la Introducción a las derivadas son aplicables.

Ejercicio ilustrativo 11.3.2. Cálculo de derivadas parciales

Calcule $\partial f / \partial x$ y $\partial f / \partial y$ para las siguientes funciones manteniendo la variable opuesta constante y luego derivando:

1. $f(x, y) = x^2 – 3xy + 2y^2 – 4x + 5y – 12$
2. $g(x, y) = \sin(x^2 y – 2x + 4)$

Solución:

a. Para calcular $\partial f/\partial x$, trate la variable $y$ como una constante. Luego, diferencie $f(x, y)$ con respecto a $x$ usando las reglas de la suma, la diferencia y la potencia:

$$ \begin{aligned} \frac{\partial f}{\partial x} &= \frac{\partial}{\partial x} [x^2 – 3xy + 2y^2 – 4x + 5y – 12] \\ &= \frac{\partial}{\partial x} [x^2] – \frac{\partial}{\partial x} [3xy] + \frac{\partial}{\partial x} [2y^2] – \frac{\partial}{\partial x} [4x] + \frac{\partial}{\partial x} [5y] – \frac{\partial}{\partial x} [12] \\ &= 2x – 3y + 0 – 4 + 0 – 0 \\ &= 2x – 3y – 4. \end{aligned} $$

Las derivadas del tercer, quinto y sexto término son todas cero porque no contienen la variable $x$, por lo que se tratan como términos constantes. La derivada del segundo término es igual al coeficiente de $x$, que es $-3y$. Calculando $\partial f/\partial y$:

$$ \begin{aligned} \frac{\partial f}{\partial y} &= \frac{\partial}{\partial y} [x^2 – 3xy + 2y^2 – 4x + 5y – 12] \\ &= \frac{\partial}{\partial y} [x^2] – \frac{\partial}{\partial y} [3xy] + \frac{\partial}{\partial y} [2y^2] – \frac{\partial}{\partial y} [4x] + \frac{\partial}{\partial y} [5y] – \frac{\partial}{\partial y} [12] \\ &= 0 – 3x + 4y – 0 + 5 – 0 \\ &= -3x + 4y + 5. \end{aligned} $$

Estos son los mismos resultados obtenidos en el Ejemplo ilustrativo 11.3.1.

b. Para calcular $\partial g/\partial x$, trate la variable $y$ como una constante. Luego, diferencie $g(x, y)$ con respecto a $x$ usando la regla de la cadena y la regla de la potencia:

$$ \begin{aligned} \frac{\partial g}{\partial x} &= \frac{\partial}{\partial x} [\sin(x^2y – 2x + 4)] \\ &= \cos(x^2y – 2x + 4) \frac{\partial}{\partial x} [x^2y – 2x + 4] \\ &= (2xy – 2) \cos(x^2y – 2x + 4). \end{aligned} $$

Para calcular $\partial g/\partial y$, trate la variable $x$ como una constante. Luego, diferencie $g(x, y)$ con respecto a $y$ usando la regla de la cadena y la regla de la potencia:

$$ \begin{aligned} \frac{\partial g}{\partial y} &= \frac{\partial}{\partial y} [\sin(x^2y – 2x + 4)] \\ &= \cos(x^2y – 2x + 4) \frac{\partial}{\partial y} [x^2y – 2x + 4] \\ &= x^2 \cos(x^2y – 2x + 4). \end{aligned} $$

♦

Ejercicio de control 11.3.2

Calcule $\partial f / \partial x$ y $\partial f / \partial y$ para la función $f(x, y) = \tan(x^3 – 3x^2y^2 + 2y^4)$ manteniendo la variable opuesta constante y luego derivando. ♦

¿Cómo podemos interpretar estas derivadas parciales? Recuerda que la gráfica de una función de dos variables es una superficie en $\mathbb{R}^3$. Si eliminamos el límite de la definición de la derivada parcial con respecto a $x$, queda el cociente de diferencias:

$$ \frac{f(x + h, y) – f(x, y)}{h}. $$

Esto se asemeja al cociente de diferencias para la derivada de una función de una variable, excepto por la presencia de la variable $y$. La Figura 11.3.1 ilustra una superficie descrita por una función arbitraria $z = f(x, y)$.

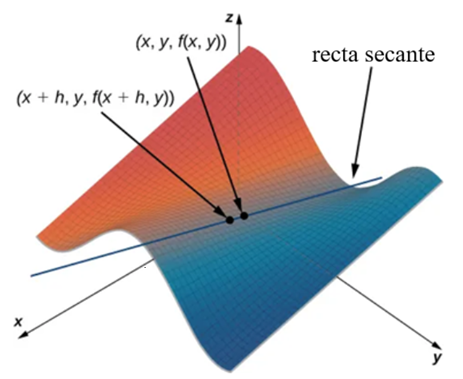
En la Figura 9.3.1, el valor de $h$ es positivo. Si graficamos $f(x, y)$ y $f(x + h, y)$ para un punto arbitrario $(x, y)$, entonces la pendiente de la recta secante que pasa por estos dos puntos está dada por

$$ \frac{f(x + h, y) – f(x, y)}{h}. $$

Esta línea es paralela al plano $x-z$. Por lo tanto, la pendiente de la recta secante representa una tasa de cambio promedio de la función $f$ a medida que nos desplazamos paralelamente al eje $x$. A medida que $h$ se aproxima a cero, la pendiente de la recta secante se aproxima a la pendiente de la recta tangente.

Si decidimos cambiar $y$ en lugar de $x$ por el mismo valor incremental $h$, entonces la recta secante es paralela al eje $y$ y también lo es la recta tangente. Por lo tanto, $\partial f / \partial x$ representa la pendiente de la recta tangente que pasa por el punto $(x, y, f(x, y))$ paralela al eje $x$ y $\partial f / \partial y$ representa la pendiente de la recta tangente que pasa por el punto $(x, y, f(x, y))$ paralela al eje $y$. Si deseamos encontrar la pendiente de una recta tangente que pase por el mismo punto en cualquier otra dirección, entonces necesitamos lo que se denominan derivadas direccionales, las cuales discutiremos en Derivadas Direccionales y el Gradiente.

Ahora volvemos a la idea de los mapas de contorno, que introdujimos en Funciones de varias variables. Podemos usar un mapa de contorno para estimar las derivadas parciales de una función $g(x, y)$.

Ejercicio ilustrativo 11.3.3. Derivadas parciales a partir de un mapa de contornos

Use un mapa de contorno para estimar $\partial g / \partial x$ en el punto $(\sqrt{5}, 0)$ para la función $g(x, y) = \sqrt{9 – x^2 – y^2}$.

Solución:

El siguiente gráfico representa un mapa de contorno para la función $g(x, y) = \sqrt{9 – x^2 – y^2}$.

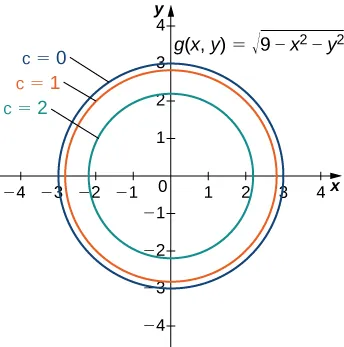
Figura 11.3.2 Mapa de contorno para la función $g(x,y) = \sqrt{9 – x^2 – y^2}$, usando $c = 0, 1, 2,$ y $3$ ($c = 3$ corresponde al origen).

El círculo interior en el mapa de contorno corresponde a $c = 2$ y el siguiente círculo hacia afuera corresponde a $c = 1$. El primer círculo viene dado por la ecuación $2 = \sqrt{9 – x^2 – y^2}$; el segundo círculo viene dado por la ecuación $1 = \sqrt{9 – x^2 – y^2}$. La primera ecuación se simplifica a $x^2 + y^2 = 5$ y la segunda ecuación se simplifica a $x^2 + y^2 = 8$. La intersección con el eje $x$ del primer círculo es $(\sqrt{5}, 0)$ y la intersección con el eje $x$ del segundo círculo es $(2\sqrt{2}, 0)$. Podemos estimar el valor de $\partial g/\partial x$ evaluado en el punto $(\sqrt{5}, 0)$ usando la fórmula de la pendiente:

$$ \left.\frac{\partial g}{\partial x}\right|_{(x,y)=(\sqrt{5},0)} \approx \frac{g(\sqrt{5}, 0) – g(2\sqrt{2}, 0)}{\sqrt{5} – 2\sqrt{2}} = \frac{2 – 1}{\sqrt{5} – 2\sqrt{2}} = \frac{1}{\sqrt{5} – 2\sqrt{2}} \approx -1.688. $$

Para calcular el valor exacto de $\partial g/\partial x$ evaluado en el punto $(\sqrt{5}, 0)$, comenzamos encontrando $\partial g/\partial x$ usando la regla de la cadena. Primero, reescribimos la función como $g(x, y) = \sqrt{9 – x^2 – y^2} = (9 – x^2 – y^2)^{1/2}$ y luego derivamos con respecto a $x$ mientras mantenemos $y$ constante:

$$ \frac{\partial g}{\partial x} = \frac{1}{2}(9 – x^2 – y^2)^{-1/2}(-2x) = -\frac{x}{\sqrt{9 – x^2 – y^2}}. $$

A continuación, evaluamos esta expresión usando $x = \sqrt{5}$ e $y = 0$:

$$ \left.\frac{\partial g}{\partial x}\right|_{(x,y)=(\sqrt{5},0)} = -\frac{\sqrt{5}}{\sqrt{9 – (\sqrt{5})^2 – (0)^2}} = -\frac{\sqrt{5}}{\sqrt{4}} = -\frac{\sqrt{5}}{2} \approx -1.118. $$

La estimación de la derivada parcial corresponde a la pendiente de la recta secante que pasa por los puntos $(\sqrt{5}, 0, g(\sqrt{5}, 0))$ y $(2\sqrt{2}, 0, g(2\sqrt{2}, 0))$. Representa una aproximación a la pendiente de la recta tangente a la superficie a través del punto $(\sqrt{5}, 0, g(\sqrt{5}, 0))$, la cual es paralela al eje $x$. ♦

Ejercicio de control 11.3.3

Use un mapa de contorno para estimar $\partial f / \partial y$ en el punto $(0, \sqrt{2})$ para la función

$$ f(x, y) = x^2 – y^2. $$

Compare esto con la respuesta exacta. ♦

Funciones de más de dos variables

Supongamos que tenemos una función de tres variables, como w = f (x, y, z). Podemos calcular derivadas parciales de w con respecto a cualquiera de las variables independientes, simplemente como extensiones de las definiciones de las derivadas parciales de funciones de dos variables.

Definición

Sea $f(x, y, z)$ una función de tres variables. Entonces, la derivada parcial de $f$ con respecto a $x$, escrita como $\partial f / \partial x$ o $f_x$, se define como

$$ \frac{\partial f}{\partial x} = \lim_{h \to 0} \frac{f(x + h, y, z) – f(x, y, z)}{h}. \hspace{20pt} \text{(11.3.3)} $$

La derivada parcial de $f$ con respecto a $y$, escrita como $\partial f / \partial y$ o $f_y$, se define como

$$ \frac{\partial f}{\partial y} = \lim_{k \to 0} \frac{f(x, y + k, z) – f(x, y, z)}{k}. \hspace{20pt} \text{(11.3.4)} $$

La derivada parcial de $f$ con respecto a $z$, escrita como $\partial f / \partial z$ o $f_z$, se define como

$$ \frac{\partial f}{\partial z} = \lim_{m \to 0} \frac{f(x, y, z + m) – f(x, y, z)}{m}. \hspace{20pt} \text{(11.3.5)} $$

♦

Podemos calcular la derivada parcial de una función de tres variables utilizando la misma idea que empleamos para una función de dos variables. Por ejemplo, si tenemos una función $f$ de $x$, $y$ y $z$, y deseamos calcular $\partial f/\partial x$, tratamos las otras dos variables independientes como si fueran constantes y luego derivamos con respecto a $x$.

Ejercicio ilustrativo 11.3.4. Cálculo de derivadas parciales para una función de tres variables

Use la definición de límite de las derivadas parciales para calcular $\partial f / \partial x$ para la función

$$ f(x, y, z) = x^2 – 3xy + 2y^2 – 4xz + 5yz^2 – 12x + 4y – 3z. $$

Luego, encuentre $\partial f / \partial y$ y $\partial f / \partial z$ estableciendo las otras dos variables como constantes y derivando en consecuencia.

Solución:

Primero calculamos $\partial f/\partial x$ usando la Ecuación 11.3.3, luego calculamos las otras dos derivadas parciales manteniendo constantes las variables restantes. Para usar la ecuación para encontrar $\partial f/\partial x$, primero necesitamos calcular $f(x + h, y, z)$:

$$ \begin{aligned} f(x + h, y, z) &= (x + h)^2 – 3(x + h)y + 2y^2 – 4(x + h)z + 5yz^2 – 12(x + h) + 4y – 3z \\ &= x^2 + 2xh + h^2 – 3xy – 3xh + 2y^2 – 4xz – 4hz + 5yz^2 – 12x – 12h + 4y – 3z \end{aligned} $$

y recordamos que $f(x, y, z) = x^2 – 3xy + 2y^2 – 4xz + 5yz^2 – 12x + 4y – 3z$. A continuación, sustituimos estas dos expresiones en la ecuación:

$$ \begin{aligned} \frac{\partial f}{\partial x} &= \lim_{h \to 0} \left[ \frac{x^2 + 2xh + h^2 – 3xy – 3xh + 2y^2 – 4xz – 4hz + 5yz^2 – 12x – 12h + 4y – 3z}{h} \right. \\ &\quad \left. – \frac{x^2 – 3xy + 2y^2 – 4xz + 5yz^2 – 12x + 4y – 3z}{h} \right] \\ &= \lim_{h \to 0} \left[ \frac{2xh + h^2 – 3hy – 4hz – 12h}{h} \right] \\ &= \lim_{h \to 0} \left[ \frac{h(2x + h – 3y – 4z – 12)}{h} \right] \\ &= \lim_{h \to 0} (2x + h – 3y – 4z – 12) \\ &= 2x – 3y – 4z – 12. \end{aligned} $$

Luego encontramos $\partial f/\partial y$ manteniendo $x$ y $z$ constantes. Por lo tanto, cualquier término que no incluya la variable $y$ es constante y su derivada es cero. Podemos aplicar las reglas de la suma, la diferencia y la potencia para funciones de una variable:

$$ \begin{aligned} &\frac{\partial}{\partial y} [x^2 – 3xy + 2y^2 – 4xz + 5yz^2 – 12x + 4y – 3z] \\ &= \frac{\partial}{\partial y} [x^2] – \frac{\partial}{\partial y} [3xy] + \frac{\partial}{\partial y} [2y^2] – \frac{\partial}{\partial y} [4xz] + \frac{\partial}{\partial y} [5yz^2] – \frac{\partial}{\partial y} [12x] + \frac{\partial}{\partial y} [4y] – \frac{\partial}{\partial y} [3z] \\ &= 0 – 3x + 4y – 0 + 5z^2 – 0 + 4 – 0 \\ &= -3x + 4y + 5z^2 + 4. \end{aligned} $$

Para calcular $\partial f/\partial z$, mantenemos $x$ e $y$ constantes y aplicamos las reglas de la suma, la diferencia y la potencia para funciones de una variable:

$$ \begin{aligned} &\frac{\partial}{\partial z} [x^2 – 3xy + 2y^2 – 4xz + 5yz^2 – 12x + 4y – 3z] \\ &= \frac{\partial}{\partial z} [x^2] – \frac{\partial}{\partial z} [3xy] + \frac{\partial}{\partial z} [2y^2] – \frac{\partial}{\partial z} [4xz] + \frac{\partial}{\partial z} [5yz^2] – \frac{\partial}{\partial z} [12x] + \frac{\partial}{\partial z} [4y] – \frac{\partial}{\partial z} [3z] \\ &= 0 – 0 + 0 – 4x + 10yz – 0 + 0 – 3 \\ &= -4x + 10yz – 3. \end{aligned} $$

♦

Ejercicio de control 11.3.4

Use la definición de límite de las derivadas parciales para calcular $\partial f/\partial x$ para la función

$$ f(x, y, z) = 2x^2 – 4x^2y + 2y^2 + 5xz^2 – 6x + 3z – 8. $$

Luego, encuentre $\partial f/\partial y$ y $\partial f/\partial z$ estableciendo las otras dos variables como constantes y derivando en consecuencia. ♦

Ejercicio ilustrativo 11.3.5. Cálculo de derivadas parciales para una función de tres variables

Calcule las tres derivadas parciales de las siguientes funciones:

1. $f(x, y, z) = \frac{x^2 y – 4xz + y^2}{x – 3yz}$
2. $g(x, y, z) = \sin(x^2 y – z) + \cos(x^2 – yz)$

Solución:

En cada caso, trate todas las variables como constantes excepto aquella cuya derivada parcial está calculando.

a.

$$ \begin{aligned} \frac{\partial f}{\partial x} &= \frac{\partial}{\partial x} \left[ \frac{x^2 y – 4xz + y^2}{x – 3yz} \right] \\ &= \frac{\frac{\partial}{\partial x}(x^2 y – 4xz + y^2)(x – 3yz) – (x^2 y – 4xz + y^2)\frac{\partial}{\partial x}(x – 3yz)}{(x – 3yz)^2} \\ &= \frac{(2xy – 4z)(x – 3yz) – (x^2 y – 4xz + y^2)(1)}{(x – 3yz)^2} \\ &= \frac{2x^2 y – 6xy^2 z – 4xz + 12yz^2 – x^2 y + 4xz – y^2}{(x – 3yz)^2} \\ &= \frac{x^2 y – 6xy^2 z + 12yz^2 – y^2}{(x – 3yz)^2} \end{aligned} $$ $$ \begin{aligned} \frac{\partial f}{\partial y} &= \frac{\partial}{\partial y} \left[ \frac{x^2 y – 4xz + y^2}{x – 3yz} \right] \\ &= \frac{\frac{\partial}{\partial y}(x^2 y – 4xz + y^2)(x – 3yz) – (x^2 y – 4xz + y^2)\frac{\partial}{\partial y}(x – 3yz)}{(x – 3yz)^2} \\ &= \frac{(x^2 + 2y)(x – 3yz) – (x^2 y – 4xz + y^2)(-3z)}{(x – 3yz)^2} \\ &= \frac{x^3 – 3x^2 yz + 2xy – 6y^2 z + 3x^2 yz – 12xz^2 + 3y^2 z}{(x – 3yz)^2} \\ &= \frac{x^3 + 2xy – 3y^2 z – 12xz^2}{(x – 3yz)^2} \end{aligned} $$ $$ \begin{aligned} \frac{\partial f}{\partial z} &= \frac{\partial}{\partial z} \left[ \frac{x^2 y – 4xz + y^2}{x – 3yz} \right] \\ &= \frac{\frac{\partial}{\partial z}(x^2 y – 4xz + y^2)(x – 3yz) – (x^2 y – 4xz + y^2)\frac{\partial}{\partial z}(x – 3yz)}{(x – 3yz)^2} \\ &= \frac{(-4x)(x – 3yz) – (x^2 y – 4xz + y^2)(-3y)}{(x – 3yz)^2} \\ &= \frac{-4x^2 + 12xyz + 3x^2 y^2 – 12xyz + 3y^3}{(x – 3yz)^2} \\ &= \frac{-4x^2 + 3x^2 y^2 + 3y^3}{(x – 3yz)^2} \end{aligned} $$

b.

$$ \begin{aligned} \frac{\partial g}{\partial x} &= \frac{\partial}{\partial x} [\sin(x^2 y – z) + \cos(x^2 – yz)] \\ &= (\cos(x^2 y – z)) \frac{\partial}{\partial x}(x^2 y – z) – (\sin(x^2 – yz)) \frac{\partial}{\partial x}(x^2 – yz) \\ &= 2xy \cos(x^2 y – z) – 2x \sin(x^2 – yz) \end{aligned} $$ $$ \begin{aligned} \frac{\partial g}{\partial y} &= \frac{\partial}{\partial y} [\sin(x^2 y – z) + \cos(x^2 – yz)] \\ &= (\cos(x^2 y – z)) \frac{\partial}{\partial y}(x^2 y – z) – (\sin(x^2 – yz)) \frac{\partial}{\partial y}(x^2 – yz) \\ &= x^2 \cos(x^2 y – z) + z \sin(x^2 – yz) \end{aligned} $$ $$ \begin{aligned} \frac{\partial g}{\partial z} &= \frac{\partial}{\partial z} [\sin(x^2 y – z) + \cos(x^2 – yz)] \\ &= (\cos(x^2 y – z)) \frac{\partial}{\partial z}(x^2 y – z) – (\sin(x^2 – yz)) \frac{\partial}{\partial z}(x^2 – yz) \\ &= -\cos(x^2 y – z) + y \sin(x^2 – yz) \end{aligned} $$

♦

Ejercicio de control 11.3.5

Calcule $\partial f / \partial x$, $\partial f / \partial y$ y $\partial f / \partial z$ para la función $f(x, y, z) = \sec(x^2 y) – \tan(x^3 y z^2)$.

♦

Derivadas parciales de orden superior

Considere la función

$$ f(x, y) = 2x^3 – 4xy^2 + 5y^3 – 6xy + 5x – 4y + 12. $$

Sus derivadas parciales son

$$ \frac{\partial f}{\partial x} = 6x^2 – 4y^2 – 6y + 5 \quad \text{y} \quad \frac{\partial f}{\partial y} = -8xy + 15y^2 – 6x – 4. $$

Cada una de estas derivadas parciales es una función de dos variables, por lo que podemos calcular las derivadas parciales de estas funciones. Al igual que con las derivadas de funciones de una sola variable, podemos llamarlas derivadas de segundo orden, derivadas de tercer orden, y así sucesivamente. En general, se denominan derivadas parciales de orden superior. Existen cuatro derivadas parciales de segundo orden para cualquier función (siempre que todas existan):

$$ \frac{\partial^2 f}{\partial x^2} = \frac{\partial}{\partial x} \left[ \frac{\partial f}{\partial x} \right], \quad \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial}{\partial x} \left[ \frac{\partial f}{\partial y} \right], \quad \frac{\partial^2 f}{\partial y \partial x} = \frac{\partial}{\partial y} \left[ \frac{\partial f}{\partial x} \right], \quad \frac{\partial^2 f}{\partial y^2} = \frac{\partial}{\partial y} \left[ \frac{\partial f}{\partial y} \right]. $$

Una notación alternativa para cada una es $f_{xx}, f_{yx}, f_{xy},$ y $f_{yy}$, respectivamente. Las derivadas parciales de orden superior calculadas con respecto a diferentes variables, como $f_{xy}$ y $f_{yx}$, se denominan comúnmente derivadas parciales mixtas.

Ejercicio ilustrativo 11.3.6. Cálculo de derivadas parciales de segundo orden

Calcule las cuatro segundas derivadas parciales para la función

$$ f(x, y) = xe^{-3y} + \sin(2x – 5y). $$

Solución:

Para calcular $\partial^2 f / \partial x^2$ y $\partial^2 f / \partial y \partial x$, primero calculamos $\partial f / \partial x$:

$$ \frac{\partial f}{\partial x} = e^{-3y} + 2 \cos(2x – 5y). $$

Para calcular $\partial^2 f / \partial x^2$, derivamos $\partial f / \partial x$ con respecto a $x$:

$$ \begin{aligned} \frac{\partial^2 f}{\partial x^2} &= \frac{\partial}{\partial x} \left[ \frac{\partial f}{\partial x} \right] \\ &= \frac{\partial}{\partial x} [e^{-3y} + 2 \cos(2x – 5y)] \\ &= -4 \sin(2x – 5y). \end{aligned} $$

Para calcular $\partial^2 f / \partial y \partial x$, derivamos $\partial f / \partial x$ con respecto a $y$:

$$ \begin{aligned} \frac{\partial^2 f}{\partial y \partial x} &= \frac{\partial}{\partial y} \left[ \frac{\partial f}{\partial x} \right] \\ &= \frac{\partial}{\partial y} [e^{-3y} + 2 \cos(2x – 5y)] \\ &= -3e^{-3y} + 10 \sin(2x – 5y). \end{aligned} $$

Para calcular $\partial^2 f / \partial x \partial y$ y $\partial^2 f / \partial y^2$, primero calculamos $\partial f / \partial y$:

$$ \frac{\partial f}{\partial y} = -3xe^{-3y} – 5 \cos(2x – 5y). $$

Para calcular $\partial^2 f / \partial x \partial y$, derivamos $\partial f / \partial y$ con respecto a $x$:

$$ \begin{aligned} \frac{\partial^2 f}{\partial x \partial y} &= \frac{\partial}{\partial x} \left[ \frac{\partial f}{\partial y} \right] \\ &= \frac{\partial}{\partial x} [-3xe^{-3y} – 5 \cos(2x – 5y)] \\ &= -3e^{-3y} + 10 \sin(2x – 5y). \end{aligned} $$

Para calcular $\partial^2 f / \partial y^2$, derivamos $\partial f / \partial y$ con respecto a $y$:

$$ \begin{aligned} \frac{\partial^2 f}{\partial y^2} &= \frac{\partial}{\partial y} \left[ \frac{\partial f}{\partial y} \right] \\ &= \frac{\partial}{\partial y} [-3xe^{-3y} – 5 \cos(2x – 5y)] \\ &= 9xe^{-3y} – 25 \sin(2x – 5y). \end{aligned} $$

♦

Ejercicio de control 11.3.6

Calcule las cuatro segundas derivadas parciales para la función

$$ f(x, y) = \sin(3x – 2y) + \cos(x + 4y). $$ ♦

Llegados a este punto, deberíamos notar que, tanto en el Ejemplo 11.3.6 como en el ejercicio de control, se cumplió que $\partial^2 f / \partial x \partial y = \partial^2 f / \partial y \partial x$. Bajo ciertas condiciones, esto siempre es cierto. De hecho, es una consecuencia directa del siguiente teorema.

Teorema 11.3.1. Igualdad de las derivadas parciales mixtas (teorema de Clairaut)

Suponga que $f(x, y)$ está definida en un disco abierto $D$ que contiene al punto $(a, b)$. Si las funciones $f_{xy}$ y $f_{yx}$ son continuas en $D$, entonces $f_{xy} = f_{yx}$. ♦

El teorema de Clairaut garantiza que, siempre que las derivadas parciales mixtas de segundo orden sean continuas, el orden en el que elijamos diferenciar las funciones (es decir, qué variable va primero, luego la segunda, y así sucesivamente) no importa. Este resultado también puede extenderse a derivadas de orden superior. La demostración del teorema de Clairaut puede encontrarse en la mayoría de los libros de cálculo avanzado.

Se pueden calcular otras dos derivadas parciales de segundo orden para cualquier función $f(x, y)$. La derivada parcial $f_{xx}$ es igual a la derivada parcial de $f_x$ con respecto a $x$, y $f_{yy}$ es igual a la derivada parcial de $f_y$ con respecto a $y$.

Ecuaciones diferenciales parciales

Una ecuación diferencial parcial es una ecuación que involucra una función desconocida de más de una variable independiente y una o más de sus derivadas parciales. Ejemplos de ecuaciones diferenciales parciales son:

$$ u_t = c^2 (u_{xx} + u_{yy}) \hspace{20pt} \text{(11.3.6)} $$

(ecuación de calor en dos dimensiones)

$$ u_{tt} = c^2 (u_{xx} + u_{yy}) \hspace{20pt} \text{(11.3.7)} $$

(ecuación de onda en dos dimensiones)

$$ u_{xx} + u_{yy} = 0 \hspace{20pt} \text{(11.3.8)} $$

(ecuación de Laplace en dos dimensiones)

En las dos primeras ecuaciones, la función desconocida $u$ tiene tres variables independientes — $t, x, y$ — y $c$ es una constante arbitraria. Las variables independientes $x$ e $y$ se consideran variables espaciales, y la variable $t$ representa el tiempo. En la ecuación de Laplace, la función desconocida $u$ tiene dos variables independientes $x$ e $y$.

Ejercicio ilustrativo 11.3.7. Una solución de la ecuación de onda

Verifique que

$$ u(x, y, t) = 5 \sin(3\pi x) \sin(4\pi y) \cos(10\pi t) $$

es una solución de la ecuación de onda

$$ u_{tt} = 4(u_{xx} + u_{yy}). \hspace{20pt} \text{(11.3.9)} $$

Solución:

Primero, calculamos $u_{tt}$, $u_{xx}$, y $u_{yy}$:

$$ \begin{aligned} u_{tt} &= \frac{\partial}{\partial t} \left[ \frac{\partial u}{\partial t} \right] \\ &= \frac{\partial}{\partial t} [5 \sin (3\pi x) \sin (4\pi y) (-10\pi \sin (10\pi t))] \\ &= \frac{\partial}{\partial t} [-50\pi \sin (3\pi x) \sin (4\pi y) \sin (10\pi t)] \\ &= -500\pi^2 \sin (3\pi x) \sin (4\pi y) \cos (10\pi t) \end{aligned} $$ $$ \begin{aligned} u_{xx} &= \frac{\partial}{\partial x} \left[ \frac{\partial u}{\partial x} \right] \\ &= \frac{\partial}{\partial x} [15\pi \cos (3\pi x) \sin (4\pi y) \cos (10\pi t)] \\ &= -45\pi^2 \sin (3\pi x) \sin (4\pi y) \cos (10\pi t) \end{aligned} $$ $$ \begin{aligned} u_{yy} &= \frac{\partial}{\partial y} \left[ \frac{\partial u}{\partial y} \right] \\ &= \frac{\partial}{\partial y} [5 \sin (3\pi x) (4\pi \cos (4\pi y)) \cos (10\pi t)] \\ &= \frac{\partial}{\partial y} [20\pi \sin (3\pi x) \cos (4\pi y) \cos (10\pi t)] \\ &= -80\pi^2 \sin (3\pi x) \sin (4\pi y) \cos (10\pi t). \end{aligned} $$

A continuación, sustituimos cada uno de estos términos en el lado derecho de la Ecuación 11.3.9 y simplificamos:

$$ \begin{aligned} 4(u_{xx} + u_{yy}) &= 4 (-45\pi^2 \sin (3\pi x) \sin (4\pi y) \cos (10\pi t) + (-80\pi^2 \sin (3\pi x) \sin (4\pi y) \cos (10\pi t)) \\ &= 4 (-125\pi^2 \sin (3\pi x) \sin (4\pi y) \cos (10\pi t)) \\ &= -500\pi^2 \sin (3\pi x) \sin (4\pi y) \cos (10\pi t) \\ &= u_{tt}. \end{aligned} $$

Esto verifica la solución. ♦

Ejercicio de control 11.3.7

Verifique que $u(x, y, t) = 2 \sin \left( \frac{x}{3} \right) \sin \left( \frac{y}{4} \right) e^{-25t/16}$ es una solución de la ecuación de calor

$$ u_t = 9(u_{xx} + u_{yy}). \hspace{20pt} \text{(11.3.10)} $$

♦

Dado que la solución de la ecuación del calor en dos dimensiones es una función de tres variables, no es sencillo crear una representación visual de la solución. Podemos graficar la solución para valores fijos de (t), lo que equivale a instantáneas de la distribución del calor en instantes determinados. Estas instantáneas muestran cómo se distribuye el calor sobre una superficie bidimensional a medida que transcurre el tiempo. La gráfica de la solución anterior en el instante (t = 0) aparece en la figura siguiente. A medida que el tiempo avanza, los valores extremos se atenúan, aproximándose a cero cuando (t) tiende a infinito.

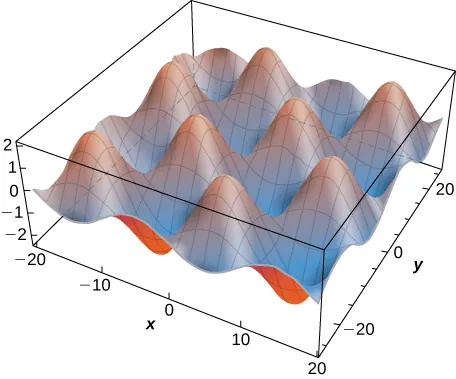
Si consideramos la ecuación de calor en una dimensión, es posible graficar la solución a lo largo del tiempo. La ecuación de calor en una dimensión se convierte en

$$ u_t = c^2 u_{xx}, $$

donde $c^2$ representa la difusividad térmica del material en cuestión. Una solución de esta ecuación diferencial puede escribirse de la forma

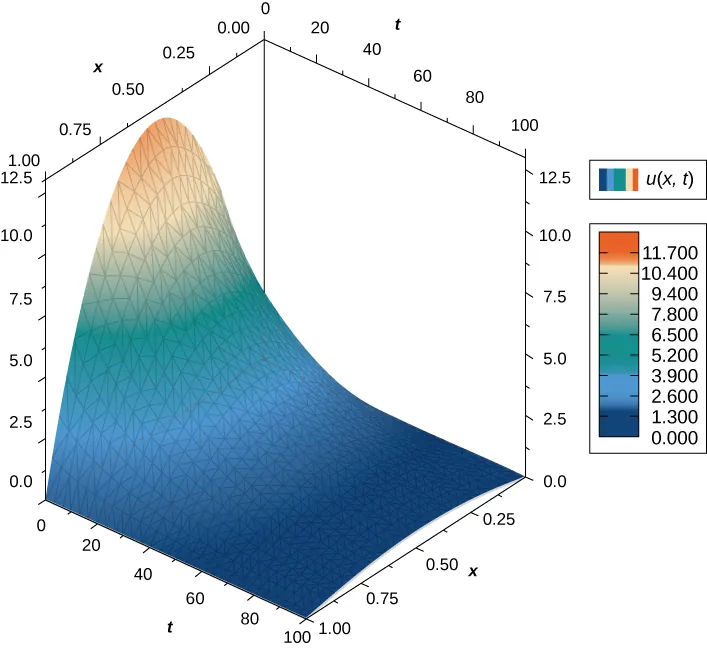
$$ u_m (x, t) = e^{-\pi^2 m^2 c^2 t} \sin (m\pi x) \hspace{20pt} \text{(11.3.11)} $$

donde $m$ es cualquier número entero positivo. Una gráfica de esta solución usando $m = 1$ aparece en la Figura 11.3.4, donde la distribución de temperatura inicial sobre un cable de longitud 1 está dada por $u(x, 0) = \sin \pi x$. Observe que a medida que el tiempo progresa, el cable se enfría. Esto se observa porque, de izquierda a derecha, la temperatura más alta (que ocurre en medio del cable) disminuye y cambia de color de rojo a azul.

Proyecto estudiantil

Lord Kelvin y la edad de la Tierra

Durante finales del siglo XIX, los científicos del nuevo campo de la geología estaban llegando a la conclusión de que la Tierra debía tener “millones y millones” de años de antigüedad. Aproximadamente al mismo tiempo, Charles Darwin había publicado su tratado sobre la evolución. La postura de Darwin era que la evolución necesitaba muchos millones de años para tener lugar, y realizó la audaz afirmación de que los campos de creta del Weald, donde se encontraron fósiles importantes, eran el resultado de 300 millones de años de erosión.

En esa época, el eminente físico William Thomson (Lord Kelvin) utilizó una importante ecuación diferencial parcial, conocida como la ecuación de difusión del calor, para estimar la edad de la Tierra determinando cuánto tiempo tardaría en enfriarse desde roca fundida hasta el estado que presentaba en ese momento. Su conclusión fue un intervalo de entre 20 y 400 millones de años, siendo lo más probable alrededor de 50 millones de años. Durante muchas décadas, las afirmaciones de este icono incuestionable de la ciencia no fueron bien recibidas ni por los geólogos ni por Darwin.

Kelvin hizo suposiciones razonables basadas en lo que se conocía en su época, pero también realizó varias suposiciones que resultaron ser incorrectas. Una suposición errónea fue considerar que la Tierra es sólida y que, por lo tanto, el enfriamiento se producía únicamente por conducción, lo que justificaba el uso de la ecuación de difusión. Sin embargo, el error más grave fue uno comprensible: la omisión del hecho de que la Tierra contiene elementos radiactivos que suministran calor de manera continua por debajo del manto terrestre. El descubrimiento de la radiactividad ocurrió cerca del final de la vida de Kelvin, y él reconoció que su cálculo tendría que ser modificado.

Kelvin utilizó un modelo unidimensional simple aplicado solo a la capa externa de la Tierra, y dedujo la edad a partir de gráficas y del gradiente de temperatura aproximadamente conocido cerca de la superficie terrestre. Consideremos ahora una versión más apropiada de la ecuación de difusión en coordenadas radiales, que tiene la forma

Aquí, $T(r, t)$ es la temperatura como función de $r$ (medida desde el centro de la Tierra) y el tiempo $t$. $K$ es la conductividad térmica — para roca fundida, en este caso. El método estándar para resolver tal ecuación diferencial parcial es por separación de variables, donde expresamos la solución como el producto de funciones que contienen cada variable por separado. En este caso, escribiríamos la temperatura como

$$ T(r, t) = R(r) f(t). $$

1. Sustituya esta forma en la Ecuación 11.3.2 y, observando que $f(t)$ es constante con respecto a la distancia ($r$) y $R(r)$ es constante con respecto al tiempo ($t$), demuestre que $$ \frac{1}{f} \frac{\partial f}{\partial t} = \frac{K}{R} \left[ \frac{\partial^2 R}{\partial r^2} + \frac{2}{r} \frac{\partial R}{\partial r} \right]. $$
2. Esta ecuación representa la separación de variables que deseamos. El lado izquierdo es solo una función de $t$ y el lado derecho es solo una función de $r$, y deben ser iguales para todos los valores de $r$ y $t$. Por lo tanto, ambos deben ser iguales a una constante. Llamemos a esa constante $-\lambda^2$. (La conveniencia de esta elección se ve al sustituir). Entonces, tenemos $$ \frac{1}{f} \frac{\partial f}{\partial t} = -\lambda^2 \quad \text{y} \quad \frac{K}{R} \left[ \frac{\partial^2 R}{\partial r^2} + \frac{2}{r} \frac{\partial R}{\partial r} \right] = -\lambda^2. $$

Ahora, podemos verificar mediante sustitución directa para cada ecuación que las soluciones son $f(t) = Ae^{-\lambda^2 t}$ y $R(r) = B \left( \frac{\sin \alpha r}{r} \right) + C \left( \frac{\cos \alpha r}{r} \right)$, donde $\alpha = \lambda / \sqrt{K}$. Note que $f(t) = Ae^{+\lambda^2 t}$ también es una solución válida, ¿así que podríamos haber elegido $+\lambda^2$ para nuestra constante. ¿Puede ver por qué no sería válida para este caso a medida que el tiempo aumenta?

3. Apliquemos ahora las condiciones de contorno.
   1. La temperatura debe ser finita en el centro de la Tierra, $r = 0$. ¿Cuál de las dos constantes, $B$ o $C$, debe por lo tanto ser cero para mantener a $R$ finita en $r = 0$? (Recuerde que $\sin(\alpha r)/r \to \alpha$ cuando $r \to 0$, pero $\cos(\alpha r)/r$ se comporta de manera muy diferente).
   2. Kelvin argumentó que cuando el magma alcanza la superficie de la Tierra, se enfría muy rápidamente. Una persona a menudo puede tocar la superficie a las pocas semanas del flujo. Por lo tanto, la superficie alcanzó una temperatura moderada muy pronto y permaneció casi constante a una temperatura superficial $T_s$. Por simplicidad, establezcamos $T = 0$ en $r = R_E$ y encontremos una $\alpha$ tal que esta sea la temperatura para todo tiempo $t$. (Kelvin tomó el valor de $300 \text{ K} \approx 80^\circ\text{F}$. Podemos añadir esta constante de $300 \text{ K}$ a nuestra solución más tarde). Para que esto sea cierto, el argumento del seno debe ser cero en $r = R_E$. Note que $\alpha$ tiene una serie infinita de valores que satisfacen esta condición. Cada valor de $\alpha$ representa una solución válida (cada uno con su propio valor para $A$). La solución total o general es la suma de todas estas soluciones.
   3. En $t = 0$, asumimos que toda la Tierra estaba a una temperatura caliente inicial $T_0$ (Kelvin tomó esto como aproximadamente $7000 \text{ K}$). La aplicación de esta condición de contorno implica la aplicación más avanzada de los coeficientes de Fourier. Como se señaló en la parte b, cada valor de $\alpha_n$ representa una solución válida, y la solución general es una suma de todas estas soluciones. Esto resulta en una solución en serie:

$$ T(r, t) = \left( \frac{T_0 R_E}{\pi} \right) \sum_n \frac{(-1)^{n-1}}{n} e^{-\lambda n^2 t} \frac{\sin(\alpha_n r)}{r}, \text{ donde } \alpha_n = n\pi/R_E. $$

Observe cómo los valores de $\alpha_n$ provienen de la condición de contorno aplicada en la parte b. El término $\frac{(-1)^{n-1}}{n}$ es la constante $A_n$ para cada término de la serie, determinada al aplicar el método de Fourier. Dejando $\beta = \frac{\pi}{R_E}$, examine los primeros términos de esta solución mostrada aquí y observe cómo $\lambda^2$ en la exponencial hace que los términos de orden superior disminuyan rápidamente a medida que el tiempo progresa:

$$ T(r, t) = \frac{T_0 R_E}{\pi r} \left( e^{-K\beta^2 t} (\sin \beta r) – \frac{1}{2} e^{-4K\beta^2 t} (\sin 2\beta r) + \frac{1}{3} e^{-9K\beta^2 t} (\sin 3\beta r) \dots \right) $$

Cerca del tiempo $t = 0$, se necesitan muchos términos de la solución para obtener precisión. Insertando valores para la conductividad $K$ y $\beta = \pi/R_E$ para tiempos que se aproximan a apenas miles de años, solo los primeros términos hacen una contribución significativa. Kelvin solo necesitó mirar la solución cerca de la superficie de la Tierra (Figura 11.3.6) y, después de mucho tiempo, determinar qué tiempo producía mejor el gradiente de temperatura estimado conocido durante su época ($1^\circ\text{F}$ de aumento por cada 50 pies). Simplemente eligió un rango de tiempos con un gradiente cercano a este valor. En la Figura 11.3.6, las soluciones se grafican y escalan, con la temperatura superficial de $300 \text{ K}$ añadida. Note que el centro de la Tierra estaría relativamente frío. En ese momento, se pensaba que la Tierra debía ser sólida.

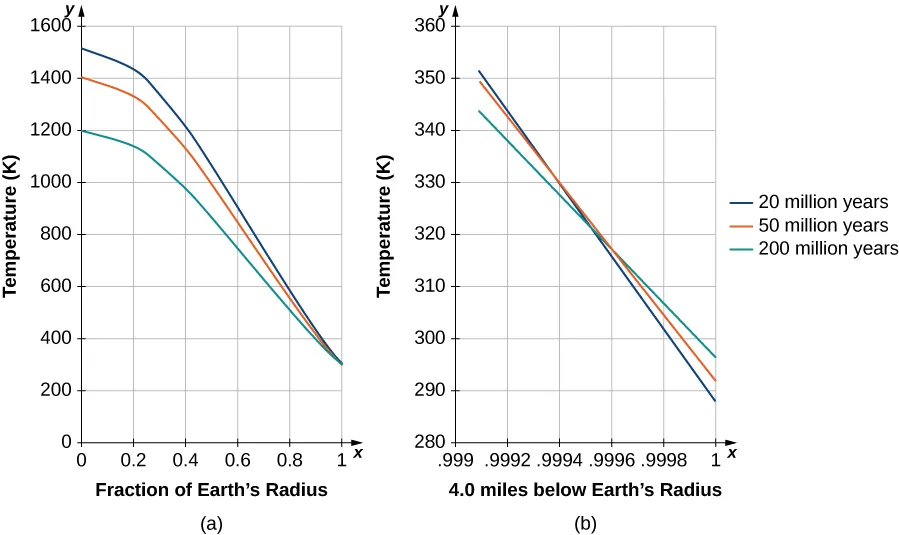
Epílogo:

El 20 de mayo de 1904, el físico Ernest Rutherford habló en la Royal Institution para anunciar un cálculo revisado que incluía la contribución de la radiactividad como fuente del calor de la Tierra. En palabras del propio Rutherford:

«Entré en la sala, que estaba a media luz, y pronto distinguí a Lord Kelvin entre el público, y me di cuenta de que me esperaban problemas en la última parte de mi discurso, dedicada a la edad de la Tierra, donde mis opiniones entraban en conflicto con las suyas. Para mi alivio, Kelvin se quedó profundamente dormido, pero cuando llegué al punto importante, vi al viejo pájaro incorporarse, abrir un ojo y lanzarme una mirada amenazadora.

Entonces me vino una inspiración repentina y dije que Lord Kelvin había limitado la edad de la Tierra, siempre que no se descubriera ninguna nueva fuente [de calor]. Esa declaración profética se refería a lo que estamos considerando esta noche: ¡el radio! ¡He aquí! El anciano me sonrió complacido».

Rutherford calculó una edad para la Tierra de aproximadamente 500 millones de años. En la actualidad, el valor aceptado de la edad de la Tierra es de alrededor de 4.6 mil millones de años. ♦