| 11. Diferenciación de funciones de varias variables | 11.3 Derivadas parciales |
Ejercicios propuestos para el Capítulo 11.3
Para los siguientes ejercicios, calcule la derivada parcial utilizando únicamente las definiciones de límite.
112. $\frac{\partial z}{\partial x}$ para $z = x^2 – 3xy + y^2$
113. $\frac{\partial z}{\partial y}$ para $z = x^2 – 3xy + y^2$
Para los siguientes ejercicios, determine el signo de la derivada parcial utilizando la gráfica de la superficie.
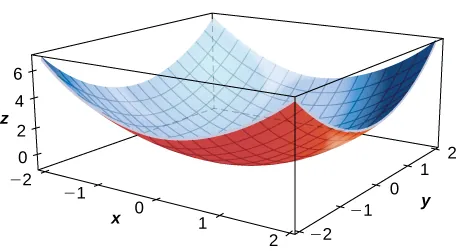
114. $f_x(1, 1)$
115. $f_x(-1, 1)$
116. $f_y(1, 1)$
117. $f_x(0, 0)$
Para los siguientes ejercicios, calcule las derivadas parciales.
118. $\frac{\partial z}{\partial x}$ para $z = \sin(3x)\cos(3y)$
119. $\frac{\partial z}{\partial y}$ para $z = \sin(3x)\cos(3y)$
120. $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$ para $z = x^8 e^{3y}$
121. $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$ para $z = \ln(x^6 + y^4)$
122. Halle $f_y(x, y)$ para $f(x, y) = e^{xy} \cos(x) \sin(y)$
123. Sea $z = e^{xy}$. Halle $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$.
124. Sea $z = \ln\left(\frac{x}{y}\right)$. Halle $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$.
125. Sea $z = \tan(2x – y)$. Halle $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$.
126. Sea $z = \sinh(2x + 3y)$. Halle $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$.
127. Sea $f(x, y) = \arctan\left(\frac{y}{x}\right)$. Evalúe $f_x(2, -2)$ y $f_y(2, -2)$.
128. Sea $f(x, y) = \frac{xy}{x – y}$. Halle $f_x(2, -2)$ y $f_y(2, -2)$.
129. Halle $\frac{\partial z}{\partial x}$ en $(0, 1)$ para $z = e^{-x} \cos(y)$. Evalúe las derivadas parciales en el punto $P(0, 1)$.
130. Dado $f(x, y, z) = x^3 y z^2$, halle $\frac{\partial^2 f}{\partial x \partial y}$ y $f_z(1, 1, 1)$.
131. Dado $f(x, y, z) = 2 \sin(x + y)$, halle $f_x(0, \frac{\pi}{2}, -4)$, $f_y(0, \frac{\pi}{2}, -4)$, y $f_z(0, \frac{\pi}{2}, -4)$.
132. El área de un paralelogramo con longitudes de lados adyacentes $a$ y $b$, y en el cual el ángulo entre estos dos lados es $\theta$, está dada por la función $A(a, b, \theta) = ba \sin(\theta)$. Halle la tasa de cambio del área del paralelogramo con respecto a lo siguiente:
- Lado $a$
- Lado $b$
- Ángulo $\theta$
133. Exprese el volumen de un cilindro circular recto como una función de dos variables:
- Su radio $r$ y su altura $h$.
- Demuestre que la tasa de cambio del volumen del cilindro con respecto a su radio es el producto de su circunferencia multiplicada por su altura.
- Demuestre que la tasa de cambio del volumen del cilindro con respecto a su altura es igual al área de la base circular.
134. Calcule $\frac{\partial w}{\partial z}$ para $w = z \sin(xy^2 + 2z)$.
Halle las derivadas parciales de orden superior indicadas.
135. $f_{xy}$ para $z = \ln(x – y)$
136. $f_{yx}$ para $z = \ln(x – y)$
137. Sea $z = x^2 + 3xy + 2y^2$. Halle $\frac{\partial^2 z}{\partial x^2}$ y $\frac{\partial^2 z}{\partial y^2}$.
138. Dado $z = e^x \tan y$, halle $\frac{\partial^2 z}{\partial x \partial y}$ y $\frac{\partial^2 z}{\partial y \partial x}$.
139. Dado $f(x, y, z) = xyz$, halle $f_{xyy}$, $f_{yxy}$, y $f_{yyx}$.
140. Dado $f(x, y, z) = e^{-2x} \sin(z^2 y)$, demuestre que $f_{xyy} = f_{yxy}$.
141. Demuestre que $z = \frac{1}{2}(e^y – e^{-y}) \sin x$ es una solución de la ecuación diferencial $\frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2} = 0$.
142. Halle $f_{xx}(x, y)$ para $f(x, y) = \frac{4x^2}{y} + \frac{y^2}{2x}$.
143. Sea $f(x, y, z) = x^2 y^3 z – 3xy^2 z^3 + 5x^2 z – y^3 z$. Halle $f_{xyz}$.
144. Sea $F(x, y, z) = x^3 yz^2 – 2x^2 yz + 3xz – 2y^3 z$. Halle $F_{xyz}$.
145. Dado $f(x, y) = x^2 + x – 3xy + y^3 – 5$, halle todos los puntos en los que $f_x = f_y = 0$ simultáneamente.
146. Dado $f(x, y) = 2x^2 + 2xy + y^2 + 2x – 3$, halle todos los puntos en los que $\frac{\partial f}{\partial x} = 0$ y $\frac{\partial f}{\partial y} = 0$ simultáneamente.
147. Dado $f(x, y) = y^3 – 3yx^2 – 3y^2 – 3x^2 + 1$, halle todos los puntos en $f$ en los que $f_x = f_y = 0$ simultáneamente.
148. Dado $f(x, y) = 15x^3 – 3xy + 15y^3$, halle todos los puntos en los que $f_x(x, y) = f_y(x, y) = 0$ simultáneamente.
149. Demuestre que $z = e^x \sin y$ satisface la ecuación $\frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2} = 0$.
150. Demuestre que $f(x, y) = \ln(x^2 + y^2)$ resuelve la ecuación de Laplace $\frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2} = 0$.
151. Demuestre que $z = e^{-t} \cos\left(\frac{x}{c}\right)$ satisface la ecuación de calor $\frac{\partial z}{\partial t} = c^2 \left(\frac{\partial^2 z}{\partial x^2}\right)$.
152. Halle $\lim_{\Delta x \to 0} \frac{f(x+\Delta x, y) – f(x, y)}{\Delta x}$ para $f(x, y) = -7x – 2xy + 7y$.
153. Halle $\lim_{\Delta y \to 0} \frac{f(x, y+\Delta y) – f(x, y)}{\Delta y}$ para $f(x, y) = -7x – 2xy + 7y$.
154. Halle $\lim_{\Delta x \to 0} \frac{\Delta f}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x+\Delta x, y) – f(x, y)}{\Delta x}$ para $f(x, y) = x^2 y^2 + xy + y$.
155. Halle $\lim_{\Delta x \to 0} \frac{\Delta f}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x+\Delta x, y) – f(x, y)}{\Delta x}$ para $f(x, y) = \sin(xy)$.
156. La función $P(T, V) = \frac{nRT}{V}$ da la presión en un punto de un gas como función de la temperatura $T$ y el volumen $V$. Las letras $n$ y $R$ son constantes. Halle $\frac{\partial P}{\partial V}$ y $\frac{\partial P}{\partial T}$, y explique qué representan estas cantidades.
157. La ecuación para el flujo de calor en el plano $xy$ es $\frac{\partial f}{\partial t} = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$. Demuestre que $f(x, y, t) = e^{-2t} \sin x \sin y$ es una solución.
158. La ecuación de onda básica es $f_{tt} = f_{xx}$. Verifique que $f(x, t) = \sin(x + t)$ y $f(x, t) = \sin(x – t)$ son soluciones.
159. La ley de los cosenos puede pensarse como una función de tres variables. Sean $x$, $y$ y $\theta$ dos lados de cualquier triángulo donde el ángulo $\theta$ es el ángulo incluido entre los dos lados. Entonces, $F(x, y, \theta) = x^2 + y^2 – 2xy \cos \theta$ da el cuadrado del tercer lado del triángulo. Halle $\frac{\partial F}{\partial \theta}$ y $\frac{\partial F}{\partial x}$ cuando $x = 2, y = 3$ y $\theta = \frac{\pi}{6}$.
160. Suponga que los lados de un rectángulo están cambiando con respecto al tiempo. El primer lado está cambiando a una tasa de $2$ pulg./seg., mientras que el segundo lado está cambiando a una tasa de $4$ pulg./seg. ¿Qué tan rápido está cambiando la diagonal del rectángulo cuando el primer lado mide $16$ pulg. y el segundo mide $20$ pulg.? (Redondee la respuesta a tres decimales).
161. Una función de producción Cobb-Douglas es $f(x, y) = 200x^{0.7}y^{0.3}$, donde $x$ e $y$ representan la cantidad de mano de obra y capital disponible. Sea $x = 500$ y $y = 1000$. Halle $\frac{\partial f}{\partial x}$ y $\frac{\partial f}{\partial y}$ en estos valores, las cuales representan la productividad marginal de la mano de obra y del capital, respectivamente.
162. El índice de temperatura aparente es una medida de cómo se siente la temperatura y se basa en dos variables: $h$, que es la humedad relativa, y $t$, que es la temperatura del aire.
$$ A = 0.885t – 22.4h + 1.20th – 0.544. $$Halle $\frac{\partial A}{\partial t}$ y $\frac{\partial A}{\partial h}$ cuando $t = 20^\circ\text{F}$ y $h = 0.90$.
