| 6. Aplicaciones de la integral | Ejercicios propuestos para el capítulo 6.3 |
6.3 Volúmenes de revolución. Capas cilíndricas
Objetivos de aprendizaje:
6.3.1. Calcular el volumen de un sólido de revolución utilizando el método de las capas cilíndricas.
6.3.2. Comparar los diferentes métodos para calcular un volumen de revolución.
En la presente sección, examinamos el método de capas cilíndricas, el último método que vamos a estudiar para calcular la medida del volumen de un sólido de revolución. Podemos usar este método en los mismos tipos de sólidos que el método de disco o el método de las arandelas; sin embargo, con los métodos de disco y arandela, nosotros integramos a lo largo del eje de coordenadas paralelo al eje de revolución. Con el método de capas cilíndricas, integramos a lo largo del eje de coordenadas perpendicular al eje de revolución. La capacidad de elegir qué variable de integración queremos usar puede ser una ventaja significativa con funciones más complicadas. Además, la geometría específica del sólido a veces hace que el método de usar capas cilíndricas sea más atractivo que usar el método de arandela. En la última parte de esta sección, revisamos todos los métodos para encontrar el volumen que hemos estudiado y presentamos algunas pautas para ayudarlo a determinar qué método usar en una situación dada.
El método de las capas cilíndricas
Nuevamente, estamos trabajando con un sólido de revolución. Como antes, definimos una región R, acotada arriba por la gráfica de una función y = f (x), abajo por el eje x y a la izquierda y derecha por las rectas x = a y x = b, respectivamente, como se muestra en la Figura 6.3_1 (a). Luego giramos esta región alrededor del eje y, como se muestra en la Figura 6.3_1 (b). Tenga en cuenta que esto es diferente de lo que hemos hecho antes. Anteriormente, las regiones definidas en términos de funciones de x giraban alrededor del eje x o una línea paralela a él.

Como lo hemos hecho muchas veces antes, “particionamos” el intervalo cerrado [a, b] usando una partición regular, P = {x0, x1, …, xn} y, para i = 1, 2, …, n, elija un punto xi* ∈ [xi − 1, xi]. Luego, construya un rectángulo sobre el intervalo [xi − 1, xi] de altura f (xi*) y ancho Δx. Un rectángulo representativo se muestra en la Figura 6.3_2 (a). Cuando ese rectángulo gira alrededor del eje y, en lugar de un disco o una arandela, obtenemos una cáscara cilíndrica, como se muestra en la siguiente figura.
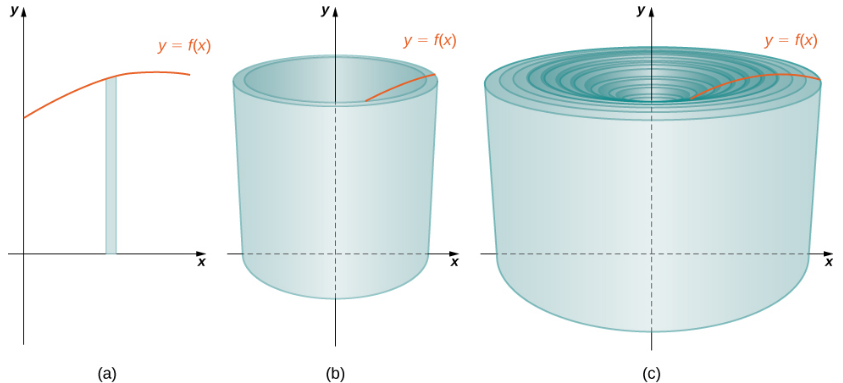
(Figura 6.3_2 (a) Un rectángulo representativo. (b) Cuando este rectángulo gira alrededor del eje y, el resultado es una cáscara cilíndrica. (c) Cuando juntamos todas las capas, obtenemos una aproximación del sólido original.)
Para calcular el volumen de este caparazón (carcasa, cáscara), considere la Figura 6.3_3.

La carcasa es un cilindro, por lo que su volumen es el área de la sección transversal multiplicada por la altura del cilindro. Las secciones transversales son anillos (regiones en forma de anillo, esencialmente círculos con un orificio en el centro), con radio externo xi y radio interno xi − 1. Por lo tanto, el área de la sección transversal es

La altura del cilindro es f (xi*). Entonces el volumen V del caparazón es

Tenga en cuenta que si xi − xi − 1 = Δx, entonces tenemos

Además, (xi − xi − 1)/2 es tanto el punto medio del intervalo [xi − 1, xi] como el radio promedio del cascarón, y podemos aproximar esto por xi*. Entonces tenemos

Otra forma de pensar en esto es imaginar en hacer un corte vertical en el caparazón y luego abrirlo para formar una placa plana (Figura 6.3_4).

En realidad, el radio exterior de la carcasa es mayor que el radio interior y, por lo tanto, el borde posterior de la placa sería ligeramente más largo que el borde frontal de la placa. Sin embargo, podemos aproximar la carcasa aplanada por una placa plana de altura f (xi*), ancho 2π xi* y espesor Δx (Figura 6.3_4). El volumen de la carcasa, entonces, es aproximadamente el volumen de la placa plana. Multiplicando la altura, el ancho y la profundidad de la placa, obtenemos

que es la misma fórmula que teníamos antes.
Para calcular el volumen de todo el sólido, agregamos los volúmenes de todas las capas y obtenemos

Aquí tenemos otra suma de Riemann, esta vez para la función 2πx f(x). Tomar el límite cuando n → ∞ nos da

Esto lleva a la siguiente regla para el método de las capas cilíndricas.
Regla 6.3.1: EL Método de las capas cilíndricas
Sea f (x) una función continua y no negativa. Y sea R la región delimitada arriba por la gráfica de f (x), abajo por el eje x, a la izquierda por la recta x = a, y a la derecha por la recta x = b. Entonces el volumen del sólido de revolución formado al girar R alrededor del eje y está dado por
\( V = \int_a^b (2 \pi x f(x)) dx. \)
Ejemplo ilustrativo 6.3_1. El método de las carcasas cilíndricas 1
Defina R como la región acotada arriba por la gráfica de f (x) = 1/x y abajo por el eje x sobre el intervalo [1, 3]. Encuentre el volumen del sólido de revolución formado al girar R alrededor del eje y.
Solución:
Primero debemos graficar la región R y el sólido de revolución asociado, como se muestra en la siguiente figura.
(Figura 6.3_5 (a) La región R debajo de la gráfica de f (x) = 1/x en el intervalo [1, 3]. (b) El sólido de revolución generado al girar R alrededor del eje y.)
Entonces el volumen del sólido viene dado por
♦
Ejercicio de control 6.3_1
Defina R como la región acotada arriba por la gráfica de f (x) = x2 y abajo por el eje x sobre el intervalo [1, 2]. Encuentre el volumen del sólido de revolución formado al girar R alrededor del eje y. ♦
Ejemplo ilustrativo 6.3_2. El método de las carcasas cilíndricas 2
Defina R como la región acotada arriba por la gráfica de f (x) = 2x − x2 y abajo por el eje x sobre el intervalo [0, 2]. Encuentre el volumen del sólido de revolución formado al girar R alrededor del eje y.
Solución:
Primero grafique la región R y el sólido de revolución asociado, como se muestra en la siguiente figura.
(Figura 6.3_6 (a) La región R bajo la gráfica de f (x) = 2x − x2 sobre el intervalo [0, 2]. (b) El volumen de revolución obtenido al girar R alrededor del eje y.)
Entonces el volumen del sólido viene dado por
♦
Ejercicio de control 6.3_2
Defina R como la región acotada arriba por la gráfica de f (x) = 3x − x2 y abajo por el eje x sobre el intervalo [0, 2]. Encuentre el volumen del sólido de revolución formado al girar R alrededor del eje y. ♦
Al igual que con el método del disco y el método de la arandela, podemos usar el método de capas cilíndricas con sólidos de revolución, girados alrededor del eje x, cuando queremos integrar con respecto a y. La regla análoga para este tipo de sólido se da a continuación.
Regla 6.3.2: El método de capas cilíndricas para sólidos de revolución alrededor del eje x
Sea g(y) una función continua y no negativa. Y sea Q la región delimitada a la derecha por la gráfica de g(y), a la izquierda por el eje y, debajo por la recta y = c, y arriba por la recta y = d. Entonces, el volumen del sólido de revolución formado al girar Q alrededor del eje x viene dado por
\( V = \int_c^d (2 \pi y g(y)) dy. \)
♦
Ejemplo ilustrativo 6.3_3. El método de conchas cilíndricas para un sólido que gira alrededor del eje x
Defina Q como la región limitada a la derecha por la gráfica de g (y) = 2√y y a la izquierda por el eje y para y ∈ [0, 4]. Encuentre el volumen del sólido de revolución formado al girar Q alrededor del eje x.
Solución:
Primero, necesitamos graficar la región Q y el sólido de revolución asociado, como se muestra en la siguiente figura.
(Figura 6.3_7 (a) La región Q a la izquierda de la función g(y) sobre el intervalo [0, 4]. (b) El sólido de revolución generado al girar Q alrededor del eje x.)
El volumen del sólido viene dado por

♦
Ejercicio de control 6.3_3
Defina Q como la región limitada a la derecha por la gráfica de g(y) = 3/y y a la izquierda por el eje y para y ∈ [1, 3]. Encuentre el volumen del sólido de revolución formado al girar Q alrededor del eje x. ♦
¿Qué método debemos usar?
Hemos estudiado varios métodos para encontrar el volumen de un sólido de revolución, pero ¿cómo sabemos qué método usar? A menudo se trata de elegir qué integral es más fácil de evaluar. La figura 6.13 describe los diferentes enfoques para los sólidos de revolución alrededor del eje x.
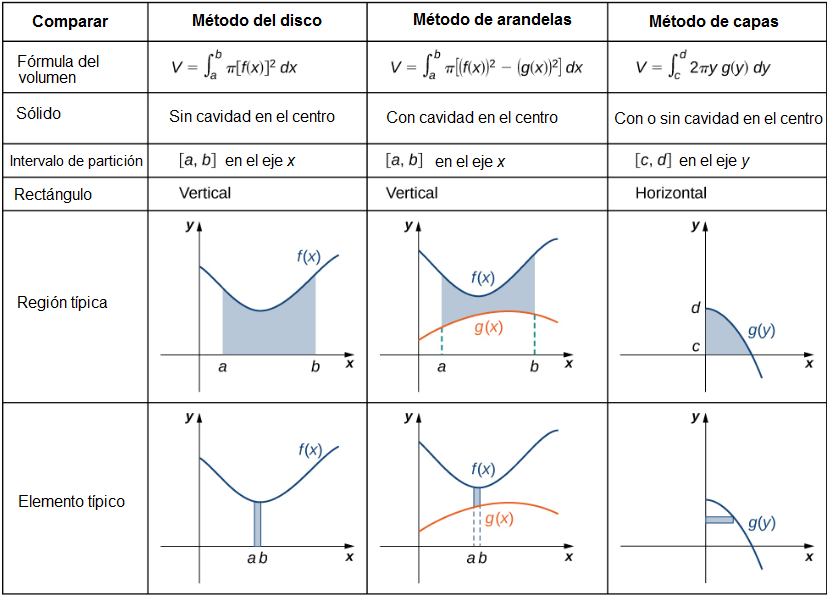
Echemos un vistazo a un par de problemas adicionales y decidamos cuál es el mejor enfoque para resolverlos.
Ejemplo ilustrativo 6.3.4: Seleccionando el Mejor Método
Para cada uno de los siguientes problemas, seleccione el mejor método para encontrar el volumen de un sólido de revolución generado al girar la región dada alrededor del eje x, y establezca la integral para encontrar el volumen (no evalúe la integral).
- La región delimitada por las gráficas de \( y = x \), \( y = 2 – x \), y el eje x.
- La región delimitada por las gráficas de \( y = 4x – x^2 \) y el eje x.
Solución:
a. Primero, dibuje la región y el sólido de revolución como se muestra en la siguiente imagen:
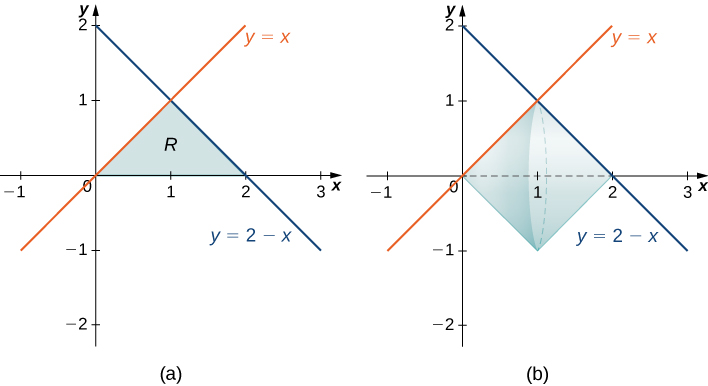
Figura 6.3.9 (a) La región R limitada por dos líneas y el eje x. (b) El sólido de revolución generado al girar R alrededor del eje x.
Mirando la región, si quisiéramos integrar con respecto a *x*, tendríamos que dividir la integral en dos partes, porque tenemos diferentes funciones que limitan la región sobre [0, 1] y [1, 2]. En este caso, usando el método del disco, tendríamos
\( V = \int_0^1 (\pi x^2) \, dx + \int_1^2 (\pi (2 – x)^2) \, dx. \)
Si usáramos el método de la cáscara en su lugar, usaríamos funciones de *y* para representar las curvas, produciendo
\( \begin{aligned} V &= \int_0^1 (2 \pi y [(2 – y) – y]) \, dy \\ &= \int_0^1 (2 \pi y [2 – 2y]) \, dy. \end{aligned} \)
Ninguna de estas integrales es particularmente onerosa, pero dado que el método de la cáscara requiere solo una integral, y el integrando requiere menos simplificación, probablemente deberíamos optar por el método de la cáscara en este caso.
b. Primero, dibuja la región y el sólido de revolución como se muestra en la siguiente figura:
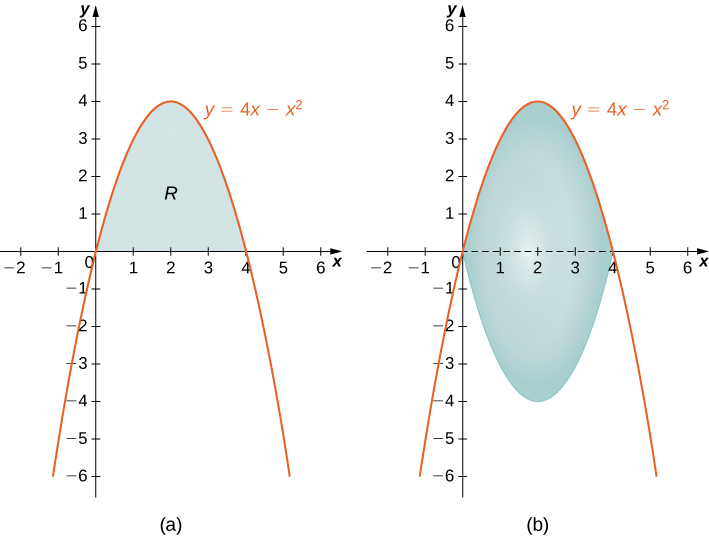
Figura 6.3.10 (a) La región R entre la curva y el eje x. (b) El sólido de revolución generado al girar R alrededor del eje x.
Mirando la región, sería problemático definir un rectángulo horizontal; la región está delimitada a la izquierda y a la derecha por la misma función. Por lo tanto, podemos descartar el método de las cáscaras. El sólido no tiene cavidad en el medio, por lo que podemos usar el método de los discos. Entonces
\( V = \int_0^4 \pi (4x – x^2)^2 \, dx. \)
♦
Ejercicio de control 6.3_4
Seleccione el mejor método para encontrar el volumen de un sólido de revolución generado al girar la región dada alrededor del eje x, y establezca la integral para encontrar el volumen (no evalúe la integral): la región delimitada por las gráficas de \( y = 2 – x^2 \) e \( y = x^2 \). ♦

muy bueno gracias por la explicacion
👍
muy bueno
Gracias por comentar! 👍😺