| 5. La integral y Técnicas de integración | Ejercicios propuestos para el Capítulo 5.9 |

5.9 Integrales trigonométricas

Objetivos de aprendizaje:

5.9.1. Resolver problemas de integración que involucran productos y potencias de senx y cosx.
5.9.2. Resuelva problemas de integración que involucran productos y potencias de tanx y secx.
5.9.3. Use fórmulas de reducción para resolver integrales trigonométricas.

    En esta sección veremos cómo integrar una variedad de productos de funciones trigonométricas. Estas integrales se llaman integrales trigonométricas. Son una parte importante de la técnica de integración llamada sustitución trigonométrica. Esta técnica nos permite convertir expresiones algebraicas que quizás no podamos integrar en expresiones que involucren funciones trigonométricas, que podemos integrar utilizando las técnicas descritas en esta sección. Además, este tipo de integrales aparecen con frecuencia cuando estudiamos sistemas de coordenadas polares, cilíndricas y esféricas más adelante. Comencemos nuestro estudio con productos de senx y cosx.

Integrando productos y potencias de senx y cosx

Una idea clave detrás de la estrategia utilizada para integrar combinaciones de productos y potencias de senx y cosx implica reescribir estas expresiones como sumas y diferencias de integrales de la forma ∫senʲxcosxdx o ∫cosʲxsenxdx. Después de reescribir estas integrales, las evaluamos usando la sustitución u. Antes de describir el proceso general en detalle, echemos un vistazo a los siguientes ejemplos.

EJEMPLO ILUSTRATIVO 5.9_1. Integrando de la forma ∫cosʲxsenxdx

Evalúe ∫cos³x senxdx.

Solución:
Utilice la sustitución u tomando u = cosx. En este caso, du = −senxdx. Así,

♦

Ejercicio de control 5.9.l 

Evalúe $\int \sin^4 x \cos x \, dx$. ♦

EJEMPLO ILUSTRATIVO 5.9_2. Un ejemplo preliminar: integración de ∫cosʲxsenᴷxdx donde k es impar

Evalúe ∫cos²x sen³xdx.

Solución:
Para convertir esta integral en integrales de la forma ∫cosʲx senxdx, reescribe sen³x = sen²xsenx y realiza la sustitución sen²x = 1 − cos²x. Así,

Ahora, sea u = cosx; entonces du = −senxdx, de tal manera que:

♦

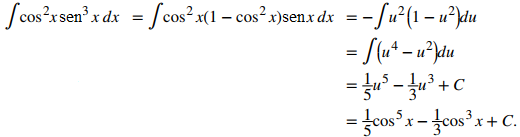Ejercicio de control 5.9.2

Evalúe $\int \cos^3 x \sin^2 x \, dx$. ♦

       En el siguiente ejemplo, vemos la estrategia que debe aplicarse cuando solo hay potencias pares de senx y cosx. Para integrales de este tipo, las identidades

son invaluables Estas identidades a veces se conocen como identidades reductoras de potencia y pueden derivarse de la identidad de doble ángulo cos(2x) = cos²x − sen²x y la identidad pitagórica cos²x + sen²x = 1.

EJEMPLO ILUSTRATIVO 5.9_3. Integrando una potencia uniforme de senx

Evaluar ∫sen²xdx.

Solución:
Para evaluar esta integral, usemos la identidad trigonométrica sen²x = 1/2 − (1/2)cos(2x). Así,

♦

Ejercicio de control 5.9.3

Evalúe $\int \cos^2 x \, dx$. ♦

El proceso general para integrar productos de potencias de senx y cosx se resume en el siguiente conjunto de pautas.

ESTRATEGIA PARA RESOLVER PROBLEMAS: INTEGRANDO PRODUCTOS Y POTENCIAS DE SENX Y COSX

Para integrar $\int \cos^j x \sin^k x \, dx$ use las siguientes estrategias:

1. Si \(k\) es impar, reescriba $\sin^k x = \sin^{k-1} x \sin x$ y use la identidad $\sin^2 x = 1 – \cos^2 x$ para reescribir $\sin^{k-1} x$ en términos de $\cos x$. Integre usando la sustitución $u = \cos x$. Esta sustitución hace $du = -\sin x \, dx$.
2. Si \(j\) es impar, reescriba $\cos^j x = \cos^{j-1} x \cos x$ y use la identidad $\cos^2 x = 1 – \sin^2 x$ para reescribir $\cos^{j-1} x$ en términos de $\sin x$. Integre usando la sustitución $u = \sin x$. Esta sustitución hace $du = \cos x \, dx$. (Nota: Si tanto \(j\) como \(k\) son impares, se puede usar la estrategia 1 o la estrategia 2).
3. Si tanto \(j\) como \(k\) son pares, use $\sin^2 x = (1/2) – (1/2)\cos(2x)$ y $\cos^2 x = (1/2) + (1/2)\cos(2x)$. Después de aplicar estas fórmulas, simplifique y vuelva a aplicar las estrategias 1 a 3 según corresponda. ♦

EJEMPLO ILUSTRATIVO 5.9_4. Integrando ∫cosʲx senᴷx dx donde k es impar

Evalúe ∫cos⁸x sen⁵xdx.

Solución:
Como la potencia de senx es impar, use la estrategia 1. Por lo tanto,

♦

EJEMPLO ILUSTRATIVO 5.9_5. Integrando ∫cosʲx senᴷx dx donde k es par

Evaluar ∫sen⁴xdx.

Solución:
Como la potencia en senx es par (k = 4) y la potencia en cosx es par (j = 0), debemos usar la estrategia 3. Por lo tanto,

Como cos²(2x) tiene una potencia par, sustituya cos²(2x) = 1/2 + (1/2)cos (4x):

♦

Ejercicio de control 5.9.4

Evalúe $\int \cos^3 x \, dx$. ♦

Ejercicio de control 5.9.5

Evalúe $\int \cos^2(3x) \, dx$. ♦

       En algunas áreas de la física, como la mecánica cuántica, el procesamiento de señales y el cálculo de las series de Fourier, a menudo es necesario integrar productos que incluyen sen(ax), sen(bx), cos(ax) y cos(bx). Estas integrales se evalúan aplicando identidades trigonométricas, como se describe en la siguiente regla.

REGLA 5.9.1: INTEGRAR PRODUCTOS DE SENOS Y COSENOS DE DIFERENTES ÁNGULOS

Para integrar productos que involucren $\sin(ax)$, $\sin(bx)$, $\cos(ax)$ y $\cos(bx)$, use las sustituciones:

♦

Estas fórmulas pueden deducirse de las fórmulas de suma de ángulos para seno y coseno.

EJEMPLO ILUSTRATIVO 5.9_6. Evaluación de la forma ∫sen(ax) cos(bx) dx

Evalúe ∫sen(5x) cos(3x)dx.

Solución:
Aplique la identidad sen(5x) cos(3x) = 12sen(2x) − 12sen(8x). Así,

♦

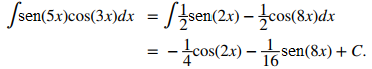Ejercicio de control 5.9.6

Evalúe $\int \cos(6x) \cos(5x) \, dx$. ♦

Integrando productos y potencias de tanx y secx

Antes de discutir la integración de productos y potenciass de tanx y secx, es útil recordar las integrales que involucran tanx y secx que ya hemos aprendido que:

Para la mayoría de las integrales de productos y potencias de tanx y secx, reescribimos la expresión que deseamos integrar como la suma o diferencia de integrales de la forma ∫tanʲxsec²xdx o ∫secʲxtanxdx. Como vemos en el siguiente ejemplo, podemos evaluar estas nuevas integrales usando la sustitución u.

EJEMPLO ILUSTRATIVO 5.9_7. Evaluación de ∫secʲxtanx dx

Evalúe ∫sec⁵x tanx dx.

Solución:
Comience reescribiendo sec⁵xtanx como sec⁴xsecxtanx.

♦

Ejercicio de control 5.9.7

Evalúe $\int \tan^5 x \sec^2 x \, dx$. ♦

       Ahora echamos un vistazo a las diversas estrategias para integrar productos y potencias de secx y tanx.

ESTRATEGIA PARA RESOLVER PROBLEMAS: INTEGRAR ∫tanᴷxsecᴶxdx

Para integrar $\int \tan^k x \sec^j x \, dx$, use las siguientes estrategias:

1. Si \(j\) es par y \(j \ge 2\), reescriba $\sec^j x = \sec^{j-2} x \sec^2 x$ y use $\sec^2 x = \tan^2 x + 1$ para reescribir $\sec^{j-2} x$ en términos de $\tan x$. Sea $u = \tan x$ y $du = \sec^2 x \, dx$.
2. Si \(k\) es impar y \(j \ge 1\), reescriba $\tan^k x \sec^j x = \tan^{k-1} x \sec^{j-1} x \sec x \tan x$ y use $\tan^2 x = \sec^2 x – 1$ para reescribir $\tan^{k-1} x$ en términos de $\sec x$. Sea $u = \sec x$ y $du = \sec x \tan x \, dx$. (Nota: Si \(j\) es par y \(k\) es impar, se puede usar la estrategia 1 o la estrategia 2).
3. Si \(k\) es impar donde \(k \ge 3\) y \(j = 0\), reescriba $\tan^k x = \tan^{k-2} x \tan^2 x = \tan^{k-2} x (\sec^2 x – 1) = \tan^{k-2} x \sec^2 x – \tan^{k-2} x$. Puede ser necesario repetir este proceso en el término $\tan^{k-2} x$.
4. Si \(k\) es par y \(j\) es impar, entonces use $\tan^2 x = \sec^2 x – 1$ para expresar $\tan^k x$ en términos de $\sec x$. Use integración por partes para integrar potencias impares de $\sec x$. ♦

EJEMPLO ILUSTRATIVO 5.9_8. Integrando ∫tanᴷxsecᴶxdx cuando J es par

Evalúe ∫tan⁶xsec⁴xdx.

Solución:
Como la potencia en secx es par, reescribe sec⁴x = sec²xsec²x y usa sec²x = tan²x + 1 para reescribir el primer sec²x en términos de tanx. Así,

♦

EJEMPLO ILUSTRATIVO 5.9_9. Integrando ∫tanᴷxsecᴶxdx cuando K es impar

Evalúe ∫tan⁵xsec³xdx.

Solución:
Como la potencia en tanx es impar comience reescribiendo tan⁵xsec³x = tan⁴xsec²xsecxtanx. Así,

♦

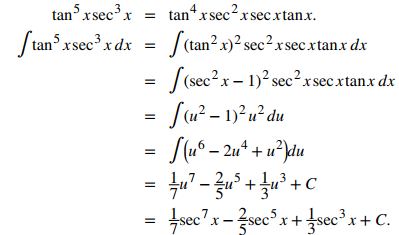EJEMPLO ILUSTRATIVO 5.9_10. Integrando ∫tanᴷxdx donde K es impar y K ≥ 3

Evalúe ∫tan³xdx.

Solución:
Comience reescribiendo tan³x = tanxtan²x = tanx (sec²x − 1) = tanxsec²x − tanx. Así,

♦

EJEMPLO ILUSTRATIVO 5.9_11. Integrando ∫sec³xdx

Integrar ∫sec³xdx.

Solución:
Esta integral requiere integración por partes. Para comenzar, deje u = secx y dv = sec²xdx. Estas opciones hacen du = secxtanx y v = tanx. Así,

Ahora tenemos

Como la integral ∫sec³xdx ha reaparecido en el lado derecho, podemos resolver para ∫sec³xdx agregándola a ambos lados. Al hacerlo, obtenemos

Dividiendo por 2, llegamos a

♦

Ejercicio de control 5.9.8

Evalúe $\int \tan^3 x \sec^7 x \, dx$. ♦

Fórmulas de reducción

La evaluación de ∫secⁿxdx para valores de n donde n es impar requiere integración por partes. Además, también debemos conocer el valor de ∫secⁿ⁻²xdx para evaluar ∫secⁿxdx. La evaluación de ∫tanⁿxdx también requiere poder integrar ∫tanⁿ⁻²xdx. Para facilitar el proceso, podemos derivar y aplicar las siguientes fórmulas de reducción de potencia. Estas reglas nos permiten reemplazar la integral de una potencia de secx o tanx con la integral de una potencia menor de secx o tanx.

REGLA 5.9.2: FÓRMULAS DE REDUCCIÓN PARA ∫secⁿxdx y ∫tanⁿxdx

$\int \sec^n x \, dx = \frac{1}{n-1} \sec^{n-2} x \tan x + \frac{n-2}{n-1} \int \sec^{n-2} x \, dx$

$\int \tan^n x \, dx = \frac{1}{n-1} \tan^{n-1} x – \int \tan^{n-2} x \, dx$

La primera regla de reducción de potencia se puede verificar aplicando la integración por partes. La segunda puede verificarse siguiendo la estrategia descrita para integrar potencias impares de tanx. ♦

EJEMPLO ILUSTRATIVO 5.9_12. Revisando ∫sec³xdx

Aplique una fórmula de reducción para evaluar ∫sec³xdx.

Solución:
Al aplicar la primera fórmula de reducción, obtenemos

♦

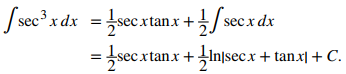EJEMPLO ILUSTRATIVO 5.9_13. Usando una fórmula de reducción

Evalúe ∫tan⁴xdx.

Solución:

Aplicando la fórmula de reducción para ∫tan⁴xdx tenemos

♦

Ejercicio de control 5.9.9

Aplique la fórmula de reducción a $\int \sec^5 x \, dx$. ♦