| 5. La integral y Técnicas de integración | 5.8 Integración por partes |

Ejercicios propuestos para el capítulo 5.8.1

      Al utilizar la técnica de integración por partes, debe elegir cuidadosamente qué expresión es u. Para cada uno de los siguientes problemas, utilice las pautas de esta sección para elegir u. No evalúes las integrales.

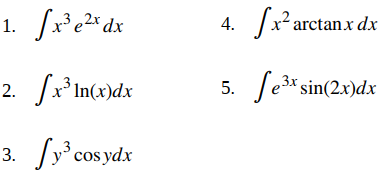
       Encuentra la integral usando el método más simple. No todos los problemas requieren integración por partes.

      Calcule las siguientes integrales definidas. Utilice una utilidad gráfica (o un programa de cálculo simbólico) para confirma tus respuestas:

(Exprese la respuesta en forma exacta).

(Sea u = √x).

41. \(\int_1^e \ln(x^2) \, dx\)

42. \(\int_0^\pi x \cos x \, dx\)

43. \(\int_{-\pi}^\pi x \sin x \, dx\) (Exprese la respuesta en forma exacta).

44. \(\int_0^3 \ln(x^2 + 1) \, dx\) (Exprese la respuesta en forma exacta).

45. \(\int_0^{\pi/2} x^2 \sin x \, dx\) (Exprese la respuesta en forma exacta).

46. \(\int_0^1 x 5^x \, dx\) (Exprese la respuesta utilizando cinco dígitos significativos).

47. Evalúe \(\int \cos x \ln(\sin x) \, dx\)

      Derive las siguientes fórmulas utilizando la técnica de integración por partes. Suponga que n es un número entero positivo. Estas fórmulas se llaman fórmulas de reducción porque el exponente del término x se ha reducido en uno en cada caso. La segunda integral es más sencilla que la integral original:

48. \(\int x^n e^x \, dx = x^n e^x – n \int x^{n-1} e^x \, dx\)

49. \(\int x^n \cos x \, dx = x^n \sin x – n \int x^{n-1} \sin x \, dx\)

50. \(\int x^n \sin x \, dx =\) ______

51. Integre \(\int 2x \sqrt{2x – 3} \, dx\) utilizando dos métodos:

    1. Utilizando la integración por partes, suponiendo que \(dv = \sqrt{2x – 3} \, dx\)

    2. Sustitución, suponiendo que \(u = 2x – 3\)

Indique si utilizaría la integración por partes para evaluar la integral. Si es así, identifique u y dv. Si no es así, describa la técnica utilizada para realizar la integración sin resolver realmente el problema:

52. \(\int x \ln x \, dx\)

53. \(\int \frac{\ln^2 x}{x} \, dx\)

54. \(\int x e^x \, dx\)

55. \(\int x e^{x^2 – 3} \, dx\)

56. \(\int x^2 \sin x \, dx\)

57. \(\int x^2 \sin(3x^3 + 2) \, dx\)

      Dibuja la región delimitada arriba por la curva, el eje x y x = 1, y halla el área de la región. Proporcione la forma exacta o redondee las respuestas al número de decimales indicados:

58. \(y = 2xe^{-x}\) (Aproxime la respuesta a cuatro decimales).

59. \(y = e^{-x}\sin(\pi x)\) (Aproxime la respuesta a cinco decimales).

      Calcule el volumen generado al girar la región delimitada por las curvas dadas alrededor de la línea especificada. Exprese las respuestas de forma exacta o aproximada al número de decimales indicado:

60. \(y = \sin x, y = 0, x = 2\pi, x = 3\pi\) alrededor del eje y (Exprese la respuesta en forma exacta).

61. \(y = e^{-x} y = 0, x = -1 x = 0\); alrededor de \(x = 1\) (Exprese la respuesta en forma exacta).

62. Una partícula que se mueve en línea recta tiene una velocidad de \(v(t) = t^2 e^{-t}\) después de \(t\) segundos. ¿Qué distancia recorre en los primeros 2 segundos? (Asuma que las unidades están en pies y exprese la respuesta en forma exacta).

63. Halle el área bajo el gráfico de \(y = \sec^3 x\) de \(x = 0\) a \(x = 1\). (Redondee la respuesta a dos dígitos significativos).

64. Halle el área entre \(y = (x – 2)e^x\) y el eje x de \(x = 2\) hasta \(x = 5\). (Exprese la respuesta en forma exacta).

65. Halle el área de la región delimitada por la curva \(y = x \cos x\) y el eje x para \(\frac{11\pi}{2} \le x \le \frac{13\pi}{2}\). (Exprese la respuesta en forma exacta).

66. Calcule el volumen del sólido generado cuando se gira la región delimitada por la curva \(y = \ln x\), el eje x y la línea vertical \(x = e^2\) alrededor del eje x. (Exprese la respuesta en forma exacta).

67. Calcule el volumen del sólido generado cuando se gira la región delimitada por la curva \(y = 4 \cos x\) y el eje x, \(\frac{\pi}{2} \le x \le \frac{3\pi}{2}\), alrededor del eje x. (Exprese la respuesta en forma exacta).

68. Calcule el volumen del sólido generado al girar la región del primer cuadrante delimitada por \(y = e^x\) y el eje x, de \(x = 0\) hasta \(x = \ln(7)\), alrededor del eje y. (Exprese la respuesta en forma exacta).